Inscription / Connexion Nouveau Sujet
utilisation de géogebra
Bonjour, j'ai un devoir maison à faire sur geogebra et je suis bloquée dès la première question car je n'arrive pas à tracer la courbe et les points demandés:
Pour a ∈ R, on définit fa :]0; +∞[→ R, x 7→ x(ln(x) + a).
On note Ca la courbe représentative de fa dans le plan muni d'un repère (O;i:j).
On note Sa le point d'intersection de Ca avec l'axe des abscisses.
On note Ea le point d'intersection de Ca avec la droite d'équation y = x.
1. A l'aide de geogebra, formuler une conjecture sur les droites (EaSa)
Merci de votre attention!
J'ai réussi à tracer la fonction mais quand j'essaie de placer le point Sa, celui-ci se place automatiquement sur l'origine du repère au lieu de se placer à l'intersection et je n'arrive pas à le déplacer ..
Bonjour,
Mouais
impossible de s'en sortir, je n'ai pas trouvé non plus
même en forçant une définition de Ca restreinte à x > 0.01 par exemple
et en définissant explicitement S_a = Intersection[C_a,axeX] point final
quand on s'approche de a > un peu, la définition même de S_a est modifiée automatiquement par Geogebra "de lui-même" en
S_a = Intersection[C_a,axeX,(0,0)] et rien à faire pour lui faire changer d'avis
moi j'appelle ça un gros bug de Géogébra, qu'il prennne des initiatives pareilles de modifier la définition d'un point.
La seule solution est de réfléchir à la place de Geogebra et de résoudre soi-même l'équation produit nul x(ln(x)+a) = 0
le seul facteur intéressant étant ln(x) + a = 0, on lui définit Sa comme intersection de l'axe des X avec une autre courbe :
y = ln(x) + a
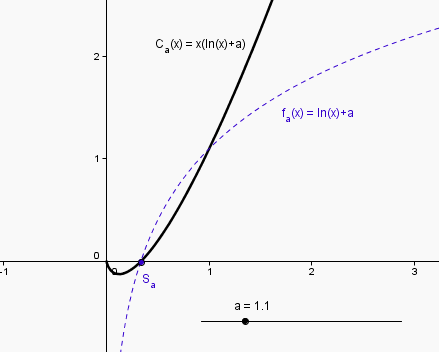
ensuite "pour faire beau" on cache la fonction auxiliaire pour donner l'illusion que Sa est l'intersection de Ca avec l'axe, alors que c'est l'intersection de l'autre courbe (mais c'est évidemment le même point !)
PS : même problème et même solution d'ailleurs pour Ea :
résoudre soi-même l'équation produit nul pour obtenir la seule solution intéressante (celle différente de (0; 0))
étonnant je viens de refaire la figure pour confirmation .... et je n'ai aucun problème ...
je crée ::
le curseur
la fonction f(x) = x(ln(x) + a)
puis intersection de courbes pour les deux points
....
mais j'ai tout de même un bug quand j'anime le curseur :: lorsque les points A (sur (Ox)) et B (sur x = y) arrivent en l'origine ils n'en bougent plus !!!!
cela peut se comprendre puisque il y a deux points d'intersection "si" on prolonge par continuité f en 0 .... ce que geogebra semble faire ....
....
j'ai la version 4.4.8.0 du 14 janvier 2014 ....
une remarque ::
pour le point A je clique sur f et sur l'axe des abscisses ... mais surtout "après" la courbe
si on clique sur l'axe "près" de l'origine ça me renvoie effectivement le msg "non défini" ....
en cliquant sur f et "avant" l'origine ça me retourne "C non défini" et en déplaçant la souris sur le point C ça m'écrit "point C intersection de f et axeX avec (-xxx, -0,01) comme valeur de départ"
il semble qu'il y ait un ordre sous-jacent du plan (ou sur les objets créés (courbe, droite, 0....)) qu'on retrouve d'ailleurs quand on utilise la commande "intersection" (ou l'icone) avec une droite et un cercle ...
to be followed ....

salut,
il est probable qu'on suppose l'utilisateur assez fute pour calculer les coordonnees de E et de S en fonction de a.
Il suffit alors de faire bouger la droite (ES).
il est probable qu'on suppose l'utilisateur assez futé ...
une personne guère plus futé ... voire même moins se passe d'un ordinateur et utilise sa cervelle pour résoudre un problème aussi élémentaire ....
mais vu qu'on a créé des ordinateurs faut bien leur trouver une utilisation ... même quand on en n'a pas besoin ... puisqu'une cervelle même modeste (mais peut-être bien instruite certes (et c'est ce qui fait défaut actuellement)) résout se pb en moins de pas longtemps ...
S = (e-a, 0)
E = (e1 - a, e1-a)
(SE) :: y = 0 + (x - e-a)* e/(e - 1)
de tête bien sur ....

moi aussi ça marche (en cliquant où il faut) mais "quand j'approche les points de l'origine" (c'est à dire quand a devient supérieur à une certaine valeur) Geogebra de lui même change le point de départ de son calcul d'approximation et le met en 0 !!
(tu peux inspecter les propriétés du point et observer ce changement de définition à l'initiative de Geogebra)
donc fatalement ensuite ça reste bloqué à partir de ce départ là, donc sur (0; 0)
tu as donc exactement le même bug avec ton Geogebra 4.4 que moi avec mon 4.0 : Geogebra prend l'initiative de modifier la définition du point.
et donc il faut "bidouiller", par exemple comme j'ai fait
ce qui donne ça (en montrant tout) :
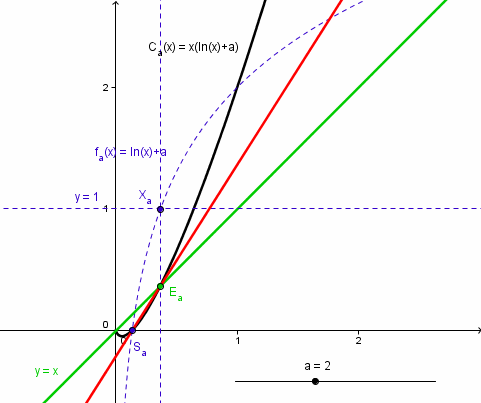
Mes points sont définis par les intersections sans ambiguité de la courbe y = ln(x) + a avec l'axe des x (donne directement le point Sa)
et avec la droite y = 1 (donne un point de même abscisse que Ea, qu'on renvoie en Ea sur la droite y = x)
et ces points Sa et Ea ont alors un comportement parfaitement stable quelle que soit la valeur de a. Ils ne "sautent" jamais en (0; 0)
bon c'est sûr comme déja dit on peut se dispenser de toute cette "expérimentation" et faire le calcul direct qui est effectivement facile, mais c'est bien ici pour satisfaire à ce qui était demandé dans l'énoncé :
1. A l'aide de geogebra, formuler une conjecture sur les droites (EaSa)
Ceux qui n'ont pas Geogebra passent directement à la question suivante et calculent direct, puis font semblant d'avoir utilisé Geogebra en disant "on remarque que" pour cette question "manip expérimentale" qu'ils ne peuvent pas faire.
Heureux hommes qui sont encore incités à penser avant de taper sur des touches...
Si la machine met 3 fois plus de temps pour faire (mal) le boulot, où va-t-on ...
Sur Xcas:
f(x):=x*(ln(x)+a);
sol1:=solve(f(x)=0);
sol2:=solve(f(x)=x);
puis en dessous dans un ecran de geometrie 2-d:
droite(y=x);
a:=element(-10..10);
graphe(f(x));
S:=point(sol1[0],0);
E:=point(sol2[0],sol2[0]);
droite(S,E);
puis en dessous en ligne de commande:
lin(coordonnees(vecteur(S,E))/exp(-a)) // renvoie [exp(1)-1,exp(1)]
Le moteur de calcul formel de geogebra etant le meme que Xcas, on doit pouvoir obtenir qqchose de semblable avec geogebra.
Le moteur de calcul formel de geogebra etant le meme que Xcas
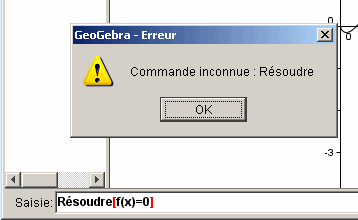
il n'existe pas de fonction Geogebra "Solve"
Racine[C_a, 2] renvoie la racine au point (0; 0), bien qu'on lui ait dit de partir de "suffisemment à droite", du point initial 2.
par contre :
Racine[C_a, 0.001, 2] (ne garder que les racines entre 0.001 et 2) là c'est bon
la fonction Racine marche nettement mieux (= ne prend pas d'initiatives malheureuses) que la fonction Intersection !
mais C_a est toujours "étendue par continuité" au point x = 0
et c'est la seule solution qu'il trouve si on ne lui impose rien.
(il ne donne qu'une seule solution comme résultat de la fonction "Racine", la première qu'il trouve en n'en faisant qu'à sa tête si on ne lui dit rien, la première dans l'intervalle donné si on lui restreint à un intervalle)
la fonction Racines[C_a, 0, 2] donne par contre la seule solution la bonne. allez y comprendre quelque chose ...
c'est en fait pareil avec Xcas etc et tous dans le même sac, entre les différentes fonctions de recherche de solutions (= différentes méthodes, solve n'existe pas, c'est un alias interne qui renvoie vers diverses fonctions qui fonctionnent différemmment) qu'il faut éventuellement forcer pour avoir réellement toutes les solutions ou celle qu'on veut.
voir le mode d'emploi et les drapeaux de Xcas pour forcer la méthode de résolution.
Vu.
j'avais un trop vieux Geogebra
là c'est bon après mise à jour.
(mais pourquoi donc ils ont inversé le sens du zoom ??  )
)
oui mathafou je me doute bien que l'objectif est l'expérimentation informatique .... malheureusement conséquence de la faiblesse de la formation intellectuelle de nos jeunes ... et sans nier l'apport pratique (utile lors de certaines énigmes et dont j'ai profité bien évidemment) ...
ce que je regrette c'est "l'artificialité" de certaines activités pour imposer l'outil informatique ....
d'ailleurs je dois préciser tout de même que ici il apporte tout de même le fait de voir ce qui se passe par la courbe de la fonction ce qui évite son étude pour déterminer ce qui se passe ce qui est aussi un gain de temps et permet de se consacrer à l'essentiel du problème ....
mais cet exercice nous montre aussi qu'il est tout aussi important de connaître les limites ou du moins le fonctionnement de cet outil pour éviter les impasses dans lesquelles on peut tomber ici
ainsi ici deux solutions ::
"cliquer au bon endroit" ... qui relève du coup de bol ...  ... et avec toujours ce bug en l'origine ...
... et avec toujours ce bug en l'origine ...
"forcer la construction" comme le dit si bien mathafou ... et qui est aussi un exercice intellectuel en soit ... mais qui nécessite une certaine maturité et expérience ...
ça me fait penser à cette bonne vielle TI57 (ma première calculatrice en seconde) avec 8 mémoires et 50 pas de programme comme on disait à l'époque ... et le tour de force était d'inverser une matrice 2 x 2 ... une sacrée jonglerie intellectuelle ... d'une grande richesse donc ...

j'ai le meme bug à l'affichage en geometrie dynamique avec Xcas, mais les coordonnees des points sont exactes.
Je poste le pb à bernard parisse (developpeur de giac/Xcas).
remarque que avec la fonction calcul symbolique Résoudre, et ensuite en affichant le point obtenu et en l'appelant S_a c'est nickel .
c'est juste la fonction "Intersection" qui est buggée.
bon j'ai plus de problème en faisant comme ceci
une remarque préliminaire :: si deux "objets" ont plusieurs points d'intersection geogebra ne les affichent tous que dans certains cas particuliers voir mode d'emploi ...
pour en revenir au pb ici :
lorsque qu'on clique point d'intersection de f et l'axe x (en cliquant dessus) ou de f et {y = x} ça bugue ...
j'ai donc créé les fonctions g(x) = 0 et h(x) = x
puis j'ensuite j'utilise la commande intersection["fonction", "fonction", xmin, xmax]
je rentre alors f, g ou f, h puis -1 et 10abs(a) pour les bornes
cette fois ci lorsque j'anime mon curseur tout marche (avec parfois des "non défini" suivant les valeurs de a) mais tout marche ....

oui mathafou :: à vouloir proposer plusieurs possibilités pour la commande "intersection" on perd de la souplesse (n'affiche donc pas toujours tous les points (sauf quand il reconnaît des coniques ou des polynômes)) et induit un "ordre" des points d'intersection ....
faut donc bien connaître le mode d'emploi ....