Inscription / Connexion Nouveau Sujet
valeur d'un angle après projection orthogonale
Bonjour à tous,
pour la construction d'un dôme géodésique, je dois fabriquer des pièces qui permettront de raccorder les arêtes d'une pyramide à base hexagonale non régulière.
Je connais les angles entre les arêtes dans leurs plans respectifs (tous différents), mais j'ai besoin de calculer la valeur de la projection orthogonale de ces angles sur le plan constitué par la base de la pyramide.
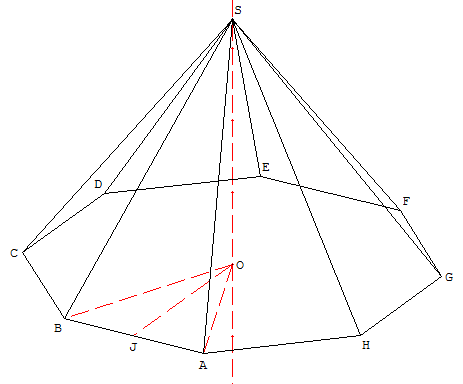
Voilà un exemple du problème (avec une pyramide à base octogonale, mais je pense que le problème est le même).
Dans mon cas, je dispose par exemple de la valeur de l'angle ASB, et je voudrais pouvoir calculer sa projection orthogonale dans le plan de la base : l'angle AOB.
Ma construction impose, les angles OSA.
Je ne sais pas trop comment aborder le problème et mes souvenirs de trigo ou de calcul vectoriel commencent à remonter loin, maintenant. Merci pour vos lumières.
PS : à l'attention des modérateurs : comme il s'agit d'un problème à caractère non scolaire, je voulais poster dans "Autre", mais les thèmes proposés ne convenaient pas. Merci de déplacer ce fil, s'il n'est pas à la bonne place.
Bonjour ,
Es-tu sûr que tu ne connais que les 2 angles ASB et OSA ?
Tu n'as aucune autre dimension comme OS ou SA ou ...
Cordialement
bonjour,
autre question: Bien que non régulière, les sommets de la base de ta pyramide sont-ils cocycliques ?
Je ne suis pas sûr de pouvoir calculer SA. Peut-on faire sans ?
Les points de la base seront cocycliques.
Voilà un exemple de platine de raccordement comme je voudrais en fabriquer.
Malheureusement, les mesures des angles que j'ai trouvées correspondent aux angles entre les arêtes, et il y a de nombreux angles particuliers (porte, coplanéité de tous les sommets assurant la base du dôme).
Merci.
>Y a t'il un lien entre les 2 figures ?
La photo est l'exemple concret de ce que je voudrais réaliser :
les plaques en bois hexagonales correspondent au plan de la base de la pyramide. Les arêtes se rejoignent, au sommet de pyramides non régulières.
J'ai les données des angles entre les arêtes, mais je cherche les valeurs des projections de ces angles sur les plaques en bois, pour pouvoir percer les plaques perpendiculairement et pouvoir assembler le tout (montant percés également).
J'ai l'impression que mon schéma du début modélise correctement la situation, me tromperais-je ?
Oui c'est assez bien modélisé quoiqu'un peu plus pointu . Ne connait'on aucune autre longueur , diamètre , ... en plus des 2 angles ?
Je peux fixer OA : il sera égal au rayon de chaque platine de raccordement.
rayon OA=10cm.
angle axial OSA = variable de 78° à 80°. Qu'il reste sous forme de paramètre
angle ASB = variable de 55° à 63°. Qu'il reste sous forme de paramètre
Du coup, OS = OA. tan-1OSA, mais ça ne m'aide toujours pas
Merci pour vos réponses
Je m'auto cite :
>Du coup, OS = OA. tan-1OSA, mais ça ne m'aide toujours pas
Je ne suis plus sûr de mon écriture, je veux dire : OS = OA.(tan OSA)-1
Merci pour ta réponse, mais j'ai l'impression qu'il y a une méprise.
Les points O,A,B forment un plan différent du plan formé par A,S,B.
L'angle ASB est tel que 55  angle ASB
angle ASB  63
63
Je cherche la valeur de la projection orthogonale AOB de ce angle. O étant le projeté de S.
La somme des 6 angles projetés, AOB, BOC, COD ... doit être égale à 360°.
Merci.
J'ai simplement fait une mise à plat (autour de SA) pour montrer les calculs qu'on peut faire .
La valeur de l'angle AOB est obtenue par la formule tan (AOB/2) = AJ / OJ donc AOB = 2 Atan (AJ/OJ)
Les formules sur la figure donnent AJ et OJ .
Connaissant les 2 angles OSA et ASB qu'on peut faire varier avec les curseurs GeoGebra , et la longueur OA (qu'on pourrait faire varier pareillement) , on obtient l'angle AOB en affichant le résultat du calcul donné précédemment .
Je ne suis plus sûr de mon écriture, je veux dire : OS = OA.(tan OSA)-1
OS = OA tan (
 /2 - OSA)
/2 - OSA)Merci pour ta réponse.
Je n'avais pas pensé à faire figurer B dans le plan (OAS). Ça devrait me permettre d'avancer.


 géométrie en post-bac
géométrie en post-bac