Inscription / Connexion Nouveau Sujet
Variable aléatoire
Bonjour voici l'exercice de mon DM, Pourriez vous m'aider s'il vous plaît. 
Une industrie alimentaire produit des boules enrobées de chocolats de différentes couleurs. Le responsable de fabrication annonce que la proportion p de boules rouges ou jaunes, présentes dans la production, est égale à 0.36. On tire au hasard et avec remise un échantillon de n boules dans la production. On note Xn le nombre de boules rouges ou jaunes présentées dans cet échantillon.
1)a. Quelle est la loi suivie par a variable aléatoire Xn. Justifier et préciser les paramètres.
b. Soit Fn la variable aléatoire définie par Fn = . Que représente le nombre Fn pour un échantillon prélevé de n boules ?
On s'intéresse dans la suite, à la probabilité que Fn appartiennent à l'intervalle
In = [p-1.96 ; p+1.96
] pour différentes valeur de n.
2)Dans cette question n=100
a. Déterminer l'intervalle I100 ( arrondir les bornes à 10-4 près)
b.Montrer que a probabilité que F100 appartienne à l'intervalle I100 est égale à la probabilité P(27
X10045) et en déterminer une valeur approchée à 10-3
| n | b1 = p - 1.96 | b2 = p + 1.96 | a | b | p( In) |
| 100 | 27 | 45 | |||
| 110 | |||||
| 120 |
4) On souhaite augmenter la taille n de l'échantillon. Pour cela, on automatise les calculs sur tableur.
a) Réaliser la feuille de calculs ci-dessus jusqu'à n = 2000.
b) Représenter P(
In) en fonction de n sous forme d'un nuage de points.
c) Quelle conjecture peut-on faire sur la probabilité P (
In)
On dit que In = [p-1.96
5) On définit pour n
100, la variable aléatoire Zn =où E(Xn) et
(Xn) désignent l'espérance et l'écart type de Xn.
a. Déterminer les bornes de l'intervalle de fluctuation In en fontion de n.
b. Démontrer que
In équivaut à -1.96 Zn 1.96.
c) Justifier à l'aide d'un théorèmeque
In) = 6) Comparer pour quelques valeurs de n, l'intervalle In avec l'intervalle Jn de fluctuation au seuil de 95% introduit en classe de seconde : lorsque n
25 et 0.2p0.8 Jn= [p-7) On s'interroge sur la proportion p=0.36 de boules rouges ou jaunes annoncées par le responsable de fabrication.
On décide de prélever 200 boules au hasard et avec remise dans la production. Dans cet échantillon, 62 sont rouges ou jaunes.
Peut-on accepter l'hypothèse selon laquelle la production contienne effectivement 36% de boules rouges ou jaunes ? Justifier.
Voila je pense n'avoir rien oublier.
Merci
J'ai répondu à la première :
1.a. La variable aléatoire Xn suit une loi binomiale de façon aléatoire et avec remise. Les paramètres présents sont p et n. Ainsi Xn suit B ( 0.36 ; n )
Ensuite pour la 2.
Fn = \frac{Xn}{n}. Xn -> nombre totale de boules rouges ou jaunes.
n -> le tirage aléatoire de boules
Donc Fn est la probabilité qu'on puisse tirer une boules rouges ou jaunes.
Ici je ne suis pas sûre. 
salut
Une industrie alimentaire produit des boules enrobées de chocolats de différentes couleurs.
si les boule sont enrobées de chocololat ..avoir du jaune ou du rouge ..comment ?
ou alors l'enonvé veut dire avant enrobage
..Xn suit une loi binomiale de parametre B(n;0,36) et Fn = Xn/n représente la proportion de boules rouges ou jaunes
Bonjour flight,
Oui je sais ça parait bizarre mais bon ce n'est qu'un énoncé ... 
----------
D'accord ensuite pour la 2.a. j'ai mis le réponse précédemment et arrivé à la 2.b. c'est ici que je bloque.
Merci
re... pour ton intervalle I100 ta réponse de 12h44 est bizarre l'intervalle
I100[0,26592 ; 0,455408] donc 0,26592Fn/100 ;0,455408] soit aussi 26,59Fn45,54 les valeurs de l'enoncé s'en approchent
3.
| n | b1 = p - 1.96 | b1 = p + 1.96 | a | b | p( |
| 100 | 0.26592 | 0.45408 | 27 | 45 | 0,953 |
| 110 | 0,2703 | 0,4497 | 30 | 49 | 0,954 |
| 120 | 0,2741 | 0,4459 | 33 | 53 | 0,954 |
PS : J'ai tout arrondi
Merci
Alors pour la 4.
J'ai fait tout ce qui est demandé mais je trouve que le nuage de point est très bizarre.
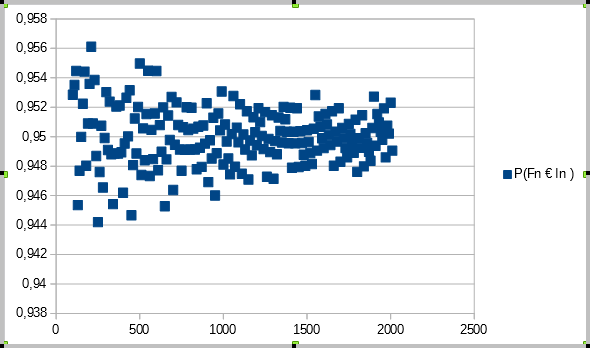
Bon je continue
pour la 4.c.
Le conjecture est que la prob que Xn/n appartient à In est comprise environ entre [0.944 ; 0.56]
Salut flight ravie de de revoir,
Non je suis bloquée, est ce que mes réponses précédentes sont exacts ?
Merci
un coup de pouce
comme on a etablit que :
p - 1,96
(p(1-p)/n)Xn/np + 1,96(p(1-p)/n)
alors n.p - 1,96(np(1-p))Xnnp + 1,96(np(1-p)).
comme Z = (Xn - n.p)/ car E(Xn)=n.p
alors en remplacant Xn dans l'inegalité par Zn + n.p il reste
-1,96Zn1.96
Par contre pour le théorème ... Je n'ai pas compris en cours donc l'appliquer ici je ne sais pas c'est lequel ....
..de toute facon P(Xn/n In) doit etre de 0,95 et l'expression qu'on trouve apres l'egalité c'est celle de la loi normale dont la variable aleatoire et Zn d'esperance 0 et d'ecart type 1
le calcul de l'integrale est simplement 
1,96)- (-1,96) = 2(1,96) - 1 = 2*0,9750 -1 = 0,95 (resultat attendu)
..pour affirmer que la production contient effectivement 36% de boules rouges ou jaunes avec une certitude de 95%
Merci pour les aides mais la 5.a.
Pour déterminer les bornes de l'intervalle In en fonction de n ? Je ne sais pas si on la faite...
Annuler
connectez vous