Inscription / Connexion Nouveau Sujet
variations fonction
bonjour voici la consigne
Etudier les variations de la fonction f définie sur [0;1] par f(x) = ln(1+ex) - x - 1/e
En déduire que, pour tout x  [0;1] : ln(1+ex)
[0;1] : ln(1+ex)  x + 1/e
x + 1/e
Donc j'espère que déjà ex = e^(x)
je trouve f'(x) = 1
donc f(x) strictement croissante sur I
mais je bloque à la deuxième question pourriez vous m'aider svp 
merci
ah non en fait ex c'est ku ici donc je trouve f'(x) = e-1 mais pour trouver les variations c'est plus compliqué..
Bonjour,
Il faut utiliser la formule qui donne la dérivée de ln u .
Je ne vois pas pourquoi ex serait ex . Si c'est écrit ex dans l'énoncé, c'est le produit de e par x .
Où avez-vous lu que j'avais écrit ?
il faudrait faire attention
pas de problème, je vais continuer bonne nuit Sylvieg
ben j'ai mis sur le même dénominateur
f'(x) = e/(1+ex) -(1+ex)/(1+ex)
(e-1-ex)/(1+ex)
et là je bloque..
je vais aller dormir je pense tant pis j'arrive plus à réfléchir
vraiment désolé et merci pour votre aide, si vous pouviez juste me donner une indication pour la deuxième partie de l'exo, j'essaierai de comprendre demain
merci quand même bonne nuit ..
bien on continue
signe de
on peut «supprimer» le dénominateur car strictement positif
le signe de est donc celui de
calcul du maximum et utilisation de celui-ci
cela revient à montrer que
ce qui ce déduit directement de la question précédente vu la valeur du maximum
ah je dois juste faire le maximum (càd remplacer x par un au numérateur ?) et non pas résoudre e - 1 -ex > 0
Bonjour,
Je suis réveillée !
Pourquoi remplacer x par 1 ?
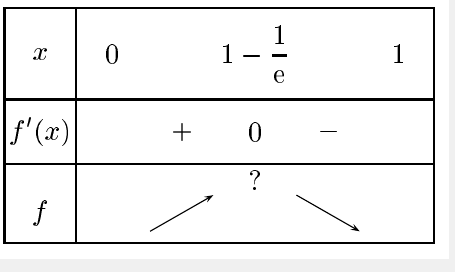
Signe de :
Le dénominateur est positif car 0
 x
x 1
1
Il reste à étudier le signe du numérateur e-1-ex .
Il est nul pour x = (e-1)/e = 1-1/e qui est bien compris entre 0 et 1.
Tu es censé connaître le signe de ax+b . Ici a = -e ; donc e-1-ex est positif avant 1-1/e, et négatif ensuite.
D'où le maximum pour x = 1-1/e .