Inscription / Connexion Nouveau Sujet
Vecteur et rectangle
Bonjour,
Je suis ici pour trouver de l'aide et comprendre comment aborder un problème comme celui-ci j'espère que vous pourrez m'aider.
Voici l'énoncé :
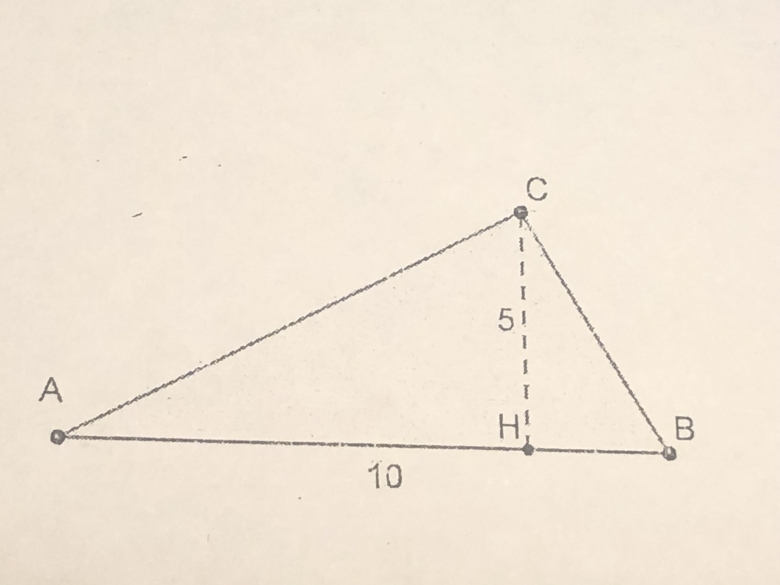
« Dans le triangle ABC (photo si dessous), on sait que AB=10 et que CH=5 (H est le pied de la hauteur issue de C). Determiner la position H sur [AB] pour que le triangle ABC soit cette fois rectangle en C. »
J'ai essayé d'utiliser le théorème de Chasles mais il n'est pas utile ici ; toutes mes tentatives étaient vaines puisque nous n'avons pas les valeur nécessaires pour la trigonométrie où Pythagore et même Thalès. Je suis perdue et après avoir consacré bien du temps à ce problème je m'en réfère à vous.
Merci de votre attention, je vous souhaite un tres bonne journée.
Bonjour,
Le produit scalaire est au programme de seconde maintenant ?
On peut utiliser Pythagore.
La position du point H sur [AB] est déterminée par la donnée d'une des longueurs AH ou BH.
Pour démarrer, je conseille de poser x = AH ou BH selon son humeur.
Choisir une inconnue permet d'avancer avec Pythagore dans les trois triangles rectangles de la figure.
PS On peut aussi deviner la réponse quand on pratique depuis longtemps les triangles rectangles isocèles 
Bonjour Sylvieg
le problème est le titre !
la seule façon de résoudre en utilisant les vecteurs est le produit scalaire et Chasles.
le demandeur est-il en France ? vu l'heure de la demande on peut sérieusement en douter, donc programme peut être différent.
(d'ailleurs c'est plus direct si on développe )
parce que sans les vecteurs c'est instantané avec la géométrie de collège en pensant "constructions géométriques" :
un triangle rectangle est inscrit dans un cercle de diamètre l'hypoténuse, et c'est terminé.
(et avec ces valeurs même pas besoin de calculs ni d'équation)
Bonjour,
Merci de votre réponse ; cependant nous n'avons pas étudié le produit scalaire (mais il est vrai que nous devons résoudre le calcul avec des vecteurs). Je ne comprend donc pas la formule (CA.CB ) car notre professeur ne nous a pas parlé du signe « . » en calcul.
Je vais chercher son sens.
Merci beaucoup pour votre aide, je vous souhaite une très bonne journée !
Bonsoir
si tu cherches ce que signifie le . entre les deux vecteurs, tu vas tomber sur la notion de produit scalaire de vecteurs que tu n'as pas étudiée...donc à mon avis, évite cette méthode
Prends un chemin à ta portée, avec tes connaissances, comme conseillé par exemple par Sylvieg...
moi je laisserais tomber cette histoire de vecteurs...je crains entendre la correction d'ici...ah j'avais cru qu'on pouvait utiliser les vecteurs , mais non, pas ici

Bonjour,
ceci dit aucune suite n'est donnée par le demandeur ...
il attend sans doute la correction ...
la piste de Sylvieg conduit à une équation du second degré
Certes ici elle se simplifie car une solution double, mais tout de même...
Si par exemple on avait eu CH = 4 on aurait eu les deux solutions AH = 8 et AH = 2, solutions de x² - 10x + 16 = 0,
équation obtenue par l'application de Pythagore dans les trois triangles rectangles,
ou plus directement par le fait que les triangles AHC et CHB sont semblables.
on obtient d'ailleurs la même équation par les produits scalaires car ils conduisent aussi à la même relation générale HA  HB = HC² (en longueurs), valable dans tout triangle rectangle ...
HB = HC² (en longueurs), valable dans tout triangle rectangle ...
il fut un temps où cette relation, était dans le cours ...
("relations métriques dans le triangle rectangle")
la mienne (cercle circonscrit) donne directement le(s) position(s) par une seule application directe de Pythagore, sans équations.
Dans le bon triangle, un qui n'est pas tracé sur la figure de départ...


