Inscription / Connexion Nouveau Sujet
Vecteurs et repères
Bonjour
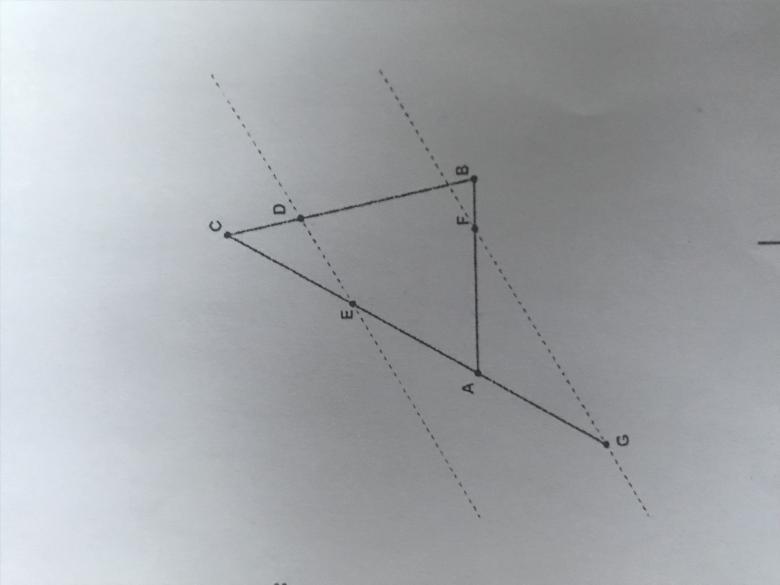
Dans un triangle ABC, on considère les points D, E, F et G définis respectivement par :
CD= 3/10CB
E milieu de AC
AF= 3/4AB
G est le symétrique de E par rapport à A
on souhaite démontrer que ED et FG sont parallèles.
Dans le repère (A,B,C), déterminer les coordonnés des points de la figure et conclure
Ce j'ai fais :
J'ai trouver quelques coordonnés
A(0;0). B(1;0). C(0;1). E(0;1/2). G(0;-1/2)
Il me reste à trouver les coordonnés du point D mais je pas du tout comment avoir ses coordonnés
Merci de m'aider
non attention 1-0=1
vous en faites autant avec
comme d'habitude on prend
on écrit les égalités et on résout
ED = (xd-xe|yd-ye) = (3/10|1/5)
FG = (xg-xf|yg-yf) = (-3/4|-1/2)
Je pense que j'ai faux vu que quand je calcule avec la formule det(ED,FG) = (3/10) x (-3/4) - (1/5) x (-1/2) je ne trouve pas cela égal à 0


