Salut,
Bizarre comme question. Le problème de la sphère est que la vitesse sera maximal à l'équateur et nulle sur les pôles. Donc tu veux calculer la vitesse à quel endroit exactement ? de tout les point sur la sphère ?

Bonjour,

Il faut peut-être revenir à la définition de la vitesse de rotation d'une sphère !

Que doit-on mesurer ?  

Que doit-on calculer ?  

bonjour,
J'aimerais que tu répondes à trois questions.
1. Est-ce que le centre de ta sphère est fixe ?
2. Puisque tu parles de position moyenne de l'axe de rotation, cela signifie que la sphère oscille et qu'à chaque couple ,le deuxième étant l'image du premier après rotation, tu sais déterminer la position de l'axe correspondant de rotation. Comment fais-tu  ? Pour moi avec deux points sur une sphère, en supposant déjà que son centre soit  fixe, l'axe correspondant est inclus dans le plan médiateur de , mais c'est tout...
3. Quand tu observes deux points associés, le point en question a-t-il fait moins d'un tour ou plusieurs tours ? (car 1 minute c'est long..)

Supposons résolue cette question. Avec la position de l'axe , tu peux retrouver la latitude des deux points , donc le rayon du parallèle passant par les deux points, tu appelles H le centre de ce parallèle situé donc sur l'axe de rotation,  dans le cas d'un temps court dt , on pose

Un calcul simple te permet d'exprimer en fonction de
la vitesse angulaire de la sphère est

Bonjour,

Merci pour vos réponses.

je souhaite connaitre à quelle vitesse angulaire la sphère se déplace (angle/min). Par exemple, si ma sphère fait un tour en 24 h, je souhaiterais calculer 0.5 dg/min.

1. Le centre est supposé fixe. Je dit supposé car les points ne sont, à la base, pas tous exactement sur la sphère (légères variations). Mais c'est dur de savoir si cela est du à un mouvement du centre ou à des erreurs d'enregistrements (basé sur l'enregistrement du champ magnétique). Je projette donc tous les points dessus la sphère et part de l'hypothèse que le centre est fixe (partons déja du problème le plus simple ).

2. Pour l'instant j'utilise l'algorithm de Kabsch en prenant un certain nombre de points (environ 100) pour déterminer l'axe de rotation sur cet ensemble de points par les moindres carrés. J'ai également vu qu'on pouvait faire le produit vectoriel de OA, OB (O = centre et A, B 2 points). Mais je ne sais pas si cela est correct. J'ai des fichiers de référence ou la vitesse est connue, je pourrais peut être vérifier cela en calculant un angle différent de <AOB.

Si mon axe est dans le plan médiateur de mes 2 vecteurs, il ne passe pas forcement par zéro ? Sur une sphère en rotation, l'axe de rotation ne doit il pas passer par zéro et le pole Eulérien ?

3. ça tourne très lentement, de 1-2 degrés par minutes en général (d'apres l'estimation de mes précédents calculs).

Désolé pour le double post, c'est pour montrer mon avancement dans le problème.

J'ai essayé 2 techniques, une basée sur le produit vectoriel à partir de 2 points et l'autre sur les plan médiateurs en prenant 3/4 points. La première méthode (trouvé sur un forum) ne marche que si je connais le centre de rotation (si je prends l'origine comme centre, ça ne marche que pour des points vers l'équateur). Je ne comprends pas ce qui cloche dans le calcul de la seconde ...

Pour la seconde méthode (trouvé dans Geometric design of linkage), on prends 2 points (p et q) et leur position respectives après rotation (P et Q). L'axe de rotation est à l'intersection des 2 plans médiateurs :

et . On a la solution Y=S donnée par : .

A partir de là on déduit l'angle, avec S, x = points avant rotation, X = point après rotation :

Disons que j'ai les données suivantes :
Longitude : P1=pi/4, P2=2*pi/4, P3=3*pi/4, P4=pi
Colatitude : P1=P2=P3=0.05

ce qui fait en coordonnées cartésiennes :
P1_x=3.534061e-02  P2_x=3.060240e-18 P3_x=-3.534061e-02 P4_x-4.997917e-02
P1_y=3.534061e-02  P2_y=4.997917e-02  P3_y=3.534061e-02  P4_y=6.120481e-18
P1_z=P2_z=P3_z=P4_z=0.9987503

Je veux calculer l'axe (ou le pole eulerien) et l'angle (théoriquement, axe = c(0,0,1) et angle = 45 degrés).

Disons que p=P_1; P=P_2; q=P_2; Q=P_3

P-p=(-0.03534061,  0.01463856,  0.00000000)
Q-q=(-0.03534061, -0.01463856,  0.00000000)
Ce qui donne S=(0.9855986; -0.1691020; 0.0000000)
donc pas mon axe attendu ..., j'ai S=(0.7071068 -0.7071068  0.0000000) si je prends  p=P_1; P=P_2; q=P_3; Q=P_4.

Je ne comprends pas ce calcul... si tous mes points sont sur le même parallèle, je ne peux pas avoir un axe de rotation en (0,0,1) ?

Par contre, si j'utilise S=(0,0,1) pour le calcul de mon angle, j'obtiens le bon résultat.

Quelqu'un voit-il une erreur dans mes calculs, une explication ?

Méthode 1 : Y'a t-il un moyen de trouver le centre de rotation ? (à partir de la colatitude ?)

Bonjour,
désolé de répondre si tardivement.
Dans ma réponse, je considère toujours deux points p et P son image, J'avais en effet considéré qu'ils n'étaient pas sur l'équateur, donc d'un point de vue géométriquement simple (centre fixe et axe stable durant un temps très court, il est clair que le produit vectoriel ne fournit absolument pas l'axe, l'axe est dans le plan médiateur de et il fait un angle de avec   où    est la latitude commune des points et .
pour avoir l'axe il faut déterminer l'image de    par la rotation dans l'espace orienté (orientation naturelle) d'axe orthogonal au plan médiateur et d'angle  

Maintenant, toujours en considérant le système stable, si tu as deux couples de points homologues et , dans ce cas l'axe est l'intersection des plans médiateurs.

Mais ceci ne semble pas répondre à ton problème, puisque tu dis que ton axe est déterminé statistiquement.

Pour la vitesse angulaire, tu fais comme je te l'ai indiqué succintement, (il te faut l'angle où H est la projection orthogonale commune de et de sur l'axe de rotation, celui que j'ai noté )

Merci DOMOREA, ça ne marche pas encore (sauf si latitude=0 et pi/4) mais
je persévère!
J'ai du faire une erreur quelque part car mon angle varie en fonction de
la colatitude ... Je vais détailler mes calculs pour être sûr qu'il n'y
a pas de problèmes.

Avant cela, j'ai une première question :
Si mes 2 points P,p ne sont pas sur la même latitude,
correspond t-il à la moyenne de mes latitudes ?

Je vais prendre ces points comme exemple et qui correspondent à des
longitudes de et et à une colatitude
commune de puis et
qui possèdent les mêmes longitudes et la
latitude commune

produit vectoriel :
Résultat 1 :
Résultat 2 :

Plan médiateur: Je trouve , l'équation de mon
plan médiateur M correspond à . Si
j'obtiens , la normale au plan correspond à
, qui me servira d'axe de rotation.
Résultat 1 :
Résultat 2 :

Mon angle de rotation est -alpha. J'utilise la matrice de rotation
suivante, avec S mon axe : avec et
.

Alpha 1 :
Alpha 2 :

Résultat axe normalisé 1 :
maisen utilisant alpha
et non -alpha.
Résultat axe 2
:eten
utilisant alpha et non -alpha.

Une fois que j'ai mon axe , je projette p et P sur mon axe S
pour obtenir H avec .

H1= sinon avec
alpha
H2= sinon avec alpha


Je calcule l'angle avec en calculant hp et HP.

Angle1 = 45 degrés avec alpha ou -alpha
Angle2 = 23.76 et 23.76 degrés

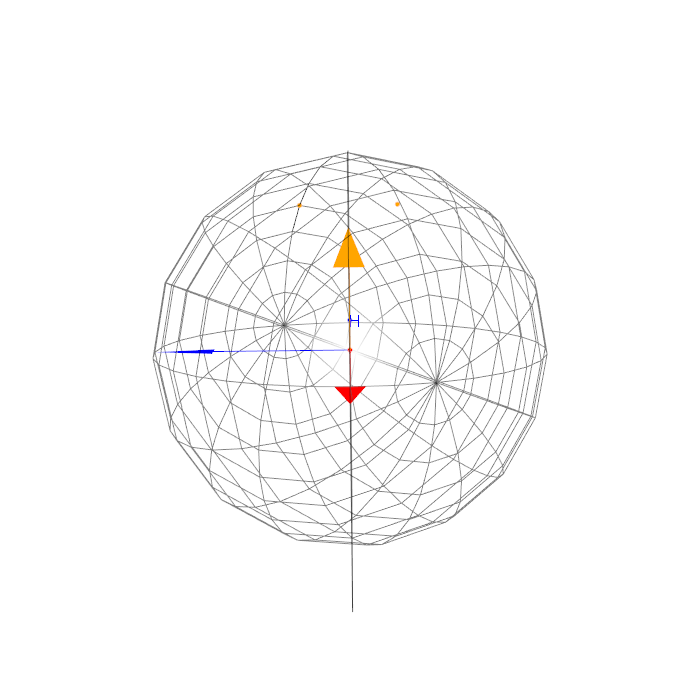
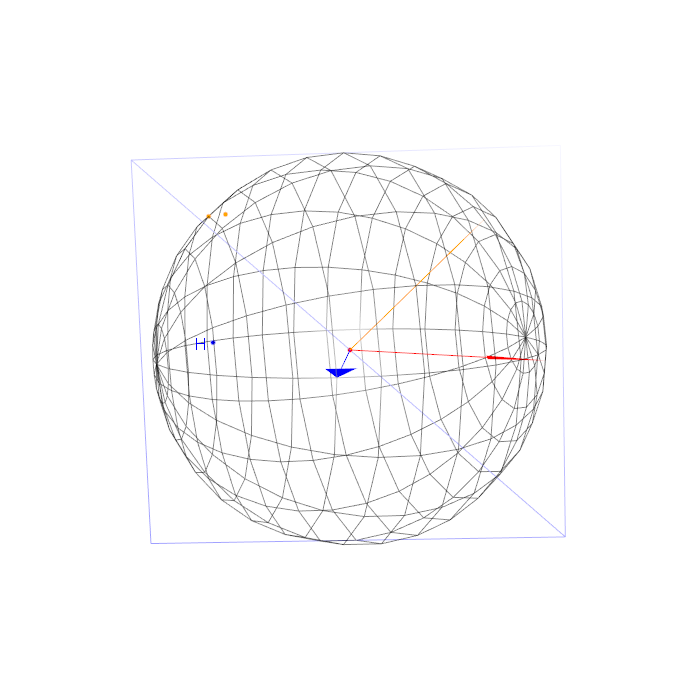
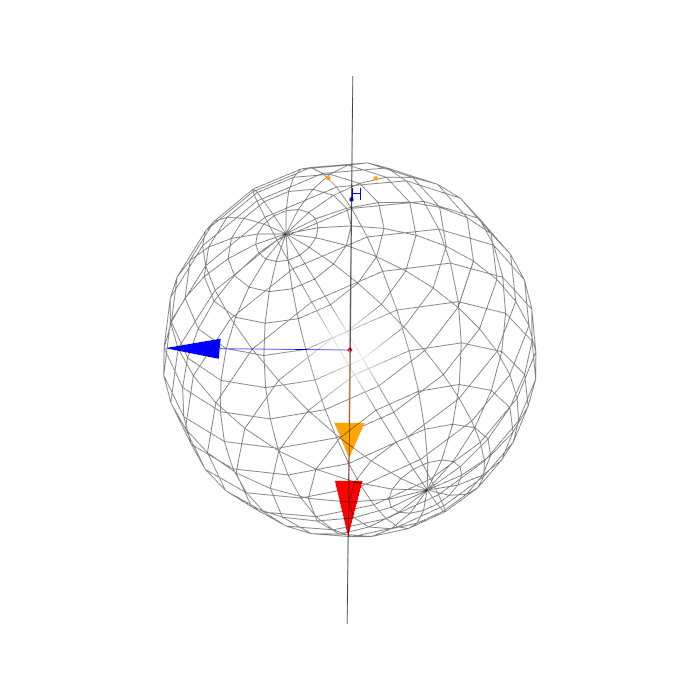
Graphiquement, résultat 1 = 2 premières figures, résultat 2 = 3e figure,
le plan médiateur est représenté par le rectangle bleu, la normale par
la flèche bleue, le produit vectoriel par la flèche jaune, en rouge mon
axe, points jaunes = p et P, point bleu =H et point rouge =origine. Mon
axe est tout le temps dans le plan médiateur (si jamais on ne le voit
pas bien).

Bonjour, je suis toujours bloqué au même niveau, je ne trouve pas mon erreur ci-dessus ça serait bien si je solutionnais ça car cela semble être vraiment ce qui colle le mieux à mes données.

En attendant j'ai essayé la méthode basée sur 3 points (intersection des plans médiateurs) puis j'ai simulé de nouvelles données avec mes axes et angles calculés. ça colle assez bien à la forme globale de mon mouvement sur la surface de la sphere, traduisant je pense une vitesse moyenne correcte, mais la vitesse pour chaque minute n'est pas toujours très précise (parfois des écarts entre les points théoriques et observés).