bonjour

déjà je dirai que si elle est ouverte, c'est plutôt au-dessus et que ça doit être bl qui n'est pas multiplié par 2

bref, tu appelles S(b;l) sa surface en la ramenant à seulement 2 variables puisqu'on connait son volume (donc tu remplaces a)

et tu cherche le minimum de cette fonction de deux variables

Autant pour moi MatheuxMatou, je me suis trompé en recopiant.

Je vais essayer ça, merci beaucoup !

Bon, récapitulons :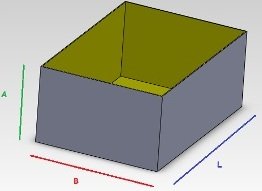

Equation de la surface : S= 2AB + 2AL + BL
Volume : 32m3 = A.B.L d'où A = 32/(B.L)

On remplace A dans S : S= 64/L + 64/B + B.L

Ensuite recherche des points critiques : là je tourne en rond..

Autre piste : on sait que la plus petite surface pour contenir un volume est une sphère, de même si on veut un parallélépipède, la plus petite surface serait obtenue par un cube! Mais dans notre cas le couvercle étant ouvert je ne crois pas que ça marche..

comment fais-tu pour trouver les points minimaux ?

Je cherche d'abord les points critiques que je n'arrive pas à trouver. Enfin ça me donne quelque chose comme 4.16999x10^-5...

Ensuite dérivées secondes partielles par rapport à B et L que j'appelle R et T

Puis dérivée par rapport à B de la dérivée par rapport à L que j'appelle S

--> si RT - S² > 0 et si R > 0 alors le point critique que j'ai trouvé est le minimum..

tu montres ce que tu as fait oui ?

f(B;L) = 64/L + 64/B + B.L

f'(B) = -64/B² + L
f'(L) = -64/L² + B

Point critique <=> { L = 0
                   { B = 0  (c'est juste ?)

f"(B) = 128/B^3
f"(L) = 128/L^3
f"(B;L) = 1

R = 0
T = 0
S = 0

RT - S² = 0


------> FAUX !! ça ne me parait pas très utile tous ces calculs..

n'importe quoi !

fonction non définie pour B=L=0

tu ne sais pas résoudre f'(B)=f'(L)=0 ?

D'un côté, c'est pas parce qu'on est sur îlemaths.net qu'on est bon en maths..

Bon si je résous cette équation :

f'(B)=f'(L)=0 <=> -64/B² + L = 0 & -64/L² + B = 0

Ca me donne L = 64/B² & B = 64/L²   on peut enlever le carrée : √L = 8/B & √B = 8/L

Mais je ne vois pas quoi faire avec cela

effectivement ! mais tu es en IUT de quoi ???? et tu as un bac quoi ????

BL²=LB²=64

(c'est vraiment que quand on est "pas bon en math", c'est mieux de travailler avec la racine carrée !!!)

première égalité B=L

et en remplaçant B=L=4

Oué oué je vois maintenant !

C'est pas que je suis nul en maths mais des fois ça ne me vient pas.
J'ai un bac s-si (sans option math je te rassure) et je suis en 2eme année de dut génie mécanique.

Je pense que ce qui ma perturbé c'est de ne pas avoir de point critique, je veux dire que d'habitude on a toujours des equations du style 2x = 0 et y = 0..

En tout cas merci à toi