Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Autre GéométrieTopics traitant de géométrie [tout]Lister tous les topics de mathématiques
Niveau autre
Partager :

Volume d'une cuve à fonds GRC

Posté par
LePec 29-04-13 à 16:54

Bonjour à tous,

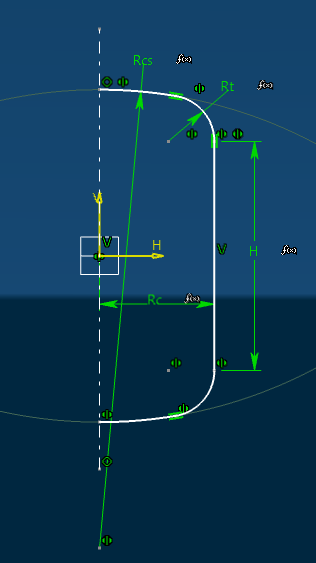
Je suis actuellement entrain de réaliser un projet qui consiste à simplifier les commandes clients de réservoirs sous pressions à fonds GRC. Les fonds GRC (ou fonds bombés à Grand Rayon de Carré), sont des fonds torisphérique composés d'une calotte sphérique, d'un élément torique appelé carré et d'un corps cylindrique, tous trois tangents les uns aux autres.
Ci-joint une esquisse de la figure concernée avec son axe de révolution.

Relations:
Rc = H/2
Rcs = 2*H
Rt = 0.1*R

Je dois déterminer une formule du volume total du réservoir, dépendant de ces 4 facteurs (H;Rc;Rt;Rcs). Avez vous une idée de comment s'y prendre?
Merci par avance.

Volume d\'une cuve à fonds GRC

Posté par
GaBuZoMeure : Volume d'une cuve à fonds GRC 29-04-13 à 17:18

Vu que Rc, Rcs et Rt dépendent de H, en fait le volume ne dépend que de H, non ?

Posté par
GaBuZoMeure : Volume d'une cuve à fonds GRC 29-04-13 à 17:27

J'avais lu Rt=0,1*H. Mais si c'est Rt=0,1*R, qui est ce R ?

Posté par
LePecre : Volume d'une cuve à fonds GRC 29-04-13 à 17:35

Oui c'est ca. L'idée est de définir la géométrie du réservoir pour un volume donné. Compte tenu des relations, exprimer le volume en fonction de H.

Posté par
LePecre : Volume d'une cuve à fonds GRC 29-04-13 à 17:36

Pardon erreur de ma part:
Rt = 0.1*Rcs

Posté par
GaBuZoMeure : Volume d'une cuve à fonds GRC 29-04-13 à 17:41

Donc Rt=0,2*H ?

Qu'as tu essayé ? Qu'est-ce qui te bloque ?

Posté par
LePecre : Volume d'une cuve à fonds GRC 29-04-13 à 18:49

Oui, Rt = 0.1*Rcs = 0.2*H
A vrai dire je ne me suis pas encore lancé dans des calculs. Je pensais utiliser des intégrations en divisant le réservoir en 3 solides distincts:
- le corps cylindrique (dont le volume ne pose pas de problème);
- la calotte sphérique;
- l'élément torrique situé entre ces 2 derniers.
Le fait de ne pas connaitre la position des centres des cercles me parait être un problème pour la détermination des bornes et la résolution de ce calcul. Peut être est il possible de se placer sur le point d'intersection des deux arcs de cercle, à l'endroit de la tangence, pour se servir des équations des 2 arcs de cercle à la fois...?
Les mathématiques n'étant pas mon fort, ce qui me bloque est de savoir comment modéliser mon problème et ainsi débuter sa résolution!

Posté par
GaBuZoMeure : Volume d'une cuve à fonds GRC 29-04-13 à 18:58

Il y a tout de même un centre de cercle dont tu connais la position : celui de rayon Rt.
Il faut un peu de géométrie pour déterminer la position du raccord entre le cercle de rayon Rt et celui de rayon Rcs. Mais avec une bonne figure, en utilisant le fait que le point de raccord et les centres des deux cercles sont alignés (puisque les deux cercles sont tangents au point de raccord), on y arrive sans problème.

Posté par
LePecre : Volume d'une cuve à fonds GRC 02-05-13 à 19:01

Bonjour, désolé je reprends mon problème seulement aujourd'hui.
Oui j'ai bien fais une figure pour définir le point d'intersection entre les deux cercles de rayons Rt et Rcs, un triangle rectangle dont les sommets de son hypoténuse sont les centres de ces mêmes cercles.
Mais pour ce qui est de la démarche à suivre pour trouver le volume total, auriez vous une idée ou conseils que je puisse essayer et vous communiquer mes observations?

Posté par
GaBuZoMeure : Volume d'une cuve à fonds GRC 02-05-13 à 19:18

La technique me paraît simple  : découper en morceaux (calotte sphérique, cylindres, morceau engendré par la révolution d'une part de disque. Pour le volumes de révolution, on peut utiliser Guldin.

Posté par
LePecre : Volume d'une cuve à fonds GRC 06-05-13 à 16:09

Bonjour,
Décidément ca ne me parait pas très simple à moi...

J'essaie de passer par les formules de volumes pour la calotte sphérique notamment. Le problème est que j'ai besoin de la hauteur de la calotte pour déterminer son volume, je ne trouve pas le moyen de la calculer?

De plus, pour le volume de révolution et d'aprés le théorème de Guldin, pour calculer un volume de révolution il faut multiplier sa surface par le cercle que décrit son centre d'inertie autour de l'axe de rotation.
Mais comment définir les dimensions de mon solide de révolution, qui est ici une portion de cercle, pour ensuite définir son centre d'inertie?
Merci par avance.

Posté par
GaBuZoMeure : Volume d'une cuve à fonds GRC 06-05-13 à 16:26

Comme je l'ai déjà dit, la clé de tout ça est la position du raccord entre le cercle de rayon Rt et celui de rayon Rcs. C'est la première chose à laquelle tu dois t'attaquer, et je t'ai indiqué comment.

Posté par
LePecre : Volume d'une cuve à fonds GRC 06-05-13 à 17:29

Autant pour moi merci beaucoup!!
Par construction, en se servant du fait que les centres et le point d'intersection des deux cercles sont alignés, je trouve finalement la hauteur de la calotte sphérique et par conséquent son volume.

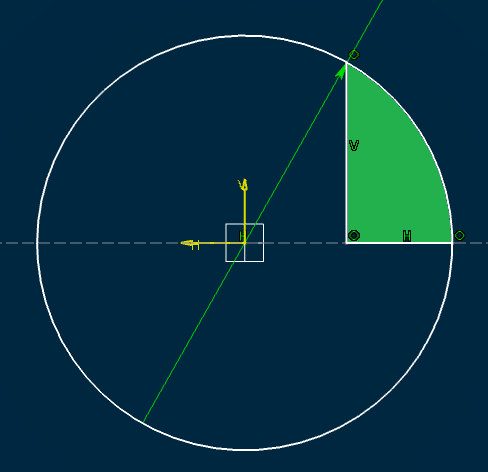
Le reste parait plutôt simple en effet. Il me reste seulement à trouver le centre d'inertie de ma portion de cercle (allure en vert sur la figure ci-joint), seul volume manquant pour compléter ma cuve à fonds GRC.Sachant que le rayon ainsi que les côtés de la section en vert sont connus.

Volume d\'une cuve à fonds GRC

Posté par
delta-Bre : Volume d'une cuve à fonds GRC 07-05-13 à 08:06

Bonjour.

@ LePec

Quand vous parlez 'portion de cercle' c'est plutôt portion de disque qu'il fallait dire.
Le problème pour vous est la mise en forme des intégrales soit pour déterminer le centre d'inertie de cette portion de disque ou pour calculer le volume engendré par rotation de cette portion de disque que je vais noter par D.
1) Coordonnées du centre d'inertie.
  Je vais traiter l'intégrale double \int\int_D f(x,y)dxdy.
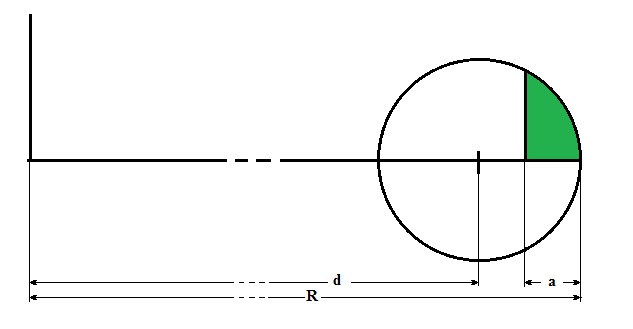
  En prenant comme origine du repère cartésien le centre du disque et en notant par a la longueur du segment horizontal, D peut être défini par

D=\{(x,y) \in \mathbb{R}^2   / R-a\le x \le R, 0 \le y \le \sqrt{R^2-x^2}\}

et on aura

\int\int_D f(x,y)dxdy = \int_{R-a}^R (\int_0^{\sqrt{R^2-x^2}}f(x,y)dy)dx.

2) On peut calculer directement le volume engendré par la portion de disque. La projection de ce volume sur le plan Oxy est une couronne circulaire centrée à l'origine et délimitée par les cercles de rayon R-a et R. En coordonnées cylindriques V peut être défini par

V=\{(r,\thete,z) \in \mathbb{R}^3 / 0 \le \theta \le 2\pi,  R-a \le r \le R,  0\le z \le \sqrt{R^2-r^2}\}

et:

\int\int\int_V dxdydz = \int_0^{2\pi} (\int_{R-a}^R (\int_0^{\sqrt{R^2-r^2}}\,rdz)dr)d\theta=\int_0^{2\pi} (\int_{R-a}^R \sqrt{R^2-r^2}\, rdr)d\theta.

sauf erreur

Posté par
delta-Bre : Volume d'une cuve à fonds GRC 07-05-13 à 08:11

Bonjour.

Corrigez la définition donnée V, une faute de frappe a fait disparaitre un \theta

V=\{(r,\red{\theta},z) \in \mathbb{R}^3 / 0 \le \theta \le 2\pi,  R-a \le r \le R,  0\le z \le \sqrt{R^2-r^2}\}

Posté par
LePecre : Volume d'une cuve à fonds GRC 15-05-13 à 17:10

Bonjour,
Merci pour cette réponse complète et désolé de commenter ton message seulement maintenant.
Pour la méthode de calcul du volume je comprends bien et je suis d'accord.

Ce que je ne vois pas c'est à propos de la détermination du centre d'inertie de la portion de disque.
Dans l'intégrale $\int{\int \limits_{D} {f(x,y)\ dx dy}}$ ; la fonction f(x,y) est l'équation de la portion de disque? Comment la déterminer?
Merci par avance.

Posté par
delta-Bre : Volume d'une cuve à fonds GRC 15-05-13 à 18:54

Bonjour.

Salut LePec

Mon post du 7/5/13 à 8h06 (Extrait)

Citation :
Le problème pour vous est la mise en forme des intégrales soit pour déterminer le centre d'inertie de cette portion de disque ou pour calculer le volume engendré par rotation de cette portion de disque que je vais noter par D
1) Coordonnées du centre d'inertie.
  Je vais traiter l'intégrale double \int\int_D f(x,y)dxdy.
.
Ceci pour faire d'une pierre 3 coups si je peux me permettre l'expression.
Mon but était le calcul d'une intégrable double sur D dans le cas le plus général, f(x,y) est tout simplement la fonction à intégrer, elle n'a aucun lien avec le domaine D.
L'écriture \int\int_D f(x,y)dxdy sous la forme d'intégrales simples répétées :
\int\int_D f(x,y)dxdy = \int_{R-a}R\int_0^{\sqrt{R^2-x^2} fait apparaître les bornes d'intégration qui elles ne dépendent que D.
Pour l'obtention des coordonnées du centre de masse de D, vous aurez à calculer les 3 intégrales doubles (si mes souvenirs sont exactes) \int\int_D dxdy (aire de D), \int\int_D x dxdy  et  tex] \int\int_D y dxdy[/tex]

Posté par
delta-Bre : Volume d'une cuve à fonds GRC 15-05-13 à 18:57

Bonjour

Correction

L'écriture \int\int_D f(x,y)dxdy sous la forme d'intégrales simples répétées :
\int\int_D f(x,y)dxdy = \int_{R-a}^R\int_0^{\sqrt{R^2-x^2} fait apparaître les bornes d'intégration qui elles ne dépendent que D.
Pour l'obtention des coordonnées du centre de masse de D, vous aurez à calculer les 3 intégrales doubles (si mes souvenirs sont exactes) \int\int_D dxdy   aire de D), \int\int_D x dxdy  et   \int\int_D y dxdy

Posté par
LePecre : Volume d'une cuve à fonds GRC 16-05-13 à 17:55

Salut Delta-B,

Oui en effet, l'expression d'une pierre 3 coups était de mise!
Je comprends mieux maintenant; mais comme tu le dis plus haut, pour le calcul volumique de la portion de disque l'obtention du centre d'inertie n'est donc pas obligatoire sauf si on veut utiliser Guldin?

Citation :
2) On peut calculer directement le volume engendré par la portion de disque. La projection de ce volume sur le plan Oxy est une couronne circulaire centrée à l'origine et délimitée par les cercles de rayon R-a et R. En coordonnées cylindriques V peut être défini par

V=\{(r,\thete,z) \in \mathbb{R}^3 / 0 \le \theta \le 2\pi,  R-a \le r \le R,  0\le z \le \sqrt{R^2-r^2}\}

et:

\int\int\int_V dxdydz = \int_0^{2\pi} (\int_{R-a}^R (\int_0^{\sqrt{R^2-r^2}}\,rdz)dr)d\theta=\int_0^{2\pi} (\int_{R-a}^R \sqrt{R^2-r^2}\, rdr)d\theta.

Ayant besoin uniquement du volume, j'utilise cette démarche?

Posté par
delta-Bre : Volume d'une cuve à fonds GRC 16-05-13 à 19:37

Bonjour.

Salut LePec

OUI, la méthode à choisir est laissée à l'utilisateur.
Il est parfois plus utile d'utiliser le théorème de Guldin  cf volume du tore.
Il y a un petit problème au niveau du site, les expressions LaTeX ne sont pas traduites.

Posté par
delta-Bre : Volume d'une cuve à fonds GRC 16-05-13 à 22:00

Bonjour.

Le petit problème a été résolu. Les expressions LaTeX  sont maintenant traduites .

Posté par
star-mathre : Volume d'une cuve à fonds GRC 16-05-13 à 22:11

Citation :
Le petit problème a été résolu. Les expressions LaTeX  sont maintenant traduites .



je pense que le problème de connexion c'est tous

Posté par
delta-Bre : Volume d'une cuve à fonds GRC 17-05-13 à 00:33

Bonjour.

Citation :
je pense que le problème de connexion c'est tous


je pense que le problème de connexion c'est tout

Posté par
star-mathre : Volume d'une cuve à fonds GRC 17-05-13 à 00:37

Citation :
c'est tout

Merci c'est tout

Posté par
LePecre : Volume d'une cuve à fonds GRC 17-05-13 à 18:08

Bonjour à tous,

@ delta-B

Pour en revenir au problème, je comprends bien la triple intégrale pour le calcul du volume, merci encore pour tes indications.
J'ai cependant une question concernant l'application de Guldin ou non : pour un solide de révolution autour d'un axe qui ne coupe pas le solide (type tore). Pour calculer son volume et si l'aire de la surface du solide est déjà connue, est-il possible de passer par un calcul intégral sans connaitre le centre d'inertie?

Posté par
delta-Bre : Volume d'une cuve à fonds GRC 17-05-13 à 19:14

Bonjour.

Salut Lepec

Citation :
Pour calculer son volume et si l'aire de la surface du solide est déjà connue, est-il possible de passer par un calcul intégral sans connaitre le centre d'inertie?


Ce n'est pas la surface du solide qu'il faut connaitre mais l'aire de la surface plane qui lui a donné naissance et la distance entre le centre de masse et l'axe de rotation pour pouvoir appliquer le théorème de Guldin, le plan de la surface devant contenir l'axe de rotation.

Pour calculer le volume V d'un solide D quelconque, sa surface n'est d'aucune utilité pour calculer son volume mais une définition de ce corps.( Problème classique: Quel est, parmi tous les parallélépipèdes  de même volume V, celui qui à la plus petite aire? (c'est le cube de coté \sqrt[3]{V}))

Posté par
LePecre : Volume d'une cuve à fonds GRC 17-05-13 à 23:23


\\ \int\int\int_V dxdydz = \int_0^{2\pi} (\int_{R-a}^R (\int_0^{\sqrt{R^2-r^2}}\,dz)dr)d\theta=\int_0^{2\pi} (\int_{R-a}^R \sqrt{R^2-r^2}\, dr)d\theta.\\ \\ \int_0^{2\pi} (\int_{R-a}^R {R*\sqrt{1- \frac{r^2}{R}}  dr)d\theta  On pose \frac{r}{R} = cos\alpha \\

Posté par
LePecErreur 17-05-13 à 23:28

Pardon pour ca, impossible de supprimer...
Je termine mon message et je le renvoie complet.

Posté par
delta-Bre : Volume d'une cuve à fonds GRC 18-05-13 à 00:34

Bonsoir

Salut LePec

Citation :
\int\int\int_V dxdydz = \int_0^{2\pi} (\int_{R-a}^R (\int_0^{\sqrt{R^2-r^2}}\,dz)dr)d\theta=\int_0^{2\pi} (\int_{R-a}^R \sqrt{R^2-r^2} dr) d\theta

Je vais peut-être vous devancer.
Il manque un 'r' dans \int_0^{2\pi} (\int_{R-a}^R \sqrt{R^2-r^2}dr)d\theta.. Il fallait écrire:
\int_0^{2\pi} (\int_{R-a}^R \sqrt{R^2-r^2}\red{r} dr)d\theta. et le problème du calcul intégral ne se pose plus.

Posté par
LePecre : Volume d'une cuve à fonds GRC 18-05-13 à 00:44

Je viens seulement de voir ton message. Pourquoi ce "r"?
Ci dessous le début de mon calcul par changement de variable pour déterminer le volume du "segment torique".

\\ \int\int\int_V dxdydz = \int_0^{2\pi} (\int_{R-a}^R (\int_0^{\sqrt{R^2-r^2}}\,dz)dr)d\theta=\int_0^{2\pi} (\int_{R-a}^R \sqrt{R^2-r^2}\, dr)d\theta.\\ \\ V = \int_0^{2\pi} (\int_{R-a}^R {R*\sqrt{1- \frac{r^2}{R}}  dr)d\theta  ;  \text{On pose}  \frac{r}{R} = cos\alpha \\ \\ V = -R^2 \int_0^{2\pi} (\int_{r1}^{r2} {\sqrt{1- cos^2{\alpha}} * sin{\alpha}  d\alpha)d\theta  ;  \text{Car}  dr=-R*sin{\alpha}  d\alpha\\ \\ V = -R^2 \int_0^{2\pi} (\int_{r1}^{r2} {sin^2{\alpha}}  d\alpha)d\theta = -R^2 \int_0^{2\pi} (\int_{r1}^{r2} {\frac{1-cos{(2\alpha)}}{2}}  d\alpha)d\theta \\ \\ \text{[...]} \\

Peut être y a t il une autre méthode pour ce calcul dans ce cas? Je ne sais pas comment m'y prendre...

Posté par
delta-Bre : Volume d'une cuve à fonds GRC 18-05-13 à 00:51

vous avez mal recopié l'intégrale que je vous avais donné, vous avez omis le jacobien du changement de variables

Posté par
delta-Bre : Volume d'une cuve à fonds GRC 18-05-13 à 00:59

Votre résultat ne vous semble-t-il pas bizarre, un volume négatif? Que valent les bornes r_1 et r_2

Posté par
delta-Bre : Volume d'une cuve à fonds GRC 18-05-13 à 02:32

Laissez tomber mon dernier message

Citation :
Votre résultat ne vous semble-t-il pas bizarre, un volume négatif? Que valent les bornes r_1 et r_2


L'intégration est correcte car r_1\ge r_2 mais elle ne représente pas le volume ni même la mienne d'ailleurs, Le volume V que j'ai considéré est celui engendré par une rotation autour d'un axe vertical passant par le centre du cercle et non pas autour d'un axe vertical (quelconque). Il faudra refaire les calculs en prenant comme axe des z l'axe de rotation.

Posté par
LePecre : Volume d'une cuve à fonds GRC 20-05-13 à 00:38

Comment s'y prendre pour calculer le volume pour un axe de rotation ne passant pas par le centre du cercle?
Ce ne sont pas seulement les bornes qui changent?
C'est ca que je n'arrive pas à modéliser dans mon problème.

Posté par
delta-Bre : Volume d'une cuve à fonds GRC 20-05-13 à 02:42

Bonjour.

Salut LePec

On va reprendre en prenant l'axe de rotation pour axe des z et utiliser les coordonnées cylindriques x=r \cos\theta, y=r \sin\theta, z=z. le plan Oxy contiendra le centre du cercle générant la partie torique.
On pose d=Rc-Rt,R_1=Rt, R=Rc.  On peut écrire pour le tore engendré par le disque [tex](r-d)^2+z^2=R_1^2
La partie du tore à considérer vérifie z\ge 0 donc z=+\sqrt{R_1^2-(r-d)^2} et < r <R_2

Posté par
delta-Bre : Volume d'une cuve à fonds GRC 20-05-13 à 03:59

Bonjour.

Salut LePec

On va reprendre en prenant l'axe de rotation pour axe des z et utiliser les coordonnées cylindriques x=r \cos \theta, y=r \sin \theta, z=z. le plan Oxy contiendra le centre du cercle générant la partie torique.
On pose d=Rc-Rt,R_1=Rt, R=Rc.  On peut écrire pour le tore engendré par le disque (r-d)^2+z^2\le R_1^2. La partie du tore à considérer vérifie z\ge 0 donc z\le+\sqrt{R_1^2-(r-d)^2} et R-a\le r \le R et \theta \in [0,2\pi].
Le solide S dont on veut calculer le volume est défini en coordonnées cylindriques par S=\{(r,\theta,z), \theta \in [0,2\pi],r \in [R-a,R], 0\le z \le \sqrt{R_1^2-(r-d)^2} . on aura alors pour son volume V:

\\ \int\int\int_V dxdydz = \int_0^{2\pi} (\int_{R-a}^R (\int_0^{\sqrt{R_1^2-(r-d)^2}}\,dz)rdr)d\theta=\int_0^{2\pi} (\int_{R-a}^R \sqrt{R_1^2-(r-d)^2}\, rdr)d\theta.=2\pi\int_{R-a}^R \sqrt{R_1^2-(r-d)^2}\, rdr
L'intégrale \int_{R-a}^R \sqrt{R_1^2-(r-d)^2}\, rdr peut se calculer par changement de variable t=r-d

Sauf erreur dans la définition S

Volume d\'une cuve à fonds GRC


Rechercher
Menu
Espace membre
14 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1741 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !