Inscription / Connexion Nouveau Sujet
Suite de fonctions & convergence uniforme
Bonjour,
Voilà je lisais un cours sur les suites de fonctions (convergence simple, uniforme ..). Et il y a un exemple qui me trouble.
Une suite de fonctions peut converger simplement sans converger uniformément.
Ains la suite définie sur
En effet,
La convergence n'est donc pas uniforme.
Pourtant la convergence est simple, donc

 )
)
En admettant que la convergence ne soit pas uniforme : est-ce dû au fait que
Ainsi il ne peut pas y avoir de discontinuité en 1, et c'est donc pour ça que
Merci de m'éclairer sur ce point

(je crois que je ne vois pas pourquoi convergence simple convergence uniforme )
Reviens à la définition avec les epsilons.
Par analogie c'est un peu comme continuité simple et uniforme, t'as vu ça ?

Salut tout le monde 
Gui_tou >> Voici un bon exemple qui va te faire comprendre en quoi l'implication est bancale:
On prend n€N*.
fn est définie par: 0 si x > = 1/n.
1 si x = n
Sinon, on se débrouille pour que sa courbe forme un triangle isocèle sur [0,1/n].
(Fais un dessin, sinon tu comprendras que dalle).
Il est clair que (fn) tend vers la fonction nulle, mais on voit aussi très bien pourquoi la convergence n'est pas uniforme.

Salut les gars 
Kéké > ok pour Dini, ça confirme un peu ce que je préssentais ^^
J'ai la déf avec les epsilon : en fait j'affine ma question.
Avec la conv simple, on a :
Avec la conv uniforme :
Fixons . Donc d'après la conv simple, quel que soit
, il existe un rang
à partir duquel
.
Donc si on choisit , on a alors
et donc
non ?

(ou bien justement ce n'existe pas toujours .. ?)
Par analogie c'est un peu comme continuité simple et uniforme, t'as vu ça ?
Non ^^
Ayoub > merci pour l'exemple
 On a clairement
On a clairement Pff jsuis nul

salut 
ton sup sur I vaut peut être (et ici, surement) et du coup tu ne peux plus conclure ...
Prend l'exemple suivant
sur
et
sur
Elle tend simplement vers 0 (en écrivant avec les espilons, c'est évident).
Cependant, elle ne tend pas uniformément vers 0, puisque pour tout n,
Salut,
ton n'existe pas toujours effectivement,
il faut comme tu vois que soit majoré dans IN et c'est pas toujours le cas (en plus il faut que ce soit vrai pour tout
.
Salut les gars 
Okk merci. J'avais besoin de cibler le hic, c'est donc l'existence (ou pas) de
Je réfléchis à tout ça et je poste si besoin est.
Merci à tous 
Salut !
On peut visualiser facilement ce que représente cette convergence uniforme.
Si la suite de fonctions converge uniformément vers une fonction
, ca veut dire que pour un
fixé, si l'on trace un "tuyau" (je vois pas d'autre mot) de rayon
autour de la fonction limite, alors a partir d'un certain rang, les graphes des
seront tous dans ce tuyau.
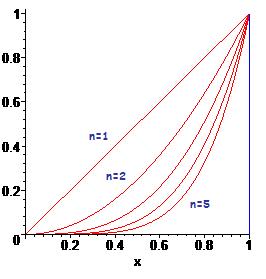
Sur le graphe que tu as posté, on voit que les ne rentrent pas dans un tube centré sur l'axe des abscisses, pour
Ils sortent tous de ce tube, a cause du , et de la continuité.
Si c'est pas clair, hésite pas 

Bonjour gui_tou et tous les autres.
En effet, il y a un théorème qui dit que la limite uniforme d'une suite de fonctions continues est continue. et la suite que tu donnes est un exemple type où l'on conclut que la convergence n'est pas uniforme, puisque la limite n'est pas continue.
Alors je suggère d'étudier toujours sur [0,1] la suite
gn(x)=xn(1-x)
Bonjour Arkhnor et Camélia 
Vi Arkhnor, dans un vieux bouquin j'ai lu cette interprétation graphique ! (à la place de tuyau : enveloppe ?  )
)
Oki Camélia 
La suite (gn) de fonctions converge uniformément vers la fonction nulle sur [0,1], right ?
Merki !
Les fonctions sont continues et positives sur [0,1] et atteignent donc un maximum. De plus f(0)=f(1)=0 et donc ce maximum est atteint sur (0,1).
Il suffit de remarquer que le max est toujours atteint en n/(n+1) et de calculer f_n(n/(n+1)) pour voir que la convergence est uniforme sur [0,1].
a+
Salut Arkhnor,
Pour cette histoire de tube, que doit-on prendre pour epsilon ?
Parce que si je prends epsilon=1, toutes les courbes sont dans ce tube, non ?
MErci !
Bonjour à tous,
Je reprend ce que tu disais un peu plus haut gui-tou
J'ai la déf avec les epsilon : en fait j'affine ma question....Fixons
 >0 ;Donc d'après la conv simple, quel que soit x
>0 ;Donc d'après la conv simple, quel que soit x I, il existe un rang N(
I, il existe un rang N( ,x) à partir duquel lfn(x)-f(x)l
,x) à partir duquel lfn(x)-f(x)l

je suis d'accord. Mais quand tu écris :
Donc si on choisit N0=supx
 IN(
IN( ,x) ...
,x) ...là, je ne suis pas d'accord, car, comme tu le dis toi-même juste en dessous, on ne peut pas garantir que ce sup existe, bref, que cet ensemble d'entiers naturels soit fini puisqu'on prend une infinité de valeurs de x.
Oui voilà Fradel, c'est le hic que j'essayais de saisir, je ne voyais pas ce qui clochait!
C'est la même histoire pour continuité simple/uniforme ?
Merci 



 analyse en post-bac
analyse en post-bac