Inscription / Connexion Nouveau Sujet
Série
Bonsoir .
Un est définie par : Uo>0 et U(n+1)=Un/(1+n.(Un)2) .
1.Montrer que Un est décroissante strictement.
2.En déduire que Un est convergente .
3.a. Vérifier que , pour n
* , fn:x
x/(1+nx2) est croissante sur [0,1/n] .
b.En déduire que 
n* , Un ]0,1/n] .
c.Que peut-on en déduire sur la limite de Un?
4.a. Montrer que , pour n
3, (1/Un)-(1/U(n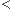-1))
1.
b.En sommant ces inégalités , en déduire que : n2, Un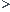
1/(n-2+(1/U2)) .
5.a. Montrer alors que Un
1/n .
b. Conclure quant à la nature de la série (
Un) .
j'ai fais les question 1,2 et 3.a.
3.b. j'ai calculé fn(0) et fn(1/n) et je trouve fn(0)=0 et fn(1/n)=1/(n+1)<1/n . donc fn[0,1/n] et donc U(n+1)]0,1/n] donc Un]0,1/n] mais je ne suis pas du tout sur de cette réponse car on ne sais pas si Un [0,1/n] .
merci d'avance .
Bonsoir,
Pour ton 3b), on le saura au moyen d'un raisonnement par récurrence (vu que ta suite est définie par récurrence !).
Thierry
.Thierrypoma : tu es sur de toi ? car on nous dit en déduire . donc c'est à partir de ce qu'on a fait précédemment et non avec un résonnement par récurrence .
Bonsoir,
Tu as raison ; pas de raisonnement par récurrence en la circonstance. Mais, comment t'y prendrais-tu ?
Thierry
ma première idée a été de dire que sur [0;1/n] fn[0,1/n]
donc U(n+1)]0,1/n] et donc Un]0,1/n] .
mais je pense pas que cela soit bon .
du coup maintenant je sais pas trop .
Attention aux notations...
Résumons : Pour ,
en vertu du ...
Maintenant, que peut-on dire sur ? En effet, ou bien
, ou bien
. La méthode de disjonction des cas permettra alors de conclure.
Errata :
Attention aux notations...
Résumons : Pour ,
en vertu du ...
Maintenant, que peut-on dire sur ? En effet, ou bien
, ou bien
. La méthode de disjonction des cas permettra alors de conclure.
Bonjour
c'est bien une récurrence que tu dois faire, le "en déduire" est là parce que c'est la question précédente qui va te servir à prouver l'hérédité ....
1/n ?Bonsoir,
Je suis d'accord avec Lafol dont l'idée était celle du 25-10-14 à 22:11. Je ne sais pas pourquoi j'ai ensuite dévié vers autre chose... Je suis désolé.
Thierry
Du reste, s'il n'y a que , alors l'énoncé est défaillant... En effet, l'on a
pour
entier quelconque.
thierry, moi aussi, passé une certaine heure, il m'arrive de défaillir 
rien de grave, on est suffisamment nombreux sur l'île pour se remettre dans les rails les uns les autres quand ça nous arrive 
si ça n'est pas dans l'énoncé, non
mais tu prouves que , et tu fais ta récurrence pour n supérieur ou égal à 2 ...
en fait, n est variable, entre 0 et 1/0 n'aurait pas de sens ..
et pour , c'est entre 0 et 1/1 qu'il devrait être, mais comme il vaut
, on n'a aucun moyen de le savoir, donc on commence avec n=2. pense aux identités remarquables pour prouver que
est bien inférieur ou égal à 1/2...
Annuler
connectez vous
analyse en post-bac