Bonjour le denominateur est faux de ta derivee c'est (x+1)² donc il est forcement toujours positif ( c'est un carre)
Et quand au 20 c'est une constante positif donc ça ne changera pas le signe

d'accord avec foxgunner, sauf que le dénominateur de la dérivée est (x² + 1)².
pour le reste c'est bon !

Oups oui le dénominateur est (x+1)²
Mais, quand on parle de signe d'une fonction, on parle du signe de toute la fonction, sur l'intervalle [-infini ; +infini] non ?
Je ne comprends ce qu'on veut dire par "20 ne modifiera pas le signe car il est positif, tout comme le dénominateur qui est au carré"
C'est à dire que je ne vois pas le rapport entre le signe sur l'intervalle et le signe de la fraction
Je sais pas si je suis clair

salut
20 est toujours positif

(x²+1)² est aussi toujours positif donc le signe de ta derivee est celui de -2x²-3x+2

Bonojur ta fonction est definie R-{-1}

Si (-2x² - 3x + 2) est negatif si tu le pultiplie par 20 ça ne change rien ( le produit d'un postif et d'un negatif est nrgatif )


Si (-2x² - 3x + 2) est positif si tu le pultiplie par 20 ça ne change rien ( le produit d'un postif et d'un positif est positif )

    Bonsoir Derko. Si tu étudies le signe d'une fonction, d'une dérivée,... tu tiens compte de tous les facteurs avec laquelle elle est composée.

    Tu peux, mais cela ne sert à rien, mettre dans ton tableau de signes , les coefficients comme 20 ici, ou comme (x² +1) ou (x+a)² . Ces quantités qui sont positives, et qui restent positives, ne changeront pas le signe des autres facteurs.

    Donc, pour la fonction :  y = (40x+30)/(x²+1)  =  10(4x+3)/(X²+1), il te suffira d'étudier le signe de  (4x+3) , et conserver uniquement les résultats trouvés, dans le domaine qui t'es imposé.  D'accord ?    J-L

Je viens de me replonger dans des exercices de 2nd avec les études de signes de diverses fonctions... et j'avais oublié qu'il fallait prendre chaque membre de la fonction et les mettre dans le tableau de signes.

Par contre, dans votre exemple y= 10(4x+3)/(X²+1)
Pourquoi peut on omettre (x²+1) ?
Il peut pourtant être positif ou négatif non ?
x²+1=0
x= -V1  ( - racine de 1)


Ce que j'ai du mal à comprendre, c'est comment savoir que ça ne changera pas le signe à l'avance...
Il faut se représenter le tableau de signe mentalement avant ?

Par exemple, s'il y avait eu F'(x)= -20(-2x² - 3x + 2)/ -(x²+1)
Qu'aurait-on fait ?

Correction :F'(x)= -20(-2x² - 3x + 2)/ -(x²+1)²

Ne pas regarder x²+1=0
x= -V1  ( - racine de 1)

Pardon, j'ai fais une bêtise lol...
J'ai pas réfléchis, oui, c'est toujours positif en effet

Salut Derko,

Tu as fait une erreur : x² + 1 = 0 donne x² = -1 qui n'a pas de solution en 2nde.

Il ne faut pas confondre -1  et -1.

Pourquoi ne comprends tu pas que x² + 1 = 0 ? Connais tu des carres negatifs ?

x² + 1 = 0
x² = -1
Impossible et puis de toute façon, c'est un polynome qui représente une parabole dont le sommet a pour ordonnée 1
Je me suis trompé, j'avais pas réfléchis quand j'ai fais cette erreur...
Mais c'est pas vraiment ça mon problème

PS: je rentre en TES et pour moi, x² = -1 n'a pas de solution non plus
Et racine de -1, c'est impossible (enfin, normalement !!)

    Bonsoir. Pour revenir à la question (aux questions) que tu posais, pour étudier une fonction, et essayer de la dessiner (ou en avoir une idée), on peut bien sûr calculer un certain nombre de points, et les reporter sur un graphe.
    Mais en général, comme l'énoncé ne le demande pas (et que les calculatrices se chargent de les dessiner), on commence à étudier la fonction avec sa dérivée.
    On calcule cette dérivée, et on cherche le signe qu'elle prend, quand x varie dans le domaine de définition, ou le domaine imposé par l'énoncé.Pour avoir commodément ce signe, on essaie de factoriser la dérivée, et on étudie cela dans un tableau . C'est plus clair.
    Mais on n'a pas besoin de s'embarrasser de toute l'expression de la dérivée: on étudie seulement le signe des facteurs qui peuvent changer de signe. Les expressions toujours positives, et les constantes, on peut les laisser "tomber", puisqu'elles ne feront pas changer le signe de tout le reste.  Il s'agit bien, ici, du signe de la fonction dérivée, qui donnera ensuite le sens de variation de la fonction elle-même.    J-L

D'accord merci !
J'ai un polycopié avec pas mal de révision de 1ereES
Et j'ai donc une dérivée qui est la suivante:
F'(x)= -2(x-5)(x-1)/(x-3)²
Je dois en déduire le tableau de variation de F
J'ai fais ce tableau avec paint :



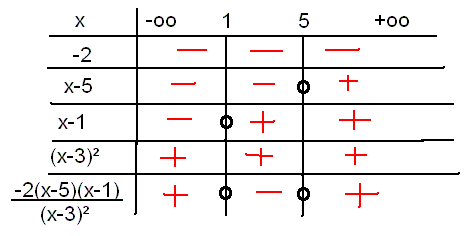
(désolé, je n'utilise pas 'attacher une image' car il y a écrit que c'est pour une figure donc...)

Voilà, je sais pas si j'ai bon mais en tout cas, bien que (x-3)² soit toujours positif, si je ne le mets pas dans le tableau, ça change le signe de la fonction !!
Quelqu'un peut me dire si j'ai bon ? Et si on doit ou pas utiliser (x-3)² !
Merci

édit Océane : image insérée sur le serveur de l'

    Bonsoir Derko. Comme je te l'ai dit l'autre jour, ci-dessus, on n'est pas obligé de mettre les facteurs toujours positifs (du moins sur son brouillon ! ...sur sa copie c'est peut-etre mieux ).

    Tu dis: si je ne mets pas (x-3)², cela change le signe : PAS DU TOUT!
Cela ne change rien, la preuve c'est que dans la ligne de ton tableau, pour (x-3)²  tu n'as que de signes ( + ).

    Tes produits de signes sont faux ! hélas !
Tu aurais pu t'en rendre compte en voyant que pour x très grand (1000, par exemple) on trouve : f'(x) = - 1,9999 . Tu aurais pu le vérifier !

Alors, il faut reprendre cela, pour que tes signes soient conformes au calcul !...   J-L

Oui je me suis trompé
C'est plutôt - sur ]-oo;1] puis + sur [1;5] et enfin - sur [5;+oo[
Et il faut aussi ajouter que lorsque x= 3   , (x-3)² s'annule, ce qui n'est pas possible...
Mais j'ai un gros problème !
En effet, si je remplace x par 1 dans ma fonction de départ qui est (-2x+1) - 8/(x-3) , je trouve 3 .
Ensuite, lorsque x tend vers 3- , la fonction tend vers -oo
Ce qui me donne dans le tableau de signe :
Croissante de [1;3-]... mais pour 1, elle atteind 3 et pour 3-, elle atteind -oo ! Pas du tout logique ?!
Je comprends pas
Qu'est ce qui ne va pas ?

    Comme tu y vas !..." Ce n'est pas logique."... Tu ferais mieux de dire: il y a quelque chose qui m'échappe !...

    En effet, car c'est tout-à-fait logique. La courbe se compose de 2 branches d'allure vaguement parabolique . Tu as compris qu'il y avait une asymptote verticale d'équation : x = 3 . Une des branches, celle de gauche sur le graphe, vient de  + infini ,descend jusqu'au point (1; 3)que tu as trouvé, et remonte à gauche de l'asymptote vers + infini.
    La 2ème branche , à la droite du graphe, monte de - infini le long de l'asymptote, mais à sa droite, atteint le point (5; -13), et redesend vers - infini.
    Pour ne rien te cacher, il y a aussi une asymptote oblique... mais ceci est une autre histoire !...         A plus tard.    J-L

Merci pour l'explication ! Et y a bien quelque chose qui m'échappe puisqu'au préalable, j'ai fait lim f(x) quand x-> 3- (donc à gauche de l'asymptote présente à x= 3 ) et je trouve -oo !!! Et non +oo comme tu me dis.
J'ai peut être fait une erreur de calcul, mais je ce qui n'est pas logique dans mon résultat, c'est qu'elle partirait de y=3 pour croître (car dans le tableau de signe, la dérivée est positive sur cet intervalle) vers -oo ! (c'est ça que je ne trouve pas logique, j'ai dû faire une erreur, mais je ne vois pas !

    Décidément, rien n'est logique avec toi... Cherche , try again !...   J-l