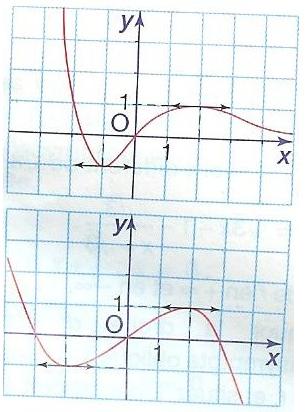Inscription / Connexion Nouveau Sujet
1es les fonctions , les limites
Bonjour a tous j'aimerais avoir de l'aide sur une question d'un exercice :
1) on me demande de " conjecturer " ( ?) graphiquement le domaine de définition de f et les limites de for aux bornes du domaine . Comment faire ??
Je ne sais pas quelle est la différence entre les deux , est ce qu'il faut servir de la formule lim..
J'espère que vous pourrez m'aider sur ce point .
Merci
Eh bien peux tu nous envoyer les graphique pour qu'on puisse te renseigner sur les conhectures de façon fiable???
Pit à Gore
Oui c'est d'accord mais est ce que je peux vous l'envoyer seulement demain ?
Merci de bien vouloir m'aider !
Bonjour amanda5
Pour la première courbe tu t apercois qu'elle elle continue sur R
Aussi on peut conjecturer sur limf(x)=0 quand x tend vers +oo ce qui veut dire que l'axe des abscisses est asymptote à la courbe.
Lorsque x tend vers -oo limf(x)=+oo
Pour la seconde fonction on ne remarque aucune discontinuité sur R
Limg(x)=-oo quand x tend vers +oo et lim g(x)=+oo quand x tend vers -oo
Est ce que tu as d'autres questions Amanda5???
Tu peux me tutoyer au fait!!!
Regarde bien la branche de la première courbe quand x tend vers plus OO elle a tendance à s'approcher et se confondre de l'axe des x donc on peut conjecturer que limf(x)=0 quand x tend vers +oo
OK????
Pour les deux cas Domaine de définition c'esr R
C'est ok!! merci bcp pit a gore pour m'avoir accodé du temps ! je comprend mieux maintenant !! car ça sert a rien de recopier un truc si on ne comprend pas !
j'ai une autre question, qui n'a rien a voir avec les limites , mais par rapport aux courbes de niveaux: sais tu comment on fait les "projections orthogonales" ?
merci encore !
ok. oui c'est la question 4 de cet exercice :
https://www.ilemaths.net/sujet-1ere-es-courbe-de-niveaux-264140.html#msg2269318