Inscription / Connexion Nouveau Sujet
Avec ou sans repère DM de maths
Voici l'énoncé :
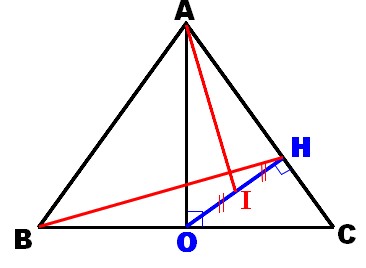
ABC est un triangle isocèle de sommet principal A tel que AB=5 et BC=6. Le milieu O de [BC] se projette orthogonalement en H sur (AC). I est le milieu de [OH].
1. Avec un repère
a) Calculer OA puis justifier que (O ; 1/3 OC , 1/4 OA) est un repère orthonormé. (OA et OC sont des vecteurs)
b) Déterminer dans ce repère les coordonnées d'un vecteur normal à la droite (OH) puis une équation de la droite (OH).
c) Déterminer de même une équation de la droite (AC).
d) En déduire les coordonnées de H puis de AI et BH (vecteurs) ; qu'en déduit-on pour (AI) et (BH) ?
Ceci est la première partie de l'exercice, la deuxième étant "Sans repère". Je la mettrais par la suite. En attendant, j'ai bien réussi la question a) : on trouve OA=4.
Pour la question b), je ne pense pas avoir procéder d'une bonne manière. J'ai dit que le vecteur normal à la droite (OH) est le vecteur CA et ses coordonnées sont (-3;4) L'équation est donc de la forme -3x + 4y + c = 0. Or (OH) passe par A donc -3*0 + 4*0 + c = 0 donc c = O donc l'équation est -3x+4y=0
Je ne suis vraiment pas sur étant donné que pour lka question suivante, quelque chose me parait bizarre en fiasant la même chose. J'attends de l'aide. Merci d'avance.
si vous voulez voir la deuxième partie, c'est :
2. Sans repère
En considérant le triangle AOJ où J est le milieu de [HC], étudier le rôle que joue le point I dans ce triangle et retrouver sans calcul que (AI) et (BH) sont perpendiculaires.
Je réussit vraiment pas, j'attends votre aide. Merci d'avance.
Bonjour,
Juste une petite question de vocabulaire : on te demande les coordonées d'un vecteur normal à (OH). Donc le dit pas "le vecteur normal à (OH)". En effet, si tu prends la droite (OH), tu peux dessiner plein (et même une infinité) de vecteurs normaux à (OH).
Mais je suis d'accord sinon, le vecteur AC est orthogonal au vecteur OH. Donc le vecteur AC est un vecteur normal à (OH).
Regarde bien la droite (OH), elle passe par l'origine du repère, elle est donc de la forme y=kx. Tu trouves quelquechose de ce type là, donc tu ne t'es peut-être pas trompé.
Vérifions cela :
Le point A est de coordonées A(0;4) et le point C de coordonées C(3;0). Le vecteur AC est donc de coordonées AC(3-0;0-4)=AC(3;-4). Tu as pris le vecteur CA qui est donc de coordonées CA(-3;4). Ok sur ce point.
Pour obtenir la droite (OH) tu peux faire de deux manières :
(1) Soit M(x,y) appartenant à la droite (OH). On a alors :
(2) La tienne qui revient au même. Personnellement, je me trompe toujours quand je l'applique donc je préfère appliquer la méthode précédente mais ce n'est qu'une question de goût. Sinon, cela confirme bien ton résultat.
Une petite faute (de frappe je pense) tu dis "Or OH passe par A", je pense que tu voulais dire "passe par O". Sinon, ce ne serait pas juste et pas cohérent avec ce que tu as écrit par la suite.
Ensuite, on cherche l'équation de la droite (AC). C'est un exercice classique d'équation de droite passant par deux points. Tu peux faire avec plusieurs méthodes. Je t'en donne une (qui est du même acabit que la méthode (1)) :
Soit M(x,y) appartenant à la droite (AC). On a alors les vecteurs AM et AC colinéaires.
Le vecteur AM est de coordonées AM(x-0;y-4)=AM(x;y-4). Le vecteur AC est de coordonées AC(3;-4). Donc on a x(-4)-(y-4)(3)=0 c'est-à-dire -4x-3y+12=0 c'est-à-dire y=-4/3x+4.
On vérifie bien que C par exemple, appartient à cette droite :
-4/3*3+4=-4+4=0.
Ensuite, on cherche les coordonées de H (xH,yH). Tu sais que H appartient à (OH) donc yH=3/4 xH. De plus, tu sais que H appartient à (AC) donc yH=-4/3xH+4.
Tu obtiens alors un système que tu devrais savoir résoudre.
Tu pourras alors calculer les coordonées du vecteur BH (en trouvant d'abord les coordonées de B), puis les coordonées du vecteur AI (en trouvant d'abord les coordonées de I). Et tu fais après BH.AI (le produit scalaire) et tu devrais trouver 0. (Il faut faire le produit scalaire car on sent bien qu'ils sont orthogonaux).
Pour la partie sans repère : Montre que I est l'orthocentre du triangle OAJ.
Sauf erreur,
bon courage,
Manuereva
Déjà, merci beaucoup à Manuereva d'avoir pris du temps pour m'expliquer, clairement en plus ! Ca me fait plaisir et je comprend déjà mieux. Mais cependant, quelques petites choses m'échappent :
Je ne comprend pas pourquoi lorsqu'on cherche l'équation de (AC) on prend AM et AC colinéaires alors qu'avant, pour l'équation de (OH), on a pris le produit scalaire OM.AC=O. POurquoi on ne fait pas la meme chose ? Il l'y a pas également un vecteur normal a la droite (AC) ?
Et je ne comprends pas également pourquoi, ayant AM(x;y-4) et AC(3;-4) on multiplie ensuite x(-4) et (y-4)(3). On multiplie le x de AM avec le y de AC ? et le y de AM avec le x de AC ? je ne saisie pas vraiment...
Qu'est-ce que cela donnerait avec ma méthode ? en calculant les coordonnées du vecteur normal et en renplacant dans l'équation, etc. ?
Merci d'avance.
Et aussi, pourquoi met-on un "-" entre les deux multiplications de l'équation de la droite (AC) ?
Désolée de ne répondre que maintenant, j'étaie partie un moment.
Avec le type de méthode que j'emploie, mon truc c'est :
Je prends un point M(x,y) d'une droite (D) dont je cherche l'équation. Je prends un point E connu de cette droite (D) et je cherche alors une relation vectorielle impliquant le vecteur EM et d'autres vecteurs connus : les deux cas les plus fréquents sont :
(1) on connait un autre point de la droite (D) par exemple le point F, dont on connait les coordonées. On peut donc calculer explicitement le vecteur EF. Le fait que M appartient à la droite (D) veut dire que le vecteur EM est colinéaire au vecteur EF.
(2) on connait un vecteur normal à (D), c'est-à-dire que l'on connait les coordonées de ce vecteur. Notons ce vecteur u. Le fait que M appartient à la droite (D) veut dire que les vecteurs EM et u sont orthogonaux.
Voyons à quoi cela correspond si on s'intéresse aux relations vectorielles :
Pour la méthode (1) : Si on a deux vecteurs u(x,y) et v(x',y') colinéaires, cela veut dire que xy'-x'y = 0 (tu as déjà du voir cette relation) d'où le fait qu'il y ait un "-".
Pour la méthode (2) : Si on a deux vecteurs u(x,y) et v(x',y') orthogonaux, cela veut dire que u.v=0 c'est-à-dire que xx'+yy'=0
Pour l'équation de la droite (AC), je suis d'accord, on pourrait chercher un vecteur normal à (AC) ... mais lequel prendre ? le vecteur OH ? Non, justement car on ne connait pas les coordonnées du point H et donc on n'a pas explicitement les coordonées du vecteur OH. Donc voilà, vu qu'on ne connaît pas de vecteur normal explicite (c'est-à-dire dont on connaît les coordonées) à la droite (AC), on ne peut pas appliquer cette méthode.
Si ma méthode pour la droite (AC) te perturbe. Tu peux utiliser la méthode classique : Notons l'équation de la droite (AC) sous la forme y=mx+p (la droite (AC) n'est pas parrallèle à l'axe (OA).
Les points A(0;4) et C(3;0) appartiennent à la droite (AC) donc :
4=m*0+p
0=m*3+p
ssi
4=p
3m=-p
ssi
p=4
m=-4/3
Conclusion : la droite (AC) a pour équation y=-4/3x+4
Je trouve cette démonstration lourde et longue, surtout qu'il y a un système d'équation à chaque fois à résoudre (ca va ici, il est facile à faire vu les coordonées de A et C) et j'avoue que je me trompais toujours dans la résolution de système. D'où ma préférence pour ma méthode avec les vecteurs.
J'espère que je t'ai un peu éclairci ma méthode.


