Inscription / Connexion Nouveau Sujet
Classer des intégrales
Bonjour,
je me permet de créer un nouveau topic puisque l'autre traitait plusieurs questions en même temps. Là ça sera plus clair.
J'ai le même problème que Laetitia
On a :
I(x)= (de 0 à x) ( (tet)/(1+t²)² )dt
(de 0 à x) ( (tet)/(1+t²)² )dt
K(x)= (de 1 à x) ( (et)/(t3) )dt
(de 1 à x) ( (et)/(t3) )dt
L(x)= (de 1 à x) ( (et)/(t4) )dt
(de 1 à x) ( (et)/(t4) )dt
Et pour x 1, nous devons placer I(x), K(x) et L(x) les uns par rapport aux autres.
1, nous devons placer I(x), K(x) et L(x) les uns par rapport aux autres.
Je ne vois vraiment pas comment faire.
Gui-tou nous a fait les courbes (encore merci de nous avoir autant aidé):
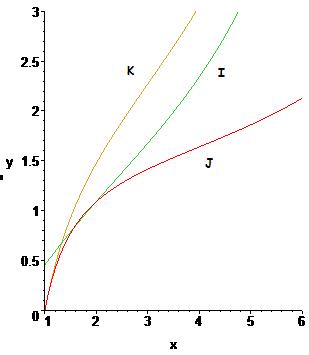
Bon bah en fait c'est bon 
je n'avais pas vu que c'était l'intégrale de 0 à x (et pas de 1 à x) pour I(x)
J'ai
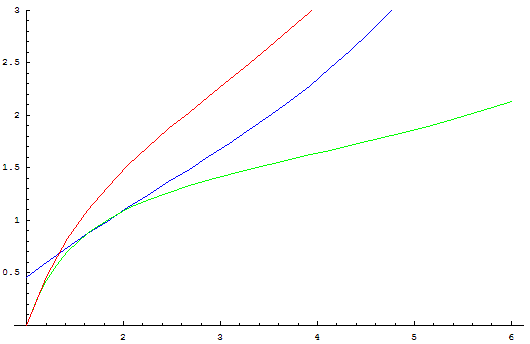
Je regarde ...
Tu es sur de ton I(x), parce que ça me paraît mal parti, si on fait un zoom, on remarque que la courbe de I passe en dessous de celle de J !
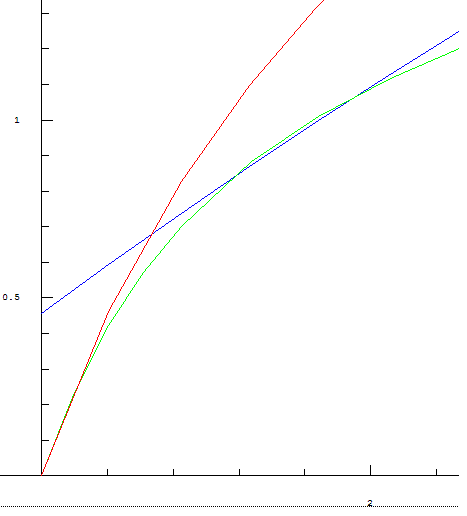
Merci.
Peut être qu'on peut utiliser ma question précédente.
F(x)= f(x) -1 + 2I(x)
avec f(t) = et/(1+t²)
et F(x) =  (de 0 à x) f(t)dt
(de 0 à x) f(t)dt
Parce qu'en fait cette question (ou on doit trouver comment classer les intégrales), c'est une question intermédiaire qui va me permettre de tracer l'allure de la courbe de F(x)
Il n'y a pas de J en fait la fonction c'est L mais ce n'est qu'un détail et ma fonction I est bien celle que j'ai donné.
J'imagines que tu as trouvée cette relation en faisant une intégration par partie :
u'(t) = 2t/(1+t)² et v(t) = exp(t)/2
Je regarde si ça peut aider ...
Pour arriver à ça, poser :
t² = u²+1 dans J(x) et faire une intégration par partie en intégrant 2u/(1+u²)3/2
Et en effet, j'ai bien fait une faute de calcul, le résultat est plutôt :
On peut alors comparer le dernier terme avec I(x) assez facilement.
je pense que l'on tient le bon bout 
I est d'abord entre L (ou J)et K puis inférieure à J et K puis entre J et K puis encore en dessous de J et K.
C'est un peu dur ^^ je ne vois pas comment on peut comparer alors qu'elles n'ont pas les mêmes bornes
Tant pis moi je suis passé aux suivantes. D'ailleurs je bloque (encore!) pour une question.
Avec une intégration par parties soigneusement justifiée, montrez que K(x)-3L(x) est négligeable devant (e^(x))/(x²) lorsque x tend vers + .
.
Je sais que par exemple f est négligeable devant g au voisinage de + si lim (f(x)/g(x))=0 quand x tend vers +
si lim (f(x)/g(x))=0 quand x tend vers + .
.
Est-ce que je dois utiliser ceci? Parce qu'on ne connait pas l'expression des fonctions L et K. Et quelle intégraion par partie puis-je utiliser?
Salut à tous 
Romain, pas fastoche à caser I hein ? 
La fonction
Pour montrer que K(x)-3L(x) est négligeable devant (e^(x))/(x²), je ne sais plus exactement la marche à suivre, mais je sais que c'est long et fastidieux

Je viens (enfin!) de trouver que K(x)-3L(x) = (ex/x3) -e1
Donc ensuite je fais le quotient de mon résultat sur ex/x² quand x tend vers 0
J'ai une forme indéterminée que je n'arrive pas à résoudre.
Je dois donc trouver que la limite de (ex-x3e1)/(xex) a une limite égale à 0 quand x tend vers + .
.
J'ai essayer de transformer la fonction j'obtiens 1/x-x²e-x+1 et là encore FI.
Quelqu'un voit-il comment trouver la limite?
Donc je viens de montrer que L(x) est négligeable devant ex/x² quand x tend vers + .
.
Mais comment je peux trouver que L(x) est négligeable devant ex/x² quand x tend vers + ?
?
Bon ben je pense que mon exercice est un cas désespéré ^^ (et moi également). J'vais arrêter de chercher, j'abandonne ^^
Par contre "MPSI" si tu arrives à avancer un peu n'hésites pas à en parler sur le forum.
Bonne soirée
Je viens de réussir à montrer que L(x) est négligeable devant (ex)/(x²) lorsque x tend vers + .
.
(J'avais également montrer que K(x)-3L(x) est négligeable devant (ex)/(x²) lorsque x tend vers + .)
.)
(F(x)=f(x)-1+2I(x))
Quelqu'un a une idée pour la question suivante:
En déduire un équivalent simple de F(x) lorsque x tend vers +

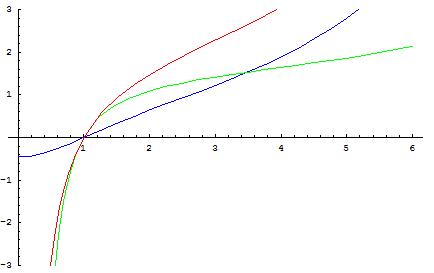



 analyse en post-bac
analyse en post-bac