bonjour

je ne suis pas certain de ce que j'avance

je me sers de (1+x)^a = 1+ax+... où je dis, peut être à tort que le a est lnx (**)

ln(1+x)/x = 1-x/2

donc (1-x/2)^lnx = 1-(x/2).lnx+...

comme le x l'emporte sur le ln, tous les produits x^p.(lnx)^q tendent vers 0

et f(x) tend vers 1

ce qui me fait tilter c'est le (**)

rudy

je ne suis pas sure non plus de ça , je crois que le a
non ? corrige moi si j'ai faux

ben justement, j'en suis pas sûr

si un prof passait par là...

le : est en général faux lorsque dépend de comme c'est le cas par exemple pour _{sauf erreur bien entendu}

merci pour la confirmation

alors comment obtenir cette limite de f(x)=(ln(x+1)/x)^lnx pour x->0+ ?

Bonjour Rudy,

C'est très simple.

.
tend vers 1 quand x tend vers 0 (puisque tend vers 0).
La fonction prolongée a une tangente verticale en 0 car est équivalent à qui tend vers l'infini.

merci jandri

je n'ai pas penser à associer xlnx au DL et je m'obnubilais sur un DL en x=0 pour ln, en vain

merci

bonjour

étonné que la tangente en A(0;1) soit verticale (au vu du tracé de la courbe),



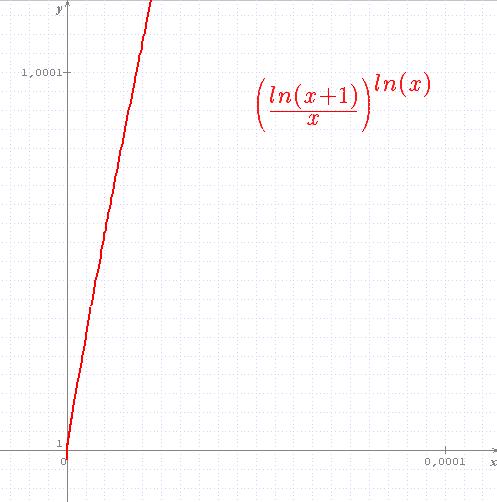
j'ai cherché, par excel, à exprimer delta_y/delta_x pour un pas de plus en plus petit (pas = delta_x)



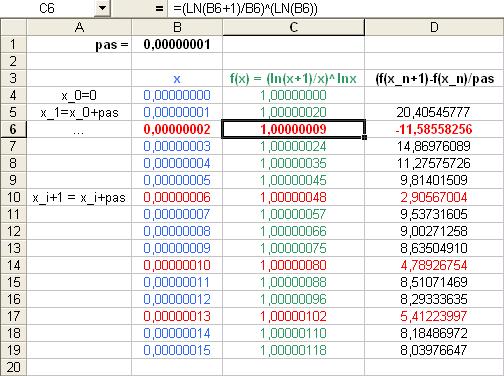
y a-t-il des raisons expliquant les valeurs aberrantes en rouge (le pas n'est que de 0,00000001) ou des moyens d'éviter ces bruits de calcul ?

rudi

Bonjour Rudy,

Ces résultats aberrants sont aisément explicables.
Excel n'est pas une vraie calculatrice.
Il calcule soit-disant avec 15 chiffres significatifs de précision mais ce n'est pas vrai.
Ainsi le calcul de ln(1+2*10^(-8)) donne 2*10^(-8) car il néglige le terme suivant du développement: -4*10^(-16).
Par suite le calcul de ln(1+2*10^(-8)) / (2*10^(-8)) est complètement faux.

Ma calculatrice (TI92) donne pour ln(1+2*10^(-8)) la valeur 1.99999998*10^(-8) qui est correcte.
Elle calcule les bonnes valeurs de f(x) pour x=k*10^(-8) ainsi que les bons taux d'accroissements.
Elle est donc bien supérieure à Excel.

merci jandri

comme je pensais que les 15 chiffres significatifs étaient vrais, je m'étonnais de bugger à 8 chiffres après la virgule

rudy