Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Limites de fonctionsTopics traitant de Limites de fonctions [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Dm Maths

Posté par
magpie 06-11-07 à 11:42

On considère une fonction f dérivable sur R . Sa courbe représentative (C), son asymptote D en -oo et +oo, et sa tangente T en 0 d'équation : y = (1- e) x + 1 sont représentées dans le graphique ci-dessous.

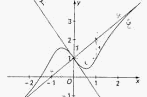
Dm Maths

On suppose en outre que :
- le point J (0 ; 1) est centre de symétrie de (C)
- l'expression algébrique de f (x) est de la forme : f (x) = mx + p + g(x)

où g est une fonction telle que :
lim g(x) en + oo et en - oo = 0

Partie A :
2). Que valent m et p ?
3). Justifier que pour tout x réel, f (-x) + f (x) = 2.
4). En déduire que la fonction g est impaire puis que la fonction f est paire.
5). En admettant que g(x) soit de la forme : g(x) = (ax+b)e^-x² , déterminer alors, à partir de ce qui précède, les réels a et b.

Partie B :
On considère à présent que la courbe (C) représente la fonction f définie sur R par: f (x) = 1 + x - xe^(-x²+1)  1). Calculer f '(X).

2}. Etudier les variations de la fonction f ' sur l'intervalle [0 ; +oo[. Déduire à partir d'un résultat de la partie A les variations de f ' sur ]--oc ; 0]. Dresser ensuite le tableau de variations complet de f '.

3). Montrer que l'équation f '(x) = 0 admet une unique solution w dans l'intervalle [0 ; +oo[, puis que 0, 51 < w < 0, 52.

4). Après avoir exprimé f (w) sous la forme d'un quotient de deux polynômes, établir le tableau de variations de f sur [0 ; +oo[.

Edit Coll : image placée sur le serveur de l' Merci d'en faire autant la prochaine fois ! [lien]    

Posté par
magpieaide 06-11-07 à 11:48

j'ai oublié de vous dire que c'est surtout dans la partie A que je galère. Voilà je vous remercie d'avace pour toute aide

Posté par
magpiere : Dm Maths 06-11-07 à 13:52

help

Posté par
cailloux Correcteurre : Dm Maths 06-11-07 à 14:34

Bonjour,

A)2) La droite d' équation y=x+1 esy asymptote à (C) en -\infty et +\infty

et \lim_{x\to \pm\infty}g(x)=\lim_{x\to \pm\infty}[f(x)-(mx+p)]=0

La droite d' équation y=mx+p est donc cette asymptote et m=p=1

3) J centre de symétrie d' où \forall x\in\mathbb{R},\;\;\frac{1}{2}[f(x_J-x)+f(x_J+x)]=y_J

on en déduit: \forall x\in\mathbb{R},\;\;f(-x)+f(x)=2

4) g(x)=f(x)-x-1

g(-x)=f(-x)+x-1=2-f(x)+x-1=-[f(x)-x-1]=-g(x) et g est impaire.

Ensuite, tu as une erreur dans l' énoncé: il faut démontrer que f' est paire et non pas f:

On dérive les 2 membres de l' expression f(-x)+f(x)=2

soit: -f'(-x)+f'(x)=0 et f'(-x)=f'(x)

f' est donc paire.

5) f(x)=x+1+(ax+b)e^{-x^2}

Comme (C) passe par J(0,1), f(0)=1 d' où 1+b=1 et b=0

D' autre part la tangente à (C) en J(0,1) a pour équation y=(1-e)x+1

donc f'(0)=1-e

f'(x)=1+a(1-2x^2)e^{-x^2} d' où f'(0)=1+a=1-e et a=-e

Finalement l' équation est: f(x)=1+x-ex.e^{-x^2}=1+x-xe^{1-x^2}

Posté par
magpiere : Dm Maths 06-11-07 à 15:10

Merci cailloux mais je comprend pas très bien comment tu fais à la 3).

Posté par
cailloux Correcteurre : Dm Maths 06-11-07 à 15:28

Quelque chose à savoir en Terminale:

Les conditions pour que I(a,b) soit centre de symétrie d' une courbe représentative d' une fonction f:

\{1)\forall x \,\text{\rm tel que}\, a+x\in D_f,\;\;a-x\in D_f\\2)\frac{f(a+x)+f(a-x)}{2}=b

La première condition est ici réalisée puisque f est définie sur \mathbb{R}

Pour cette question 3), j' ai simplement écrit la seconde condition au point J(0,1) centre de symétrie de la courbe.

Posté par
magpiere : Dm Maths 06-11-07 à 19:10

je vais peut-être avoir l'air con mais je vois pas à quoi correspond le signe : A à l'envers ?

je tiens à préciser que quiconque voudrait m'aider pour la partie B serait le bienvenue

Posté par
cailloux Correcteurre : Dm Maths 06-11-07 à 19:27

Re,

\forall x se lit "quel que soit x" ou "pour tout x"

Posté par
cailloux Correcteurre : Dm Maths 06-11-07 à 20:17

B) La fonction donnée est celle trouvée dans le A. Elle a toutes les propriétés vues dans le A et sa courbe est donnée.

1)f(x)=x+1-xe^{1-x^2} définie et dérivable sur \mathbb{R}

f'(x)=1+(2x^2-1)e^{1-x^2}

2) f''(x)=[4x-2x(2x^2-1)]e^{1-x^2}=-2x(2x^2-3)e^{1-x^2}

f''(x)=0 pour x=0 ou x=\sqrt{\frac{3}{2}} sur [0,+\infty[

sur [0,\sqrt{\frac{3}{2}}], f''(x)\geq 0 et f' est strictement croissante.

sur [\sqrt{\frac{3}{2}},+\infty[, f''(x)\leq 0 et f' est strictement décroissante.

On sait que f' est paire, donc:

sur ]-\infty,-\sqrt{\frac{3}{2}}], f' est strictement croissante.

sur [-\sqrt{\frac{3}{2}},0], f' est strictement décroissante.

3)f'(0)=1-e<0 f'(\sqrt{\frac{3}{2}})>0 et \lim_{x\to +\infty}f'(x)=1

sur [\sqrt{\frac{3}{2}},+\infty[, comme f' est continue et strictement décroissante, f'(x)>0

sur [0,\sqrt{\frac{3}{2}}], f' est continue et strictement croissante.

On peut appliquer le corollaire du TVI et il existe \alpha unique, \alpha\in [0,\sqrt{\frac{3}{2}}] tel que f'(\alpha)=0

Par encadrement successifs, on trouve 0.51<\alpha <0.52

4)On en déduit que:

sur [0,\alpha], f'(x)\leq 0 et f est décroissante.

sur [\alpha,+\infty[ f'(x)\geq 0 et f est croissante.

On a f'(\alpha)=0 soit 1+(2\alpha^2-1)e^{1-\alpha^2}=0

d' où e^{1-\alpha^2}=\frac{1}{1-2\alpha^2}

et f(\alpha)=\alpha +1-\alpha e^{1-\alpha^2}=\alpha+1+\frac{\alpha}{2\alpha^2-1}=\frac{2\alpha^3+2\alpha^2-1}{2\alpha^2-1}


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !