Niveau école ingénieur

écriture d'une intégrale sous forme d'une somme finie

Posté par
mouradIII 20-12-09 à 13:53

bonjour,
voici un petit problème que j'ai rencontré. j'ai essayé avec la somme de Riemann mais en vain.
merci d'avance.

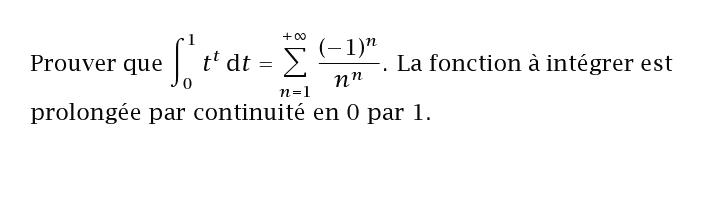
$écriture d\'une intégrale sous forme d\'une somme finie$

Posté par re : écriture d'une intégrale sous forme d'une somme finie 20-12-09 à 13:54

Bonjour,
c'est une somme infinie, non ?
Ca suggère fortement de développer l'intégrande en série.

Posté par écriture d'une intégrale sous forme d'une somme finie 20-12-09 à 14:03

Je ne parviens pas à écrire t^t sous la forme d'une série.

Posté par re : écriture d'une intégrale sous forme d'une somme finie 20-12-09 à 14:27

salut

t^t = exp(t.ln(t))

Posté par écriture d'une intégrale sous forme d'une somme finie 20-12-09 à 14:34

enfin, ça marche. merci beaucoup et bonne journée à tous.

Posté par re : écriture d'une intégrale sous forme d'une somme finie 20-12-09 à 14:34

salut
expo(tlnt) comme une serrie en tlnt et integre

Posté par re : écriture d'une intégrale sous forme d'une somme finie 20-12-09 à 22:34

Bonsoir ;

une petite réctification : $5$\fbox{\int_0^1\;t^t\;dt=\Bigsum_{n=1}^{+\infty}\;\frac{(-1)^{n-1}}{n^n}}$

Posté par re : écriture d'une intégrale sous forme d'une somme finie 21-12-09 à 13:10

Allez faisons les choses proprement !

$\fbox{*}$ Pour $t\in[0,1]$ (fixé) on sait que la série $\Bigsum_{n\ge0}\frac{(t\ell nt)^n}{n!}$ est convergente de somme $e^{t\ell nt}=t^t$

et comme en plus cette série est alternée (assez facile à voir) la majoration du reste donne , pour tout $n\ge1$ , $\left|t^t-\Bigsum_{k=0}^{n-1}\frac{(t\ell nt)^k}{k!}\right|\le\frac{|t\ell nt|^n}{n!}$

une petite étude de $x\to x\ell nx$ sur $[0,1]$ donne $\sup_{0\le x\le1}|x\ell nx|=e^{-1}$

d'où , pour tout $n\ge1$ , $4$\fbox{\left|t^t-\Bigsum_{k=0}^{n-1}\frac{(t\ell nt)^k}{k!}\right|\le\frac{e^{-n}}{n!}}$

$\fbox{*}$ Par intégration sur $[0,1]$ on obtient , pour tout $n\ge1$ , $5$\fbox{\left|\int_0^1\;t^t\;dt\;-\;\Bigsum_{k=0}^{n-1}\;\frac{1}{k!}\;\underb{\fbox{\int_0^1\;t^k\ell n^kt\;dt}}_{a_k}\right|\le\frac{e^{-n}}{n!}}$

$\fbox{*}$ A mon avis il ne doit pas être difficile de montrer que $4$\fbox{\forall k\in\mathbb{N}\;,\;a_k=\frac{(-1)^kk!}{(k+1)^{k+1}}}$

$\fbox{*}$ Et on obtient alors $5$\fbox{\forall n\ge1\;,\;\left|\int_0^1\;t^t\;dt\;-\;\Bigsum_{k=1}^{n}\;\frac{(-1)^{k-1}}{k^k}\right|\le\frac{e^{-n}}{n!}}$ _{sauf erreur bien entendu}

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

analyse en post-bac
21 fiches de mathématiques sur "analyse" en post-bac disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

écriture d'une intégrale sous forme d'une somme finie

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths