Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première FonctionsTopics traitant de fonctions [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

Exercice aire maximale d'un triangle

Posté par
olorin 27-10-09 à 16:58

Bonjour,
Pour après les vacances notre prof de math nous a donné un exercice dont l'énoncé est le suivant :

Citation :
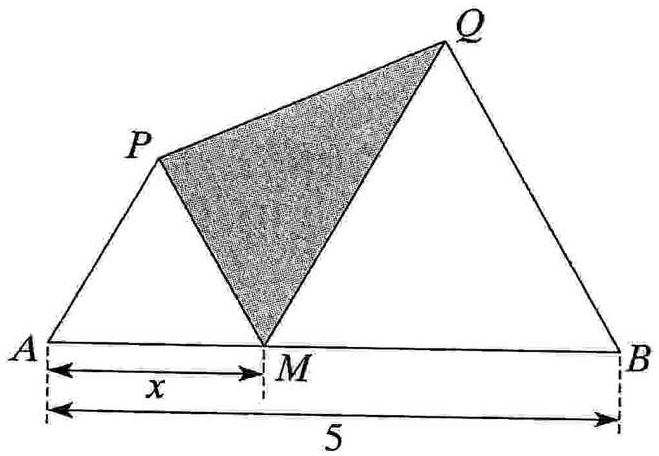
On considère un point M sur [AB]. Les triangles AMP et BMQ sont équilatéraux.
On pose AB=5 et AM=x
1)Déterminer la position de M pour laquelle l'aire de PQM est maximale
2)Déterminer la position de M pour laquelle l'aire du quadrilatère ABQP est minimale.


La figure qui va avec cet exercice est jointe.
J'ai beau chercher je ne vois pas de moyen de calculer l'aire sans avoir les hauteur des triangles.

Merci d'avance pour votre aide.

Exercice aire maximale d\'un triangle

Posté par
Leeloore : Exercice aire maximale d'un triangle 27-10-09 à 17:04

Une piste : MQ=MB=5-x et PM=MA=x

Posté par
abdel01re : Exercice aire maximale d'un triangle 27-10-09 à 17:13

bonjour

le sujet est dejà traité dans ce forum

cliques sur cette page -------> DM maths "aire maximale"

Posté par
freniclere : Exercice aire maximale d'un triangle 27-10-09 à 17:18

Bonjour

Une piste en image. Comme PM est parallèle à QB, QH = MH' :

Exercice aire maximale d\'un triangle

Posté par
olorinre : Exercice aire maximale d'un triangle 27-10-09 à 17:37

Merci je vais suivre sur l'autre topic que je n'avais pas vu ^^

MODERATEUR: Vous pouvez archiver ce topic

Posté par
abdel01re : Exercice aire maximale d'un triangle 27-10-09 à 17:39

ou alors

dans le tiangle PHM rectangle en H:

l angle MPH = 30°

cos(MPH)= PH/x

3/2 = PH/x

6$ PH =\frac{\sqrt{3}}{2}x

d ou aire du triangle MPQ

6$A(x) = \frac{\sqrt{3}}{4}x(5-x)

sauf erreur bien sûr !

Exercice aire maximale d\'un triangle

Posté par
olorinre : Exercice aire maximale d'un triangle 27-10-09 à 18:23

Ta figure n'est pas bonne il faut que H soit sur AM pour que l'angle HPM soit égal à 30° car APM est équilatéral ...

Posté par
abdel01re : Exercice aire maximale d'un triangle 27-10-09 à 18:26

comment ca?

angle PMH = 60°
angle MHP = 90°
angle HPM = ????

Posté par
olorinre : Exercice aire maximale d'un triangle 27-10-09 à 18:35

Je l'avais pas vu comme ça j'étais parti sur l'explication de l'autre topic a ce sujet ^^
Ton expression de l'aire est bonne mais je n'ai pas de polynôme du second degré donc je peux pas savoir la valeur de x pour laquelle l'aire est maximale ...

Posté par
abdel01re : Exercice aire maximale d'un triangle 27-10-09 à 18:53

eh bin! ce n est pas un polynome du second degré?

6$A(x) = \frac{\sqrt{3}}{4}x(5-x) = -\frac{\sqrt{3}}{4}x^2+\frac{5\sqrt{3}}{4}x \\

Maintenant je ne sais pas qu'elle methode que vous utilisez pour determiner le max.
la dérivée ou forme canonique?

As tu suivi les calculs de l autre topic? ca donne la meme chose?

Posté par
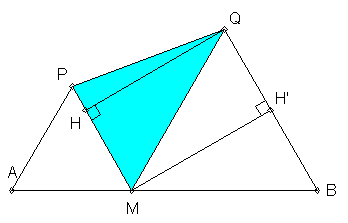
olorinre : Exercice aire maximale d'un triangle 27-10-09 à 20:09

Avec l'autre méthode je trouve ça :

10$\frac{5\sqrt{3}}{4}-\frac{\sqrt{3}*x^2}{8}-\frac{(5-x)^2^\sqrt{3}}{8}


Au fait tu le sors d'ou que:

$10cos(x)=\frac{\sqrt{3}}{2}

Posté par
abdel01re : Exercice aire maximale d'un triangle 27-10-09 à 20:13

cos(30°) = ?????

Posté par
abdel01re : Exercice aire maximale d'un triangle 27-10-09 à 20:17

j ai tout expliquer dans mon post de 17h39

Posté par
abdel01re : Exercice aire maximale d'un triangle 27-10-09 à 20:32

si tu n es pas convaincu, reprenons les calculs avec le dessin posté par frenicle à 17:18

calcul de MH' (pythagore)

6$ MH'^2 + [\frac{(5-x)}{2}]^2 = (5-x)^2

6$ MH'^2 = (5-x)^2-[\frac{(5-x)}{2}]^2

6$ MH'^2 = (5-x)^2-\frac{(5-x)^2}{4}

6$ MH'^2 = \frac{3(5-x)^2}{4}

6$ MH' = \frac{\sqrt{3}}{2}(5-x)=HQ

aire du triangle bleu:

A(x) = (hauteur x base)/2   , ici la base = x

d'ou    
        6$\blue A(x) = \frac{\sqrt{3}}{4}x(5-x)

tu vois quand meme que l autre methode est plus rapide

Posté par
olorinre : Exercice aire maximale d'un triangle 27-10-09 à 20:38

Je veux savoir pourquoi :

10$ cos(MPH)=\frac{\sqrt{3}}{2}

J'ai jamais rien appris qui me dise ca ...

Posté par
abdel01re : Exercice aire maximale d'un triangle 27-10-09 à 20:42

Eh bin desolé mais c'est à savoir!

cos(30°)= cos(/6) = 3/2  non??????????

Posté par
abdel01re : Exercice aire maximale d'un triangle 27-10-09 à 20:43

Vous n avez pas vu la trigonometrie? les angles particuliers à savoir?

Posté par
olorinre : Exercice aire maximale d'un triangle 27-10-09 à 20:44

On voit ça en quelle classe ca ne me dit rien

Posté par
abdel01re : Exercice aire maximale d'un triangle 27-10-09 à 20:49

En premiere mais peut etre vous ne l avez pas encore vu. Si tu regardes sur ton livre le chapitre sur la trigonometrie tu dois avoir un tableau avec differents angles ainsi que leurs sinus et cosinus.

Mais si tu ne l as pas encore vu, tu utilises Pythagore comme je viens de faire dans le post du 20h32 en reprenant la figure posté par frenicle à 17:18, c'est aussi bien et clair!

Posté par
olorinre : Exercice aire maximale d'un triangle 27-10-09 à 21:02

Il n'y a pas un moyen de trouver la même chose sans recourir au point H' parce que même si j'ai compris je m'emmêle avec ton point H et ca me perturbe ...


Je sais je suis chiant

Posté par
abdel01re : Exercice aire maximale d'un triangle 27-10-09 à 21:13

fais un effort

je t'ai fais 2 methodes. Je vais pas en rajouter d'autres plus compliquées! Je ne vois pas en quoi les points H et H' te perturbent !

Posté par
abdel01re : Exercice aire maximale d'un triangle 27-10-09 à 21:16

H c'est le pied de la hauteur de ton triangle. Tu ne peux pas calculer la hauteur QH directement sauf à remarquer qu'elle est egale à MH'

Posté par
olorinre : Exercice aire maximale d'un triangle 27-10-09 à 21:29

Merci de ton aide Abdel01, je vais me débrouiller avec ça ca m'a déjà bien avancé dans mon exercice ^^

Posté par
olorinre : Exercice aire maximale d'un triangle 27-10-09 à 21:36

Pour la question 2) on suit le même raisonement je suppose ?

Posté par
abdel01re : Exercice aire maximale d'un triangle 27-10-09 à 21:45

mais tu n as pas fini deja la premiere !

Pour quelle(s) valeur(s) de x l'aire du triangle est maximale?

je t ai posé la question tout à l heure tu ne m as pas repondu!

comment vous faites en classe pour determiner le maximum d'une fonction, en utilisant la forme canonique ou les dérivées?

je rappelle :     6$\blue A_{PQM}(x) =\frac{\sqrt{3}}{4}x(5-x) = -\frac{\sqrt{3}}{4}x^2+\frac{5\sqrt{3}}{4}x

Posté par
abdel01re : Exercice aire maximale d'un triangle 27-10-09 à 21:47

pour la 2eme, tu calcule les aires des autres triangle et tu fais la somme des 3 aires

Posté par
olorinre : Exercice aire maximale d'un triangle 27-10-09 à 21:51

On utilise la forme canonique, on a pas encore vu les dérivées de fonctions...

Posté par
abdel01re : Exercice aire maximale d'un triangle 27-10-09 à 22:14

donc on a:  

6$\blue A_{PQM}(x) =\frac{\sqrt{3}}{4}x(5-x) = -\frac{\sqrt{3}}{4}x^2+\frac{5\sqrt{3}}{4}x= -\frac{\sqrt{3}}{4}[x^2-5x]

6$ = -\frac{\sqrt{3}}{4}[x^2-5x+(\frac{5}{2})^2-(\frac{5}{2})^2]        j'ai ajouter et retranché (5/2)^2, donc operation neutre, de facon à avoir une identité remarquable

6$ = -\frac{\sqrt{3}}{4}[(x-\frac{5}{2})^2-(\frac{5}{2})^2]

6$ = -\frac{\sqrt{3}}{4}(x-\frac{5}{2})^2+\frac{\sqrt{3}}{4}\times (\frac{5}{2})^2

6$ = -\frac{\sqrt{3}}{4}(x-\frac{5}{2})^2+\frac{25\sqrt{3}}{16}

l aire est donc maximale pour 6$x=\frac{5}{2} et elle (l'aire) est egale à 6$\frac{25\sqrt{3}}{16}

Posté par
olorinre : Exercice aire maximale d'un triangle 28-10-09 à 10:34

Ok Merçi tes calculs sont parfaits, ce sont exactement les bons résulats, j'ai vérifié en faisant varier le point M sur geogebra et je retombe sur tes valeurs ^^

Posté par
abdel01re : Exercice aire maximale d'un triangle 28-10-09 à 11:45

ok tant mieux. Bon courage

Posté par
olorinre : Exercice aire maximale d'un triangle 30-10-09 à 15:21

Abdel01 désolé de te déranger encore mais les droites (PM) et (QB) sont parallèles parce que 10$\widehat{AMP} et \widehat{MBQ} sont égaux (angles alternes-internes) ????

Posté par
abdel01re : Exercice aire maximale d'un triangle 30-10-09 à 15:44

oui c'est ca.

la droite sécante (AB) fait le meme angle avec (PM) et (QB) donc elles sont //

Posté par
olorinre : Exercice aire maximale d'un triangle 30-10-09 à 16:50

Merci j'étais pas sur, j'ai jamais été à l'aise avec les angles alternes internes et tout ça ^^


Dans un autre exercice j'ai quelque chose qui me tracasse j'ai ce système d'équation à résoudre :


5$ x^2+y^2-4=0 \\ y=mx-4m

Je trouve 5$ x^2+m^2x^2-8m^2x+16m^2-4=0 et dans l'exercice on me dit que je dois trouver 5$ x^2+m^2x^2\fbox{+}8m^2x+16m^2-4=0 tu pourrais m'éclairer sur où je me suis planté dans mon développement ?

Posté par
abdel01re : Exercice aire maximale d'un triangle 30-10-09 à 17:04

normalement tu devrais faire un autre topic pour cet exo. Ca facilite la tache aux moderateur pour classer les sujets. Tu veux bien creer un autre en faisant copier coller. Je te rejoins. ok

Posté par
olorinre : Exercice aire maximale d'un triangle 30-10-09 à 17:07

C'est juste sur ce point que je bloque, il faut absolument créer un autre topic ?

Posté par
abdel01re : Exercice aire maximale d'un triangle 30-10-09 à 17:11

je ne vois pas d erreur ds ton developpement.  à moins que ce soit y = mx+4m?

Posté par
olorinre : Exercice aire maximale d'un triangle 30-10-09 à 17:19

C'est l'équation d'une droite passant par un point A(4;0)

y=mx+p
0=4m+p
p=-4m


Je ne vois pas ce qu'il y a de faux la dedans.

Ensuite on demande de trouver les valeurs de x pour lesquelles la droite coupe le cercle C d'équation x²+y²-4=0

Posté par
olorinre : Exercice aire maximale d'un triangle 30-10-09 à 17:20

D'où le petit système d'équation et le développement qui me cause tant de problème.

Posté par
olorinre : Exercice aire maximale d'un triangle 30-10-09 à 17:28

https://www.ilemaths.net/sujet-intersection-de-cercles-et-de-droites-309966.html

J'ai créé un topic parce que je sens qu'on va polémiquer pendant un petit bout de temps ^^


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1674 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !