Qu'on m'arrête si je dis des bêtises, la géométrie n'est pas mon point fort

Si (C) est un tel cercle, alors (C) est circonscrit à MAB et MBC. Donc en particulier, A,B et C sont sur (C). Pour peu que le rectangle ne soit pas plat, alors (C) est nécessairement le cercle circonscrit à ABC, c'est à dire le cercle circonscrit au rectangle.
Puis, par hypothèse M appartient à (C)\{A,B,C} (un cercle circonscrit à 2 points n'a pas de sens) donc au cercle circonscrit au rectangle.

Réciproquement, si on appelle (C) le cercle circonscrit au rectangle, et si M appartient à (C)\{A,B,C}
Alors le cercle circonscrit à MAB est (C) car M, A et B sont dans (C), de même pour MBC

Conclusion : c'est le cercle circonscrit à ABCD privé de {A,B,C}

Je suis surpris par l'interprétation du problème que fait Ulusse.

A mon sens, les cercles circonscits au triangle MAB et les cercles circonscrits au triangle MBC sont

distincts. Ils se coupent en B (fixe) et en M (variable). Les cercles MAB ont leur centre qui se

déplace sur la médiatrice du segment AB et les cercles MBC ont le leur qui se déplace sur la médiatrice du segment BC.

Reste à déterminer le lieu du point M....

Toutefois, il existe effectivement un cas singulier : si l'on choisit comme cercle passant par B et C le cercle circonscrit au rectangle, ce cercle passe aussi par A et B, de sorte que tous les points du cercle sont des points M !

Mais il y a d'autres points. En fait, pour chaque grandeur de cercle choisie (et telle que le diamètre du cercle soit égale ou supérieure à la longueur du rectangle), quatre cercles peuvent être tracés, dont les points d'intersection, outre le point B, sont au nombre de quatre.

Le lieu du point M paraît étrange....

bonjour

pas complètement sûr de ce que j'avance

si ABM est sur un cercle, son centre est sur la médiatrice de AB

si BCM est sur un cercle, son centre est sur la médiatrice de BC

Si c'est le même cercle, son centre est à l'intersection de ces deux médiatrices et donc au centre du rectangle

ce cercle aura R comme rayon R = AC/2

le lieu des points M est donc le cercle de centre I = milieu(A,C) et rayon = AC/2

Sauf erreur

Rudy

Rudy: oui, tu as le même résultat que moi, sauf qu'il faut en priver les points A,B,C sinon on obtient un triangle plat, ce qui n'a pas de sens pour en donner un cercle circonscrit

Priam: honnêtement je ne vois pas de quoi tu parles. Ton raisonnement ne tient pas debout, et "étrange" n'est pas vraiment une conclusion.

J'avais supposé, peut-être à tort, que les cercles ABM et BCM étaient généralement distincts.

L'énoncé est ambigu....

Ulusse

j'y avais pensé avant de poster et, si les triangles sont plats, ce n'est pas grave, le cercle est bien circonscrit aux 2 points AB et BC : je conserverai A, B et C

Rudy

bonjour à tous.

je rectifie:

bonjour esta-fette

pourquoi, au vu de la phrase :

"Déterminer l'ensemble des points M du plan tels que les cercles circonscrits aux triangles MAB et MBC soient égaux"

déduis-tu que les triangles ne peuvent pas être plats ? ou que M , A, B, C ne peuvent pas être alignés ?

si les triangles sont plats, AB et BC sont des cordes du cercle cherché et on retrouve le cercle circonscrit au rectangle

A moins d'avoir mal interprété les données de l'énoncé initial...merci de m'éclairer

Rudy

à Rudy.

Si le cercle circonscrit au triangle MAB existe.

un cercle possède un centre et un rayon FINI.....

donc le centre O du cercle appartient à la médiatrice de MA et à celle de AB.

ces médiatrices sont sécantes. donc non parallèles.
elles sont resp perpendiculaires à MA et MB qui ne sont donc pas parallèles mais sécants...

suis-je clair?

en gros: un triangle aplati ne possède pas UN cercle circonscrit.

d'accord avec cette explication : c'est cette notion d'existence du centre du cercle qui rendait mon analyse erronée

autrement dit, tu confirmes bien ces deux assertions :

- on ne peut concevoir un cercle circonscrit qu'avec, au moins, trois points distincts ?

- tout cercle ayant son centre sur le médiatrice de deux points A et B et passant par ces deux points ne peut pas être qualifié de cercle circonscrit à A et à B ?

Rudy

pour résumer:

un cercle circonscrit à ABC implique

3 points non alignés donc distincts... donc un triangle d'aire non nulle.

Bonjour à tous

Dans les vieux manuels de géométrie, quand on parlait de figures égales, on voulait dire isométriques (cf. par exemple les fameux cas d'égalité des triangles).

A mon avis, c'est comme ça que l'énoncé doit être lu. (C'est aussi la lecture qu'en fait Priam, si j'ai bien compris.)

Autrement dit, les cercles MAB et MBC doivent avoir même rayon. Le cas où ils sont égaux, au sens strict, i.e. identiques, est juste un cas particulier.

Cela dit, je n'ai pas le temps de réfléchir à la question dans l'immédiat.

Cordialement
Frenicle

A première vue, le lieu est la réunion du cercle circonscrit au rectangle et d'une hyperbole.

bonjour Frenicle....


C'est vrai que dans ce sens ça complique énormément le problème.

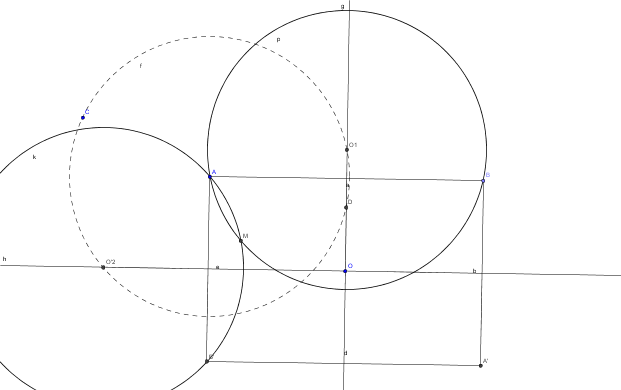
pour construire un point M qui correspond à 2 cercles circonscrits de rayon Rde:

on trace un cercle de centre A et de rayon R, il coupe la médiatrice de BC en O1 et O2
et la médiatrice de AB en O'1 et O'2.

le cercle de centre O1 et de rayon R coupe le cercle de centre O2 et de rayon R en M.

oui, ce serait bien cela: hyperbole + cercle

Bonsoir,

En procédant analytiquement, on trouve effectivement une hyperbole équilatère dont l'axe focal est la médiatrice des petits côtés du rectangle.
Sa distance focale vaut 2(b² - a²), si le rectangle a pour longueur 2b et pour largeur 2a.

Bonjour à tous.

on trouve (analytiquement toujours) dans le plan complexe, on mettant le centre sur le centre du rectangle:
l'hyperbole d'équation:

où est l'affixe du point A.
Cette hyperbole équilatère passe par A; B; C et D, il faut exclure A;B et C

Bonjour,

Pour obtenir simplement l'équation de l'hyperbole, on peut procéder comme suit.
Les notations sont explicitées sur la figure.
S et T sont les centres des cercles respectivement circonscrits à ABM et ACM.

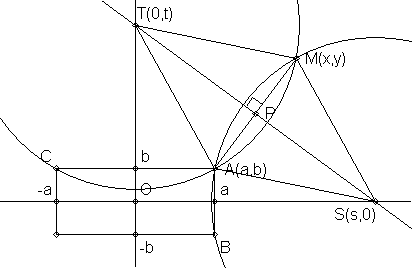
Le quadrilatère ATMS est un losange, donc

1°) Le point P, intersection de ses diagonales, est le milieu de AM et aussi de TS.
Les coordonnées de P sont [((x + a)/2, (y + b)/2] = (s/2, t/2)
D'où, s = x + a et t = y + b.

2°) Les diagonales se coupent à angle droit.
Le produit scalaire AM.TS est donc nul
(x - a).s + (y - b).(-t) = (x - a)(x + a) - (y - b)(y + b) = 0
ou encore
x² - y² = a² - b²

C'est l'équation cherchée.