Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Limites de fonctionsTopics traitant de Limites de fonctions [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

exos de maths,équations,fonction

Posté par
nassmim 23-08-07 à 19:32

besoin d'une correction d'exos pour saoir si j'ai bien fait ou non:

1-resoudre sinx+cosx=2sinxcosx

2-résoudre dans R ce système:
x^3+7x^2y-5y=0
y^3+7xy^2-5x

3-deux cercles tangents en P et Q à une même droite et sécants à M et N
Démontrer que les aires de PMN et QMN sont égales(pas sur de mon raisonnement)

4_trouver toutets les applications bijectives de l'ensemble des entiers nat N dans lui même qui vérifient:pour tout n de N f(n)<(ou égal)n
(rien ompris à celui là lol)

5-E(x)désignant partie réelle de x de R ,càd l'unique entier n tel que
n<(ou égal)x<n+1

montrer que: E[(7n+2)^1/3]=E[(7n+3)^1/3]
j'ai ai passé une demi heure sans trouver

et le dernier que j'ai pas encore commencé:
trouver un ensemble A composé de 10 entiers strictement positifs vérifiant cette propriété:pr tout sous ensemble de A de 6 éléments,la somme de ces six élémens n'est pas divisible par six.
dans la question précédente,peut on remplacer 10 par 11?
voilà si chacun peut m'apporter une correction pour chaque exo c'est hyper cool packe fer un exos sans après savoir si on a réussi ou pas c'est assez énervant!merci àb ientôt

Posté par
mikayaoure : exos de maths,équations,fonction 23-08-07 à 19:46

au fait, bonjour
.

Posté par
mikayaoure : exos de maths,équations,fonction 23-08-07 à 19:48

une façon de faire, parmi d'autres :

1° transforme sinx+cosx en utilisant du pi/4 ( sinx+cosx = V2( (V2/2)sinx + (V2/2)cosx )

2° transforme 2sinxcosx = sin(2x)

A toi...

Posté par
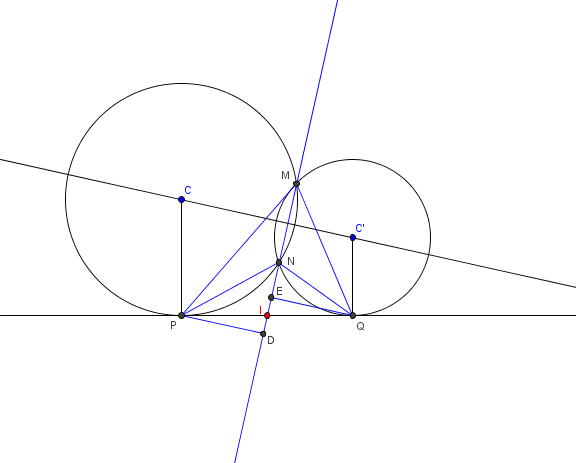
cailloux Correcteurre : exos de maths,équations,fonction 23-08-07 à 22:49

Bonjour,

exos de maths,équations,fonction

3) La droite (MN), axe radical des deux cercles est l' ensemble des points ayant même puissance par rapport à ces cercles.

En particulier, soit I le point d' intersection de (MN) et de la tangente commune (PQ)

IP^2=IQ^2 et IP=IQ

En appelant D et E, les projections sur (MN) des points P et Q:

Les triangles rectangles PID et QEI sont donc isométriques (hypothénuses IP et IQ égales et un angle égal opposé par le sommet)

D' où PD=QE

Ce sont les 2 hauteurs relatives à la base MN des triangles PMN ET QMN: leurs aires sont égales.

Posté par
Dremire : exos de maths,équations,fonction 24-08-07 à 00:13

Pour 4), il n'y a que l'identité comme solution:
par l'absurde, si f(n)\not=n pour un n\in\mathbb{N} alors d'après l'inégalité, en fait f(n)< n. Mais pour tout k< n, l'inégalité donne f(k)\leq k<n. Donc f sur [0,n] ensemble de n+1 éléments ne peut prendre ses valeurs que dans [0,n[ ensemble de n éléments, et par conséquent f n'est pas injective, ce qui est contradictoire avec l'hypothèse f bijective.

On peut aussi démontrer directement par récurrence que \forall n\in\mathbb{N},\ f(n)=n .

Posté par
cailloux Correcteurre : exos de maths,équations,fonction 24-08-07 à 01:08

Bonsoir,

2)En appelant (E) le système de départ, en additionnant et en soutrayant les deux équations:

(E) \Longleftrightarrow \{(x-y)(x^2+y^2+8xy+5)=0\\(x+y)(x^2+y^2+6xy-5)=0

On est donc amené à résoudre 4 systèmes:

A) \{x-y=0\\x+y=0 dont la solution est le couple (0,0).

B) \{x-y=0\\x^2+y^2+6xy-5=0 dont les couples solutions sont \left(\sqrt{\frac{5}{8}},\sqrt{\frac{5}{8}}\right) et \left(-\sqrt{\frac{5}{8}},-\sqrt{\frac{5}{8}}\right)

C) \{x+y=0\\x^2+y^2+8xy+5=0 dont les couples solutions sont \left(\sqrt{\frac{5}{6}},-\sqrt{\frac{5}{6}}\right) et \left(-\sqrt{\frac{5}{6}},\sqrt{\frac{5}{6}}\right)


D) \{x^2+y^2+8xy+5=0\\x^2+y^2+6xy-5=0\} \Longleftrightarrow \{x^2+y^2=35\\xy=-5\} \Longleftrightarrow \{x^2+y^2=35\\4x^2y^2=100\\\rm x et y de signes contraires\} \Longleftrightarrow\{x^2+y^2=35\\(x^2-y^2)^2=1125=15(\sqrt{5})^2\\\rm x et y de signes contraires

Soit 2 systèmes \{x^2+y^2=35\\x^2-y^2=15\sqrt{5}\\\rm x et y de signes contraires\}\;\;\text{ou\:\:\{x^2+y^2=35\\x^2-y^2=-15\sqrt{5}\\\rm x et y de signes contraires\}

Résolvons le premier:

\{x^2=\frac{35+15\sqrt{5}}{2}=\frac{70+30\sqrt{5}}{4}=\left(\frac{3\sqrt{5}+5}{2}\right)^2\\y^2=\left(\frac{3\sqrt{5}-5}{2}\right)^2\\\rm x et y de signes contraires

On obtient les deux couples solutions: \left(\frac{3\sqrt{5}+5}{2};-\frac{3\sqrt{5}-5}{2}\right) et \left(-\frac{3\sqrt{5}+5}{2};\frac{3\sqrt{5}-5}{2}\right)

Puis les deux derniers couples :\left(-\frac{3\sqrt{5}-5}{2};\frac{3\sqrt{5}+5}{2}\right) et \left(\frac{3\sqrt{5}-5}{2};-\frac{3\sqrt{5}+5}{2}\right)

Il y a peut-être une meilleure manière de s' y prendre.

Posté par
Dremire : exos de maths,équations,fonction 24-08-07 à 03:54

Salut cailloux, j'ai un peu plus rapide pour 2): on cherche les solutions autres que (0;0) (la solution A)) sous la forme y=tx,\ x\not=0.
(E)\ \Leftrightarrow\ x^2=\frac{5t}{7t+1}=\frac{5}{t^2(t+7)}\ \Leftrightarrow\ \left(\ x^2=\frac{5t}{7t+1} \text{ et } (t^2-1)(t^2+7t+1)=0\ \right)\ .
Pour t=1, on trouve les solutions B); pour t=-1, solutions C); pour t=\frac{-7+3\sqrt{5}}{2}, solutions D)1; pour t=\frac{-7-3\sqrt{5}}{2}, solutions D)2.

Posté par
Dremire : exos de maths,équations,fonction 24-08-07 à 04:50

5) On veut montrer E(a_n)=E(b_n)  (a_n=(7n+2)^{1/3} \text{ et } b_n=(7n+3)^{1/3}), ce qui est équivalent à: E(b_n)\leq a_n<E(b_n)+1.
Une inégalité est immédiate: a_n<b_n<E(b_n)+1.
D'autre part, E(b_n)\leq a_n\ \Leftrightarrow\ E(b_n)^3\leq a_n^3\ \Leftrightarrow\ E(b_n)^3\leq b_n^3-1\ \Leftrightarrow\ E(b_n)^3<b_n^3\ \Leftrightarrow\ E(b_n)<b_n\ \Leftrightarrow\ b_n \text{ non entier .} Ceci est vrai car si b_n était entier alors b_n^3\equiv 0,1\text{ ou }6 \pmod{7} selon la classe d'équivalence de b_n, ce qui est absurde puisque b_n^3\equiv 3 \pmod{7} .

Posté par
cailloux Correcteurre : exos de maths,équations,fonction 24-08-07 à 11:57

Bonjour,

>> Dremi: Pour le système, je préfére ta solution, plus rapide... et plus homogène

>> nassmim: ils sortent d' où tes exercices ?

Posté par
Dremire : exos de maths,équations,fonction 24-08-07 à 15:22

6) a) Je prends 5 nombres congrus à 0 modulo 6 (par exemple 6, 12, 18, 24 et 30) et 5 nombres congrus à 1 modulo 6 (par exemple 7, 13, 19, 25 et 31). Alors pour un sous-ensemble de 6 nombres parmi ces 10 nombres, si n note le nombre de nombres congrus à 1 modulo 6 parmi ces 6 nombres, 1\leq n\leq 5 et d'autre part la somme des 6 nombres S_n\equiv (6-n)*0+n*1\equiv n \pmod{6} . On en déduit que Sn n'est jamais divisible par 6.

Posté par
infophilere : exos de maths,équations,fonction 24-08-07 à 15:23

Bonjour

Sont sympas ces exos !

Posté par
Dremire : exos de maths,équations,fonction 24-08-07 à 16:20

C'est vrai infophile.

Posté par
cailloux Correcteurre : exos de maths,équations,fonction 24-08-07 à 17:04

Bonjour,

Un début de solution pour le 1)

En élevant au carré:

sin\,x+cos\,x=2\,sin\,x.cos\,x\Longrightarrow 1+sin\,2x=sin^22x

d' où: sin\,2x=\frac{1-\sqrt{5}}{2}=sin\,\phi avec \phi\in]-\frac{\pi}{2},0[

et \{x=\frac{\phi}{2}+k\pi\\\text{ou}\\x=\frac{\pi}{2}-\frac{\phi}{2}+k\pi k\in\mathbb{Z}

Reste à déterminer quelles solutions conviennent...

Posté par
Dremire : exos de maths,équations,fonction 24-08-07 à 18:53

cailloux, ce n'est pas facile de voir les solutions qui conviennent pour conclure avec ta méthode.
On n'a pas besoin d'élever au carré et on garde des équivalences:
2\sin{x}\cos{x}=(\sin{x}+\cos{x})^2-1.
Donc l'équation est équivalente à:
S(x)=\sin{x}+\cos{x}=\sqrt{2}\sin(x+\pi/4) solution de l'équation du second degré S(x)^2-S(x)-1=0.
Les solutions sont donc
\arcsin\left(\frac{1\pm \sqrt{5}}{2\sqrt{2}}\right)-\frac{\pi}{4}+2\pi k;\ \frac{3\pi}{4}-\arcsin\left(\frac{1\pm \sqrt{5}}{2\sqrt{2}}\right)+2\pi k.

Posté par
infophilere : exos de maths,équations,fonction 24-08-07 à 18:57

Très astucieux Dremi

Posté par
infophilere : exos de maths,équations,fonction 24-08-07 à 19:04

Ah je n'avais pas vu la réponse de cailloux du même tonneau

Posté par
cailloux Correcteurre : exos de maths,équations,fonction 24-08-07 à 19:24

Oui Kévin, c' est ce qui fait toute la différence entre un Dremi et des gens comme moi...

Posté par
infophilere : exos de maths,équations,fonction 24-08-07 à 19:54

Il n'y a pas que les maths dans la vie, et tu es déjà très bon (sans parler du \LaTeX )

Non je ne fayote pas

Bonne soirée !

Posté par
Dremire : exos de maths,équations,fonction 25-08-07 à 15:39

6)b) La réponse est non, mais je n'arrive pas à le démontrer sans une aide informatique pour faire quelques dizaines de milliers de calcul à ma place (j'arrive à réduire leur nombre à quelques centaines, mais bon cela reste fastidieux). Si un arithméticien pouvait se pencher sur la question...
On peut écrire le problème d'une façon finie ainsi:
Existe-t-il un 6-uplet (n_0,n_1,n_2,n_3,n_4,n_5) (n_k représente le nombre de nombres congrus à k modulo 6) tel que
11=n_0+n_1+n_2+n_3+n_4+n_5 (on peut se limiter à \forall k,\,n_k\leq5) et
pour tout 6-uplet (m_0,m_1,m_2,m_3,m_4,m_5) vérifiant \forall k,\,m_k\leq n_k et 6=m_0+m_1+m_2+m_3+m_4+m_5,
S=m_1+2m_2+3m_3+4m_4+5m_5\ \not\equiv\,0\,\pmod{6} ?

Posté par
nassmimre : exos de maths,équations,fonction 28-08-07 à 18:06

c'est un exo que j'ai récupéré sur internet je crois!il y a marqué en haut de la feuille entrée en classe prépa à louis le grand mais quand même je trouve ça assez dur,j'ai l'impression qu'il y a des notions que je ne connais pas et que j'urais dusavoir en termninale?ou alr c'est à moi de faire des recherches!
enfin pour le premier exo je vais voir ta méthode mikayaou moi j'avais fait
(cosx + sinx)^2=[sin(2x)]^2
1+2cosxsinx=sin^2(2x)
1+sin2x-sin^2x=0 et après je sais pas comment faire j'ai limpress° kil mank un rien

pour le 2 ac les systèmes,j'avais esasyé de factoriser par (x-y) mais après avoir fait la soustraction des deux systèmes et jme suis embrouillé,et le reste perso j'ai vraiment du mal à comprendre!seul la démonstration sur les aires des trianqles que j'ai comprise mais je crois pas que j'aurais pu trouver seul!
en tt cas merci beaucoup pour votre aide et svp vous etes pas des élèves sortant dfe terminale comme moi j'espère??lol

Posté par
infophilere : exos de maths,équations,fonction 28-08-07 à 18:24

Oui ce n'est pas évident mais ça vient de LLG faut pas s'étonner

Posté par
nassmimre : exos de maths,équations,fonction 28-08-07 à 18:26

un élève qui entre en prépa en llg devrait résoudre ces exos????parce que j'ai dans ma classe des élèves y allant je pense pas qu'ils pourraient tous les réussir

Posté par
infophilere : exos de maths,équations,fonction 28-08-07 à 18:31

Oui je me rappelle avoir fait un test d'entrée (premier DS) de LLG et c'était ce type d'exercice

Tu as un lien ? Car je suis arrivé après la bataille

Posté par
nassmimre : exos de maths,équations,fonction 28-08-07 à 18:35

un lien pour ces exos?non aucun packe jlai pris ya qqes temps sur un autre ordi donc jme rapelle plus quel site et ya donc pas l'historique désolé!par contre je crois...que c'était sur le site louis le grand directment mais pas sur!

Posté par
infophilere : exos de maths,équations,fonction 28-08-07 à 18:36

Ok


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !