Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

fonction bijective

Posté par
ferenc 25-12-11 à 18:42

bonjour,
je n'arrive pas à prouver que la fonction f:\R\to \R^*,x\mapsto x+\sqrt{x^2+1} n'est pas bijective. (mais elle l'est bien sur \R^*_+)

Je résous donc f(x)=y et j'arrive à x=\frac{y^2-1}{2y}
Ainsi, pour moi, x existe et est unique \forall y\in\R^*
merci

Posté par
sabagare : fonction bijective 25-12-11 à 19:01

la fonction considérer est bijective sur \[\left] {0; + \infty } \right[\]

Posté par
sabagare : fonction bijective 25-12-11 à 19:05

\[\begin{array}{c} \\ y = x + \sqrt {{x^2} + 1}  \Rightarrow y - x = \sqrt {{x^2} + 1} \\ \\ \Rightarrow {\left( {y - x} \right)^2} = {x^2} + 1\\ \\ \Rightarrow {y^2} - 2xy + {x^2} = {x^2} + 1\\ \\ \Rightarrow {y^2} - 2xy - 1 = 0\\ \\ \Rightarrow x = \frac{{{y^2} - 1}}{{2y}};\\ \\ y =  - 2 \Rightarrow x =  - \frac{3}{4}\\ \\ x =  - \frac{3}{4} \Rightarrow y =  - \frac{3}{4} + \frac{5}{2} = \frac{7}{4} \\ \end{array}\]

Posté par
sabagare : fonction bijective 25-12-11 à 19:06

\[\left\{ \begin{array}{c} \\ y =  - 2 \Rightarrow x =  - \frac{3}{4}\\ \\ x =  - \frac{3}{4} \Rightarrow y =  - \frac{3}{4} + \frac{5}{2} = \frac{7}{4} \\ \end{array} \right.;\left( {-2\ne\frac{7}{4}}\right)\]

Posté par
atilapre : fonction bijective 25-12-11 à 22:14

bonjour sabaga tu as montré la fonction n'été pas bijective sur \R\backslash\{0,-2\}, mais cela ne démontre pas qu'elle l'est sur \R^+_*

Posté par
sabagare : fonction bijective 25-12-11 à 22:50

bonjour atilap

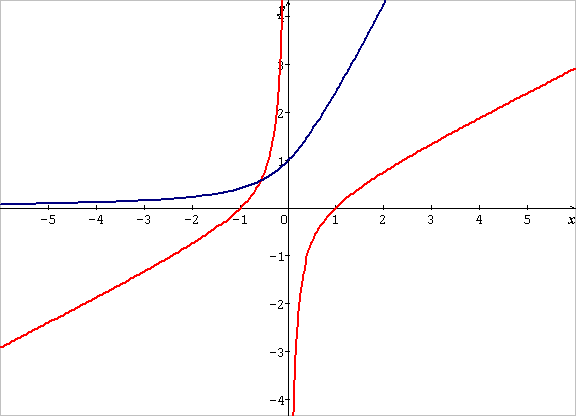
regarder bien on à \[\forall x \in \mathbb{R}:f(x) = x + \sqrt {{x^2} + 1}  > 0\] graphe du fonction f(couleur noir)
c'est-à-dire \[y > 0\]
graphe du fonction g;   \[g\left( y \right) = \frac{{{y^2} - 1}}{{2y}}\]  (couleur rouge)
fonction bijective

* Tom_Pascal > image externe BMP d'un mégaoctet (sympa !!!) récupérée, convertie en gif, puis placée sur le serveur de l', merci d'en faire autant la prochaine fois ferenc ! *

Posté par
jonwamre : fonction bijective 25-12-11 à 23:17

salut,

il suffit de dire que ta fonction est positive (et que comme elle arrive dans R* et pas dans R+* dans ton ennoncé elle n'est pas bijective)

Posté par
ferencre : fonction bijective 26-12-11 à 01:11

ok, j'ai compris, en effet sur le graphe c'est évident !!
Mais lors d'un devoir, j'ai pas le droit à la calculatrice alors comment avoir l'intuition, car dans mes calculs, je ne vois aucune erreur !!
merci,

Posté par
alainpaulre : fonction bijective 26-12-11 à 10:26

Bonjour,


Bien repérer ces fonctions!!

f(x) vérifie
(f(x)+1/f(x))/2=x ,

ou f(x) est l'inverse de  \frac{x+1/x}{2}



Alain

Posté par
ferencre : fonction bijective 26-12-11 à 10:36

pouvez vous développer ? Je suis désolé d'insister mais:
x+\sqrt{x^2+1}=y\Leftrightarrow \sqrt{x^2+1}=y-x \Leftrightarrow x^2 +1 =(y-x)^2\Leftrightarrow x=\frac{y^2-1}{2y}
ainsi, d'après mes calculs on a que x existe pour tout y\neq 0, donc f est surjective sur \R^* et donc bijective sur \R^*. Mais pourtant elle n'est pas bijective sur \R^* donc j'ai forcément fait une erreur, mais je ne vois pas où !!
merci

Posté par
alainpaulre : fonction bijective 26-12-11 à 11:29

Oui,

Tu peux montrer que :
y=x+\sqrt{x^2+1} =>  1/y = x-\sqrt{x^2+1}

d'où ...



Alain

Posté par
ferencre : fonction bijective 26-12-11 à 11:32

en effet, mais ça ne m'explique pas pourquoi mon calcul est faux ^^

Posté par
jonwamre : fonction bijective 27-12-11 à 13:30

bonjour,

je dirais que ta deuxième équivalence est fausse (de droite à gauche il faudrait une valeur absolue) mais je sais pas si c'est ce que tu voulais ... ^^

Posté par
ferencre : fonction bijective 27-12-11 à 14:02

en effet, très bien, cela signifie que on a la condition y\geq x sinon l'équation n'est pas définie sur \R merci beaucoup !!


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !