Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Fonction LogarithmeTopics traitant de Fonction Logarithme [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

fonction LN Bis

Posté par
Nelcar 19-01-21 à 21:34

Bonsoir,
voici la deuxième partie d'un exercice :
Soit f la fonction définie sur ]0 ; + infini[ par f(x)=(2-1/x)((ln(x)-1)+2
On appelle Cf la courbe représentative de la fonction f dans un repère orthogonal.
1) déterminer les limites de la fonction f aux bornes de son ensemble de définition
2) en déduire l'existence d'éventuelles asymptotes à la courbe représentative de f
3) montrer que f'(x)= u(x)/x²  (dans la première partie il était noté u(x)=ln(x)+2x-2
4) en déduire le tableau de variations de la fonction f sur ]0 ; + infini[

voici ce que j'ai fait :
1)x tend vers 0
lim 2-1/x= - infini               lim lnx=- infini par produit f(x)= - l'infini
x tend vers plus l'infini
lim 2-1/x=2                          lim lnx=+ infini  par produit f(x)=+ l'infini
2) il existe une asymptote verticale
3) alors là je n'ai pas trouver pareil donc je ne fais pas la question suivante pour l'instant
j'ai fait uv donc u'v+uv'
u=1-1/x       u'=1/x²  (j'ai mis + car comme j'avais un moins devant -et - = +)
v=2-lnx        v'=-1/x

1/x²*(2-lnx)+(1-1/x)*(-1/x)
je trouve
2-lnx+x+1 le tout sur x²   je ne trouve pas la même chose merci de vérifier

MERCI

Posté par
heklare : fonction LN Bis 19-01-21 à 22:00

f(x)=\left (2-\dfrac{1}{x}\right)\left(\ln x-1\right)+2

f'(x)=\dfrac{1}{x^2}(\ln x -1)+\dfrac{1}{x}\left(2-\dfrac{1}{x}\right)

f'(x)= \dfrac{\ln x-1}{x^2}+\dfrac{2}{x}-\dfrac{1}{x^2} poursuivez on a bien le résultat attendu

D'où sort le 2-\ln x ?

et pourquoi ne pas avoir continuer sur l'autre ?

Posté par
Nelcarre : fonction LN Bis 19-01-21 à 22:30

Re,
oui en effet je me suis trompée dans mes calculs
donc on a bien f'(x)= lnx-1+2x-1 le tout /x²  ce qui donne bien ln(x)+2x-2/x²

ok merci de me dire si ce qui a été fait avant est bon
2) je corrige l'asymptote est horizontale il me semble

et 4) en déduire le tableau de variations de la fonction f sur ]0;+ infini[
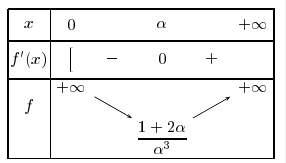
x  0                                             1                                  + infini

f'(x)                   -                       0              +

f(x)    flèche descendante   f ()  flèche remontante

MERCI

Posté par
heklare : fonction LN Bis 19-01-21 à 22:42

N'oubliez pas les parenthèses


On a bien en 0 et en +\infty   comme limites +\infty

L'asymptote est l'axe des ordonnées même raison que pour u

f'(x)=\dfrac{u(x)}{x^2}  La dérivée ne s'annule évidemment pas pour 1

à quoi a servi la partie A ?


Pourquoi un « e »  à trompée  ?

Posté par
Nelcarre : fonction LN Bis 19-01-21 à 23:17

Bonsoir,
je reprendrai cet exercice demain
le "e" je suis du sexe féminin.

Bonne soirée je vais me coucher.

A demain

Posté par
heklare : fonction LN Bis 19-01-21 à 23:32

  Sur votre profil c'est écrit garçon  c'est le pourquoi de la question sinon peu m'en chaut

D'accord  à demain

Posté par
Nelcarre : fonction LN Bis 20-01-21 à 09:25

Bonjour à tous,
hekla : oui c'est vrai au début j'avais mis que j'étais un garçon, un peu la honte  pour moi donc.... et je ne sais pas le changer.

je reviens à l'exercice :
* ok pour la parenthèse
* tu mets pour les limites : On a bien en 0 et en +   comme limites +
moi j'avais mis :
x tend vers 0
lim 2-1/x= - infini               lim lnx=- infini par produit f(x)= - l'infini

x tend vers plus l'infini
lim 2-1/x=2                          lim lnx=+ infini  par produit f(x)=+ l'infini

donc pour x tend vers 0 c'est faux ?  (0*-infini)

2) pour l'asymptote sur ma calculatrice elle était plutôt horizontale, c'est bien quand elle se rapproche de 0 (j'ai vraiment du mal avec ça)

3) c'est bon
4)
en déduire le tableau de variations de la fonction f sur ]0;+ infini[
x  0                                                                               + infini

f'(x)                   -                       0              +

f(x)    flèche descendante   f ()  flèche remontante

MERCI

Posté par
heklare : fonction LN Bis 20-01-21 à 10:56

Si vous voulez changer cliquez sur votre pseudo dans espace membre
puis sur mon profil  et informations personnelles.  Le plus important pour nous est le niveau d'études. Revenons donc à nos moutons

Comme les réponses étaient correctes  je n'ai pas détaillé  et je n'avais mis que les résultats

En détaillant

\displaystyle \lim_{x\to 0}\left(2-\dfrac{1}{x}\right)=-(-\infty)=+\infty \quad \lim_{x\to 0}\ln x -1=-\infty  $donc \lim_{x\to 0}f(x)=-\infty\times -\infty =+\infty \\

\displaystyle \lim_{x\to +\infty}\left(2-\dfrac{1}{x}\right)=2 \quad \lim_{x\to \infty}\ln x -1=+\infty  $donc \lim_{x\to +\infty}f(x)=2\times +\infty =+\infty

2) l'asymptote est l'axe des ordonnées car la fonction n'est pas définie en 0 et \displaystyle \lim_{x\to0}f(x)=+\infty

3 Dérivée  f'(x)=\dfrac{u(x)}{x^2}

4 Il y a bien sûr une double barre en dessous de 0 mais le logiciel que j'utilise ne permet pas  (ou je n'ai pas trouvé de mettre les deux dans la même case)

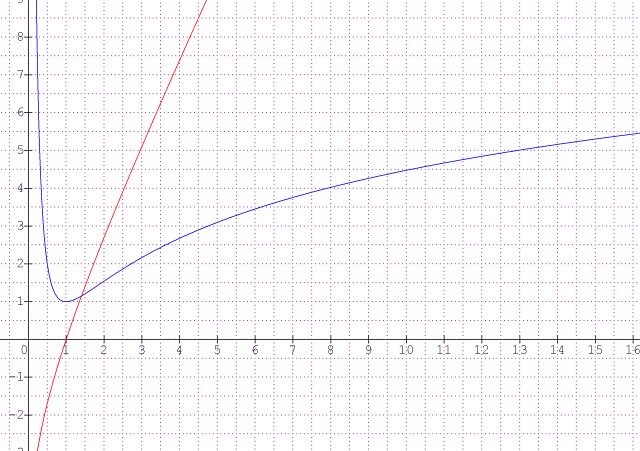
fonction LN Bis

Posté par
heklare : fonction LN Bis 20-01-21 à 11:13

Les courbes  de u (en rouge) et de f  (en bleu)

Comment avez-vous trouvé \alpha \approx 3,8

alors qu'il est manifeste que \alpha=1  en effet \ln 1+2\times 1-2=0

et comme cette valeur est unique !

L'asymptote n'est pas « horizontale »

fonction LN Bis

Posté par
Nelcarre : fonction LN Bis 20-01-21 à 14:51

Re,
je reprends la première question sur les limites
petite question quel est la dérivée de 1/x pour x tend vers 0 et x tend vers + l'infini
c'est bien - infini et + infini

comment fais-tu pour
en 0 :
lim (2-1/x) = -(-infini)
et en + infini
lim (2-1/x)= + infini
c'est pour mieux comprendre

MERCI

Posté par
Nelcarre : fonction LN Bis 20-01-21 à 14:54

Re,
dans ton message de 10 h 56
pour 0
tu as + et - = +
je pense qu'il y a une erreur quelque part
j'essaie de comprendre

MERCI

Posté par
heklare : fonction LN Bis 20-01-21 à 15:17

Les limites de la fonction inverse sont à connaître car c'est sur elles que l'on s'appuie en général

\displaystyle \lim_{x\to 0}\left(2-\dfrac{1}{x}\right)=-(+\infty)=-\infty

en effet   \displaystyle \lim_{\stackrel{x\to 0}{x>0}}\dfrac{1}{x}=+\infty

\lim_{x\to 0}\ln x -1=-\infty  $ donc$ \lim_{x\to 0}f(x)=-\infty\times -\infty =+\infty


la réponse finale était correcte mais il y avait un - en trop  pour la première limite


en + \infty

\displaystyle \lim_{x\to +\infty}\left(2-\dfrac{1}{x}\right)=2  $car $ \lim_{x\to +\infty }\dfrac{1}{x}=0

d'où  en reprenant  la fonction
\displaystyle \lim_{x\to +\infty}\left(2-\dfrac{1}{x}\right)=2 \quad \lim_{x\to \infty}\ln x -1=+\infty  $donc \lim_{x\to +\infty}f(x)=2\times +\infty =+\infty


  

Posté par
Nelcarre : fonction LN Bis 20-01-21 à 15:32

Re,
ok je vais apprendre par coeur la lim de 1/x

la question 2)
on a bien une asymptote verticale
f(x) n'est pas définie dans 0 et la limite quand f(x) tend vers 0 est + l'infini

je commence à comprendre, c'est un peu plus clair dans ma tête

MERCI

Posté par
heklare : fonction LN Bis 20-01-21 à 15:40

Gardez plutôt en mémoire sa courbe
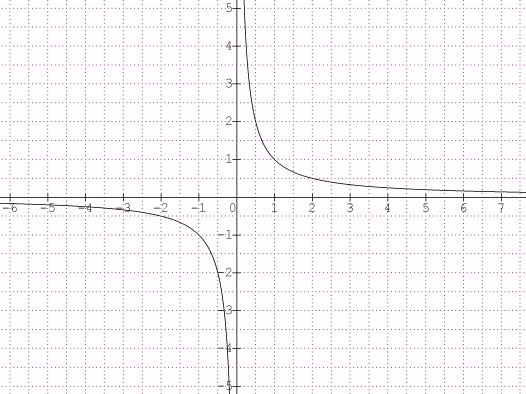
fonction LN Bis

On  retrouve bien qu'en l'infini la limite est 0 et en 0 la limite est \infty

ensuite cela dépend de l'endroit où l'on se trouve

Posté par
Nelcarre : fonction LN Bis 20-01-21 à 15:54

re,
moi j'ai comme sur ton message de 11 h 13 ?
tu as représenté quoi comme fonction là ?

MERCI

Posté par
heklare : fonction LN Bis 20-01-21 à 15:59

la courbe de 11:13 est bien celle de la fonction que vous êtes en train d'étudier



Celle de 15 :40 est la courbe de la fonction inverse et je vous disais que plutôt d'appendre les
limites par cœur   il était préférable d'avoir en mémoire la courbe puisque l'on récupère
facilement les limites

Posté par
Nelcarre : fonction LN Bis 20-01-21 à 16:48

Re,
c'est à dire (car ça m'intéresse pour ne pas apprendre par coeur)
et je ne comprends pas ce que vous notez à savoir :
On  retrouve bien qu'en l'infini la limite est 0 et en 0 la limite est

merci si vous avez des exemples

MERCI

Posté par
heklare : fonction LN Bis 20-01-21 à 17:06

En regardant les branches de cette hyperbole, vous pouvez constater que plus on se déplace vers la droite  plus la courbe a tendance à se rapprocher de l'axe des abscisses   on a donc

\displaystyle \lim_{x\to +\infty}\dfrac{1}{x}=0

et plus on se déplace vers la gauche  plus la branche va se rapprocher de l'axe des abscisses

\displaystyle \lim_{x\to -\infty}\dfrac{1}{x}=0

Quand on s'approche de 0 en étant positif  plus la branche monte

\displaystyle \lim_{\stackrel{x\to 0}{x>0}}\dfrac{1}{x}=+ \infty


On peut aussi penser que plus il y a de monde moins la part du gâteau sera petite  d'où tend vers 0

plus vous découpez une feuille de papier en petits morceaux  plus vous aurez de confettis  donc tend vers \infty

Posté par
Nelcarre : fonction LN Bis 20-01-21 à 17:44

Re,
donc si
lim 1/x    = - infini
xtend vers o
x<0

MERCI

Posté par
heklare : fonction LN Bis 20-01-21 à 17:54

Oui  on peut aussi penser que la fonction est impaire et sa courbe symétrique par rapport à l'origine. Des arguments pour retrouver facilement les limites de cette fonction aux bornes de son ensemble de définition

Posté par
Nelcarre : fonction LN Bis 20-01-21 à 17:57

Re,
merci beaucoup
je vais rechercher des exemples sur internet pour voir si j'ai compris

Encore un grand MERCI pour votre aide

Posté par
heklare : fonction LN Bis 20-01-21 à 18:19

De rien  

Si vous avez besoin d'aide  vous connaissez le site

Posté par
Nelcarre : fonction LN Bis 21-01-21 à 07:48

Bonjour

Oui merci hekla

Bonne journée
et un GRAND MERCI

Posté par
heklare : fonction LN Bis 21-01-21 à 09:51

C'est peu de choses

Bonne journée

Posté par
Nelcarre : fonction LN Bis 21-01-21 à 11:00

Re,
c'est peut-petre peu de choses pour toi mais pour moi c'est beaucoup

MERCI


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !