Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Limites de fonctionsTopics traitant de Limites de fonctions [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

fonctions à deux variables

Posté par
marinouu 29-09-07 à 12:39

bonjour!
j'ai un petit soucis avec une question d'un exercice sur les fonctions.. J'espère que vous allez pouvoir me débloquer!

f(x) = x+ (2)/x + ²

est un réel et >0

on m'a demandé d'étudier les limites de la fonction en + infini.
J'ai trouvé:

lim f(x)= 1 (je ne détaille pas le calcul)

mais là je bloque sur une question ou on me demande de démontrer qu'il existe une asymptote oblique d à la courbe et étudier leurs positions relatives.
Pouvez vous m'aider pour cette question?

merci d'avance
marine

Posté par
raymond Correcteurfonctions à deux variables 29-09-07 à 12:46

Bonjour.

Ton énoncé manque de parenthèses.

A-t-on :

3$\textrm f_{\alpha}(x) = x + \fra{2\alpha}{x} + \alpha^2

ou :

3$\textrm f_{\alpha}(x) = x + \fra{2\alpha}{x+\alpha^2}

ou ... ?

Dans mes deux cas, la limite de 3$\textrm f_{\alpha}(x) en l'infini n'est pas 1.

A plus RR

Posté par
marinouure : fonctions à deux variables 29-09-07 à 12:52

je suis désolée je me suis trompée dans l'énoncé...

f(x) = x+ (2)/x + (²)/(x^3)

voilà, la c'est la bonne fonction

alors d'après la limite des termes de plus haut degrès, j'ai trouvé 1

merci pour votre aide
marine

Posté par
raymond Correcteurre : fonctions à deux variables 29-09-07 à 13:03

Ton expression est composée de trois termes. Lorsque x tend vers l'infini, les deux derniers tendent vers 0. Donc il reste le premier terme x qui tend vers l'infini.

A plus RR.

Posté par
marinouure : fonctions à deux variables 29-09-07 à 13:15

oui je suis d'accord mais pourquoi lorsqu'on met l'expression sur le même dénominateur (x^3) et qu'on utilise la limite des termes de plus haut degrès, on trouve 1 ?

mercii!
marine

Posté par
raymond Correcteurre : fonctions à deux variables 29-09-07 à 13:36

C'est dommage de réduire au même dnominateur, la fonction s'étudie mieux sous sa forme initiale. Cependant, si tu veux réduire quand même, tu trouveras :

3$\textrm f_{\alpha}(x) = \fra{x^4 + \alpha x^3 + \alpha^2}{x^3}

Et tu retrouves la conclusion que je t'ai donnée.

A plus RR.

Posté par
marinouure : fonctions à deux variables 29-09-07 à 13:47

A oui, la limite est bien + infini.
c'est vrai qu'il était plus pratique d'utiliser la première expression!

mais pour ma première question, comment démontrer qu'il existe une asymptote oblique d à la courbe et étudier leurs positions relatives.


merci encore!
marine

Posté par
raymond Correcteurre : fonctions à deux variables 29-09-07 à 15:29

Regarde ton énoncé :

2$\textrm f_{\alpha}(x) = x + \fra{2\alpha}{x} + \fra{\alpha^2}{x^3} = x + \phi(x) \ \ avec lim_{x\to{\infty}}\phi(x) = 0

Donc, l'asymptote est y = x.

Pour la position, étudie le signe de 2$\textrm f_{\alpha}(x) - x c'est-à-dire le signe de 2$\textrm \phi(x) = \fra{2\alpha x^2 + \alpha^2}{x^3}


A plus RR.

Posté par
marinouure : fonctions à deux variables 29-09-07 à 15:55

à ok, je n'y avais pas pensé!
j'ai l'habitude de rencontrer des asymptotes obliques de la forme ax+b
j'étudie le signe et je vous fais part de mon résultat

merci beaucoup (encore et encore!)
marine

Posté par
marinouure : fonctions à deux variables 29-09-07 à 16:31

pour étudier le signe je n'ai pas besoin ed la dérivée ? car j'ai fais sans! il me semble bien que c'est seulement pour les variations, enfin je crois!

Posté par
raymond Correcteurre : fonctions à deux variables 29-09-07 à 16:42

Pour la position, tu n'as pas besoin de la dérivée.

Par contre, tu sais que, par l'énoncé, 2$\textrm\alpha > 0, ce qui facilite bien les choses. En effet, avec les notations de mon précédent topic,

2$\textrm\phi(x) = \fra{2\alpha x^2+\alpha^2}{x^3}

Le numérateur s'écrit : 2$\textrm\2alpha(x^2+\alpha) strictement positif.

Donc, le signe de 2$\textrm\phi (x) est celui de x3, donc de x.

Je t'envoie une image de deux cas : 2$\textrm\alpha = 1/2 et 2$\textrm\alpha = 1

A plus RR

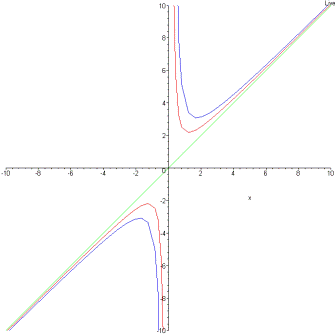
fonctions à deux variables

Posté par
marinouure : fonctions à deux variables 29-09-07 à 17:24

je suis contente car c'est ce que j'avais fait! donc sur mon intervalle I= ]0, + infini[ l'asymptote y=x est au dessus de la courbe (car j'ai trouvé un signe positif sur ]0, + infini[).

par contre ensuite on me demande de calculer la dérivée de la fonction, voilà la dérivée que j'ai trouvé:

f'(x)= [2(x^3) - 3x²(²) + 2]/ (x^5)

ensuite pour étudier son signe j'ai d'abord étudier le signe du trinome [2(x^3) - 3x²(²) + 2] et pour cela je l'ai factorisé.
Ensuite (après plusieurs calculs) j'ai dressé le tableau de signe et je trouve que la fonction est croissante de ]0,(3/2)) puis décroissante jusqu'à (2 /3) puis croissante jusqu'en + infini.

pensez vous que ces résultats sont cohérents?
merci

marine

Posté par
raymond Correcteurre : fonctions à deux variables 29-09-07 à 19:31

Avant toute chose, tu peux remarquer que la fonction est impaire.

Le numérateur de ta dérivée est :

2$\textrm N = x^4 - 2\alpha x^2 - 3\alpha^2

En posant x² = X on arrive à :

2$\textrm N = X^2 - 2\alpha X - 3\alpha^2 : trinôme du second degré.

Je cherche le discriminant et les racines et je trouve :

2$\textrm X' = 3\alpha \ et \ X'' = -\alpha

Cela signifie que l'on peut factoriser :

2$\textrm N = (x^2 + \alpha)(x^2 - 3\alpha)

Le premier terme est > 0, donc le signe de la dérivée est le signe de 2$\textrm x^2 - 3\alpha

trinôme du second degré de racines :

2$\textrm x' = -\sqrt{3\alpha} \ et \ x'' = \sqrt{3\alpha}

La dérivée sera donc négative entre x' et x", positive à l'extérieur de [x', x"].

Remarque : il faudra que tu calcules 2$\textrm f_{\alpha}(\sqrt{3\alpha}) = \fra{16}{9}\sqrt{3\alpha}

Sauf erreurs de calcul.

A plus RR.

Posté par
marinouure : fonctions à deux variables 29-09-07 à 20:02


Je suis trop triste! pff j'ai fait une erreure de calcul en mettant sur le meme dénominateur, et du coup j'ai eu un x^3 au lieu d'un x^4...

merci beaucoup de m'aider!

mais juste au tout début quand je calcul la dérivée j'ai:



f(x) = [x^4 + 2(x²) + ²]/ x^3

et pour calculer la dérivée j'utilise (u'v-uv')/v²

et a la fin il me reste un x^6, je ne comprends pas pourquoi...

merci
marine

Posté par
marinouure : fonctions à deux variables 29-09-07 à 20:08

a j'ai compris je mets en facteur x²!

c'est bien ça ?

oui oui je crois bien!

Posté par
marinouure : fonctions à deux variables 29-09-07 à 20:17

une dernière chose je n'ai pas le meme numérateur que vous...
moi je trouve f'(x) = (x^4)+2x²+2x -3²

alors je ne comprends pas..
je suis perdue

Posté par
raymond Correcteurre : fonctions à deux variables 29-09-07 à 20:38

Dérive avec l'énoncé, c'est bien plus simple :

3$\textrm f_{\alpha}(x) = x + \fra{2\alpha}{x} + \fra{\alpha^2}{x^3}

3$\textrm\Longrightarrow \ f_{\alpha}^^{'}(x) = 1 - \fra{2\alpha}{x^2} - \fra{3\alpha^2}{x^4} = \fra{x^4-2\alpha x^2-3\alpha^2}{x^4}

Ne te décourage surtout pas !!

A plus RR.

Posté par
marinouure : fonctions à deux variables 29-09-07 à 21:36

là je suis d'acord, mais pourquoi lorsqu'on met sur le meme dénominateur je ne trouve pas cela?
bon je vais le faire avec cette expression alors!

merci

Posté par
marinouure : fonctions à deux variables 29-09-07 à 21:40

vous avez raison! je suis vraiment désolée, je suis trop étourdie..
mais il est beaucoup plus simple de prendre l'expression de départ! je ne sais pas pourquoi je veux toujours me compliquer!

mercii beaucoup

marine

Posté par
raymond Correcteurre : fonctions à deux variables 29-09-07 à 21:48

Le calcul d'une dérivée au moyen de (u/v)' demande toujours des calculs assez pénibles. Donc, quand on peut l'éviter c'est mieux.

Heureux d'avoir pu te venir en aide.

A plus RR.

Posté par
marinouure : fonctions à deux variables 29-09-07 à 23:20

petit problème! hé oui encore!

pour f((3)) je trouve: (16)/ (3(3))

et pourtant j'ai bien fait attention...

peut on dire que x= (3) est le minimum de f sur I ]0, + infini[ ?

merci encore
marine

Posté par
marinouure : fonctions à deux variables 02-10-07 à 19:24

alors ?

merci :d
marine

Posté par
luluuuure : fonctions à deux variables 05-10-07 à 22:35

salut! j'aile meme exercice à faire que toi et pour ta dernière question je pense que c'est juste. Par contre comment démontrer que l'emsemble des points P est inclus dans la droite d'équation y= 16/9 x?
voilà, car là je bloque
merci beaucoup à tous, julie


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !