Inscription / Connexion Nouveau Sujet
Joute n°17 : Le tournoi de l’hexagone
Bonjour à tous,
Aujourd'hui, c'est la Saint Arnaud et le comte de Montmirail organise un grand tournoi en l'honneur de son meilleur ami, le baron Arnaud de Brassempouy.
Dans l'une des épreuves, le baron Arnaud et les chevaliers Conrad et Eudes, munis de leur arbalète, se placent après tirage au sort sur les sommets notés A, C et E d'un hexagone régulier.
Ils ne disposent que d'une seule flèche (et ne sont pas censés se tirer dessus  ).
).
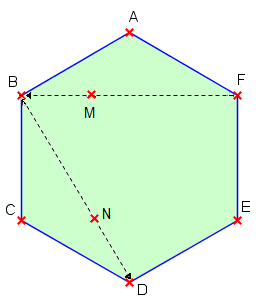
Un pigeon M est lâché du sommet F et vole en ligne droite et à vitesse constante vers le sommet B. Au même instant, un autre pigeon N est lâché du sommet B et vole en ligne droite et à vitesse constante vers le sommet D (à la même vitesse que M).
On aura donc la relation FM/FB = BN/BD = x
On suppose également que les pigeons et les flèches se déplacent dans le même plan horizontal.

Le vainqueur est celui qui réussira le premier à toucher les deux pigeons d'une seule flèche d'arbalète. On suppose que la vitesse des flèches est très supérieure à celle des pigeons.
Questions : qui va remporter l'épreuve et quelle proportion de leur trajet les pigeons auront-ils parcouru ?
Donnez la valeur de x exacte ou arrondie à la 3ème décimale.
 Bonjour
Bonjour
Je dirais que c'est Conrad qui sera le premier dans l'alignement des deux pigeons
et que ce sera le cas lorsque x=1-( 3)/3
3)/3 0,423
0,423
MM
 C'est le chevalier Conrad qui gagnera ... x sera alors égal à 0,42265, soit 0,423 (valeur approchée par excès)
C'est le chevalier Conrad qui gagnera ... x sera alors égal à 0,42265, soit 0,423 (valeur approchée par excès)
 Bonjour,
Bonjour,
Sauf erreur, c'est le chevalier Conrad qui remportera l'épreuve.
La proportion de trajet sera x = 1 -  3/3 ~ 0,423.
3/3 ~ 0,423.
Merci pour cette joute festive  .
.
 Bonjour godefroy_lehardi,
Bonjour godefroy_lehardi,
Le chevalier Conrad va remporter l'épreuve. Proportion du trajet parcouru par les pigeons: 0,423.
Merci pour le tournoi, heu... la joute ! 
 Bonjour Godefroy,
Bonjour Godefroy,
En supposant qu'il sait tirer, c'est (Conrad) qui pourra le premier toucher les deux pigeons d'une seule flèche ; et si la vitesse de cette flèche est infinie, ce sera pour
(mais qu'allait faire Eudes dans cette galère ?)
 Bonjour,
Bonjour,
Il faut donc trouver un alignement entre les points M, N et la position de chacun des tireurs (resp. A, C et E). Quelques observations:
- On suppose la vitesse des projectiles >> que celle des pigeons, on fait donc l'hypothèse que cette vitesse est infinie.
- Notons tout d'abord qu'il ne sera pas possible à Eudes de toucher les deux pigeons avec un unique carreau d'arbalète. En effet, jamais les points N, M et E ne seront alignés: de sa position, Eudes peut soit couper la trajectoire FB, soit couper la trajectoire BD, mais jamais les deux.
- Notons ensuite que Arnaud ne se trouvera aligné avec N et M qu'après que les pigeons aient parcouru au moins la moitié du parcours (en effet, M doit parcourir au moins la moitié de FB avant de "couvrir" la trajectoire de N).
- Notons enfin que Conrad ne pourra voir cet alignement que au cours de la première moitié du parcours. En effet, dans la seconde moitié, le pigeon N ne "couvre" plus la trajectoire FB.
Le vainqueur sera donc forcément Conrad. Reste à trouver quand.
La proportion du trajet parcouru par les pigeons M et N lorsqu'ils seront transpercés par le carreau de Conrad sera donc inférieure à 1/2. Après quelques calculs, on trouve qu'elle est exactement de , soit 0.423 après arrondi.
 Bonjour,
Bonjour,
Je dirais et C remporte l'épreuve.
(Ca paraît toutefois faible comme valeur  )
)
Merci pour l'énigme );
 Bonjour,
Bonjour,
Nous voyons de suite que Eudes n'a aucune chance.
Arnaud ne verra un alignement qu'après Conrad
D'après ma figure géométrique les pigeons issus de
B et de F auront parcouru 0.4226 de leur parcours.
 Bonsoir
Bonsoir
C'est le chevalier Conrad ( celui qui est en C) qui tirera le premier
et x = (3 -  3) / 3 = 0.422
3) / 3 = 0.422
A+
 bonjour,
bonjour,
Si l'on considère que les côtés de cet hexagone font tous 6 cm, alors quand le tireur placé en A tirera lorsque le pigeon M sera a 4/6eme de sa distance, alors le pigeon N sera lui aussi a 4/6eme de sa distance, or d'apres un dessin, la flèche tirée par A touchera les 2 pigeons( si l'on considère que la flèche a bien une trajectoire rectiligne et qu'elle soit tirée avant que les pigeons atteignes les 4/6eme de leurs distances).
conclusion: le tireur A remportera l'épreuve.
les pigeons seront au 4/6eme de leur distance
x sera= 10/6 ou 1.667
 Bonjour/Bonsoir,
Bonjour/Bonsoir,
D'abord qui gagnera ?
- Eudes est disqualifié d'office car il n'aura jamais les deux pigeons alignés dans sa visée.
- Arnaud ne pourra avoir la visée sur le pigeon N que sur la gauche de la ligne AD, et, donc, la visée simultannée que quand M aura parcouru plus de la moitié de son chemin (x > 1/2)
- De même, Conrad ne pourra avoir la visée sur le pigeon M que au dessus (à l'ouest) de la ligne CF, et, donc, la visée simultannée que tant que N n'aura pas encore parcouru la moitié de son chemin (x < 1/2)
Ce sera donc Conrad qui aura la visée simultannée en premier et gagnera.
Ensuite, où sera le pigeon M quand il tirera ?
Pour avoir une visée simultannée, les angles BCM et BCN doivent être égaux (et bien sûr, BN = FM).
Soit H le point d'intersection de BD et CF.
Comme CHB et CBF sont droits, et BCH et BCF sont égaux, les triangles BCH et BCF sont similaires (demi triangle équilatéral) et BC = CF/2 = BF/sqrt(3), BH = BC/2 = BH/sqrt(3)...
tan(BCM) = BM/CB
tan(HCN) = HN/CH
Comme BCM = BCN = pi/3 - HCN, nous avons :
tan(pi/3 - HCN) = BM/CB
= (tan(pi/3) - tan(HCN)) / (1 + tan(pi/3)tan(HCN))
= (tan(pi/3) - HN/CH) / (1 + tan(pi/3)*HN/CH)
= (CH*tan(pi/3) - HN) / (CH + tan(pi/3)*HN)
=> BM*(CH + tan(pi/3)*HN) = CB*(CH*tan(pi/3) - HN)
=> BM*(CH + sqrt(3)*HN) = CB*(CH*sqrt(3) - HN)
Or CH = CB/2, BN = FM => BM = DN = HN+DH = HN+CH*sqrt(3)
donc nous avons :
BM*(CH + sqrt(3)*(BM-CH*sqrt(3))) = CB*(CH*sqrt(3) - (BM-CH*sqrt(3)))
=> BM*CH + BM*BM*sqrt(3) -3*BM*CH = CB*(2*CH*sqrt(3) -BM)
=> BM*BM*sqrt(3) -BM*CB = CB*CB*sqrt(3) -BM*CB
=> BM = CB
Surpenant : le point M est l'intersection du segment BF et du cercle de centre B passant par C et A (et symétriquement N par rapport à D).
Finalement, BM = FB-FM = CB = FB/sqrt(3)
donne x = FM/FB = 1-1/sqrt(3) soit presque 0,423
Merci pour vos énigmes.
 Bonjour Godefroy et merci pour cette enigme.
Bonjour Godefroy et merci pour cette enigme.
Ma réponse:
C'est Conrad qui aligne le premier les deux pigeons.
La fraction du trajet qu'ils ont accomplie est exactement
x=1-(racine(3)/3)
 bonjour,
bonjour,
si je ne me suis pas trompée dans mes calculs matinaux
*c'est C qui le premier a la possibilité de tirer les deux pigeons
ceux-ci ont alors parcouru à
par excés de leur parcours prévu(si ce parcours est bien FB pour l'un et BD pour l'autre)
si C rate son tire A a une chance de tirer les deux pigeons quand ils auront effectué 0,577 du parcours
si A rate aussi son tire les pigeons ont la vie sauve
merci
 Bpnjour Godefroy,
Bpnjour Godefroy,
Qui va remporter l'épreuve: le chevalier Conrad
Quelle proportion de leur trajet les pigeons auront-ils parcouru : 1-1/3* 3.
3.
Merci pour la joute.
 C'est Conrad qui va remporter la victoire en abattant simultanément les deux volatiles lorsque ceux ci auront effectués [((3^0.5)-1)/ (3^0.5) ]*100 % de leur parcourt
C'est Conrad qui va remporter la victoire en abattant simultanément les deux volatiles lorsque ceux ci auront effectués [((3^0.5)-1)/ (3^0.5) ]*100 % de leur parcourt
 Bonjour,
Bonjour,
Conrad va remporter l'épreuve
valeur exacte: x = 1 - ( 3) / 3
3) / 3
valeur arondie: x = 0,423
Merci pour l'énigme
 Étant en vacances, je propose une démonstration...
Étant en vacances, je propose une démonstration... 
J'ai pris les points A, B, C, D, E et F comme les racines 6ème de l'unité...
Donc ,
,
,
,
et
.
Soit .
Alors la droite (MC) a pour équation : .
Et la droite (BD) a pour équation : .
Le point N, intersection des deux droites (MC) et (BD) a pour abscisse et pour ordonnée
.
Enfin il faut que FM=BN, d'où l'équation à résoudre : .
On trouve alors .
Enfin on trouve x, en calculant : .
On trouve , ou encore avec 3 décimales x
 0,423.
0,423.
 Bonsoir à tous
Bonsoir à tous
sauf erreur c'est l'archer placé au sommet C qui l'emporte
donc le chevalier Conrad
pour
on a alors BM = BC
 Bonjour godefroy_lehardi,
Bonjour godefroy_lehardi,
Le baron Arnaud placé en A va remporter l'épreuve.
Les pigeons auront parcouru 0,605 du trajet.
 Salut,
Salut,
Le joueur qui tire la place E n'a vraiment pas de chance, il n'a aucune chance d'avoir les deux pigeons en une flêche.
Par contre, le joueur qui se mettra à la place A pourra (si son voisin de droite est mauvais  ) toucher les deux pigeons en tirant une flêche quand les pigeons auront parcouru 57.735% de leur trajet (ou 0.557u de distance).
) toucher les deux pigeons en tirant une flêche quand les pigeons auront parcouru 57.735% de leur trajet (ou 0.557u de distance).
Le plus chanceux est celui qui tirera la place C, il devra tant qu'à lui attendre que les pigeons parcourent 42.265% de la distance total (ou 0.423u de distance)
Enfin en résumé (en espérant ne pas mettre trompé) je dis donc :
C gagne , le pigeons auront fait 42.265% de leur trajet
A n'a plus qu'à attendre que C loupe son tire et devra tirer quand les pigeons auront fait 57.735%
E pourra aller cueillir des fleurs et regarder les pigeons voler, car ces chances de toucher les pigeons sont de 0.000% 
 Je dirais que seuls les arbalétriers en A et en C ont une chance de gagner.
Je dirais que seuls les arbalétriers en A et en C ont une chance de gagner.
-Pour l'arbalétrier en A, les deux pigeons sont alignés avec lui à x1=1-( 3)/3
3)/3
-Pour l'arbalétrier en C, les deux pigeons sont alignés avec lui pour:
x2=1/ 3
3
Or x1 x2
x2
Donc sauf erreur de ma part c'est l'arbalétrier positionné en C qui gagnera, excepté si il rate son tir, auquel cas l'arbalétrier en A aura alors sa chance.
L'arbalétrier en C gagnera pour x 0.423
0.423
Donc les pigeons auront parcourus 42,3% de leur trajet.
Clôture de l'énigme :
Pas de chance pour Arnaud !
J'ai été indulgent avec quelques étourdis qui ne lisent pas attentivement l'énoncé (n'est-ce pas dpi et torio ?) 
N'y voyez pas un assouplissement des règles mais plutôt l'expression de ma bonté naturelle dont il ne faudrait cependant pas abuser. 
 bonjour godefroy_lehardi
bonjour godefroy_lehardi
merci encore pour cette joute et l'indulgence pour les fautes d'orthographe,je viens de constater avec horreur que j'ai deux fois écrit tire au lieu de tir
 Comme gage pour dpi et torio, je propose qu'on les place en F et en B, qu'on les lâche en même temps, puis qu'on procède à la vérification expérimentale du résultat théorique de la joute...
Comme gage pour dpi et torio, je propose qu'on les place en F et en B, qu'on les lâche en même temps, puis qu'on procède à la vérification expérimentale du résultat théorique de la joute...

Bonsoir à tous,
si, comme le dit "Le Dino" on place dpi en F et Torio en B pour la vérification expérimentale, seul Torio sera atteint en N et dpi aura la grande chance d'échapper au carreau d'arbalète tiré depuis le point C.
Si mathématiquement la solution au problème posé est bien x=0,423, en réalité il est pratiquement impossible de réaliser l'exploit d'atteindre les 2 pigeons sauf si la vitesse du carreau est infinie.
Je m'explique: un bon chasseur doit d'abord anticiper le point d'impact avec le pigeon qu'il doit atteindre en N. Ensuite, en admettant que son carreau n'a pas été dévié par le choc, il faut un certain temps pour atteindre le second pigeon. On peut considérer que s'il a atteint le premier pigeon à la tête, le temps mis par le carreau entre N et M lui permettra de toucher le second pigeon au croupion.
Le temps du trajet du carreau entre M et N doit correspondre au temps mis par le second pigeon pour avancer de la longueur de son corps.
En pratique la vitesse initiale d'un carreau d'arbalète est de 102m/s ( environ 300 km/h)
la vitesse d'un pigeon de concours varie entre 60 et 120km/h. Si le pigeon mesure 30cm, il faudrait que la distance de N à M soit bien courte puisque le rapport des vitesses est de 5 à 3, trop faible
Bien à vous
 Du Poisson au pigeon
Du Poisson au pigeon
1/merci godefroy-lehardi pour ton indulgence =jamo²
2/je n'ai pas bien compris l'étourderie (dont je suis
pourtant un grand spécialiste)
*est-ce les 4 décimales au lieu de 3?
*est-ce car ma phrase ne précise pas que
c'est Conrad qui gagne,alors que cela me paraissait évident ?
3/pour le Dino et castoriginal
-épargnez deux pauvres pigeons qui pour une fois n'ont pas
mangé du poisson
Nombre de participations : 0
Temps de réponse moyen : 93:21:37.



