Inscription / Connexion Nouveau Sujet
Joute n°68 : Les nombres copains
Bonjour à tous,
Vous connaissez certainement les nombres amicaux (ou aimables ou amiables).
Si la somme des diviseurs propres d'un nombre entier X est égale à Y, et que la somme des diviseurs propres de Y est égale à X, alors on dit que X et Y forment un couple de nombres amicaux.
Nota : Les diviseurs propres d'un nombre X sont tous les nombres entiers naturels qui divisent X à l'exception de X lui-même.
Par exemple, 220 et 284 sont des nombres amicaux.
Mais les couples ont aussi des liens avec les autres sans que ça devienne forcément un ménage à trois (ou plus). Il existe donc des nombres entiers naturels qu'on appellera « copains » d'un couple de nombres amicaux.
Le nombre Z est un « copain » du couple de nombres amicaux (X, Y) si la somme des diviseurs propres de Z est égale à X ou à Y.
Par exemple, 562 est un copain du couple (220, 284) car la somme des diviseurs propres de 562 est égal à 284.
Question : Quel sont les couples de nombres amicaux inférieurs à 10 000 qui ont le plus de copains ?
Donnez-les tous avec la liste complète de leurs copains.

 Couple de nombres amicaux : (8128, 8128)
Couple de nombres amicaux : (8128, 8128)
Ils ont 27 copains :
6, 25, 28, 220, 284, 562, 496, 652, 1184, 1210, 1336, 1490, 1604, 1898, 2362, 2172, 2620, 2924, 3124, 5234, 5020, 5564, 6028, 6532, 6232, 6368, 8128
 Bonjour
Bonjour
D'après ce que je trouve, il n'y a que 5 couples de nombres amicaux en-dessous de 10.000.
Parmi ces cinq couples, celui qui a le plus de "copains" en-dehors du couple semble être (1184,1210).
Ses copains sont (en plus des deux membres du couple, bien sûr) :
1336
1490
1604
1898
2362
Merci pour la joute et à bientôt
(et bonne fête de Pâques !)
 Salut godefroy,
Salut godefroy,
Je propose le couple (1184,1210) dont les copains sont 1336, 1490, 1604, 1898 et 2362.
Merci.
 Bonjour,
Bonjour,
le couple de nombres amicaux inférieurs à 10 000 qui a le plus de copains est (1184,1210). Ils ont 5 copains, qui sont : 1336, 1490, 1604, 1898, 2362.
MErci beaucoup !
 Bonjour Godefroy,
Bonjour Godefroy,
Les couples de nombres amicaux inférieurs à 10 000 qui ont le plus de copains sont:
(1184,1210) et (1210,1184)
qui ont pour copains hormis les nombres des couples:
1336,1490,1604,1898,2362.
J'espère avoir bien compris la question !
 Bonjour,
Bonjour,
Je trouve 5 couples amicaux de nombres inférieurs à 10000.
(220, 284) : 1 copain
(1184, 1210) : 5 copains
(2620, 2924) : 3 copains
(5020, 5564) : 2 copains
(6232, 6368) : aucun copain (les pauvres)
Ma solution est donc :
Le couple (1184, 1210) qui a 5 amis : 1336 1490 1604 1898 2362
 Bonjour
Bonjour
Si j'ai bien compris la question le couple d'amicaux qui a le plus de copains est (1184,1210) ( ou (1210,1184)) dont les copains sont en dehors de 1184 et de 1210
1336, 1490, 1604, 2362
A+
 Ca sent le projecteuler
Ca sent le projecteuler  http://projecteuler.net/problem=21
http://projecteuler.net/problem=21
Je dirai donc 5 :
1210.
1184.
1336.
//
1210.
1184.
1490.
//
1210.
1184.
1604.
//
1210.
1184.
1898.
//
1210.
1184.
2362.
Pas sûr du tout de ma réponse en tout cas 
Scilab :
tic();
v=zeros(10000,1);
S=0;
for i=1:1:10000
if v(i)==0 then
v(i)=sum(diviseurs(i))-i;
end
if v(i)>i then
v(v(i))=sum(diviseurs(v(i)))-v(i);
if v(v(i))==i then
for C=1:10000
if v(i)<>C & i<>C then
if sum(diviseurs(C))-C == i | sum(diviseurs(C))-C == v(i) then
disp(v(i))
disp(i)
disp(C)
disp("//")
end
end
end
end
end
end
disp(toc());
 Bonsoir, Godefroy!
Bonsoir, Godefroy!
Comme il fallait s'y attendre, je ne trouve qu'un couple : (1184;1210).
Ce dernier a 7 copains (5 si on ne compte pas 1184 et 1210 eux-memes) qui sont: 1184, 1210, 1336, 1490, 1604, 1898 et 2362.
Par contre, j'ai un gros doute quant a l'unicite* (et meme la nature) du couple. Ceci vient du fait qu'il n'y a pas de restriction sur les copains a prendre en compte (sont-ils ou non inferieurs a 10000)... Ca m'a prit beaucoup de temps de verifier si cette solution restait (et restait unique) dans le cas ou on considererait aussi les copains plus grands que 10000. Je n'ai d'ailleurs pu le verifier que jusqu'a 30000, ce qui laisse encore un grand champ... Je pense neanmoins que la solution restera celle la (je l'espere, surtout!).
Bon, merci bien pour cette joute (pas evidente du tout). Est-il besoin de preciser que ce debit d'enigmes (3 en 3 jours!) est a conserver a tout prix? Du moins, a beaucoup de prix...
 Le couple amical inférieur à 10000 qui a le plus de copains est :
Le couple amical inférieur à 10000 qui a le plus de copains est :
(1184,1210).
Les copains sont : 1184,1210,1336,1490,1604,1898,2362
L'énoncé n'exclut les deux nombres composant le couple.. qui par définition sont copains du couple.
 Joyeuses PÄQUES
Joyeuses PÄQUES
Cette énigme n'est pas un cadeau
Sauf ommission voici les couples et leurs amis
pour certain du coté du mari pour d'autres de la femme...
220 7339 8131 8851
284 562
1184 1336 2362
1210 1490 1604 1898
2620 5234 7851
2924 2172 3124
5020
5564 6028 6525 7395
6232
6368 7455
 Voici ma réponse:
Voici ma réponse:
Ce sont les couples amicaux (1184 1210) et le symétrique (1210 1184) qui ont le plus de copains : 7 copains.
à condition de pouvoir considérer un membre du couple comme copain. Rien ne l'interdit dans l'énoncé.
On n'empêche pas non plus à X d'être égal à Y. Donc (6 6) est un couple amical.
(1184 1210) -> (1184 1210 1336 1490 1604 1898 2362)
(1210 1184) -> (1184 1210 1336 1490 1604 1898 2362)
(2620 2924) -> (2172 2620 2924 3124 5234)
(2924 2620) -> (2172 2620 2924 3124 5234)
(5564 5020) -> (5020 5564 6028 6532)
(5020 5564) -> (5020 5564 6028 6532)
(6232 6368) -> (6232 6368)
(6368 6232) -> (6232 6368)
(8128 8128) -> (8128)
(220 284) -> (220 284 562)
(284 220) -> (220 284 562)
(496 496) -> (496 652)
(6 6) -> (6 25)
(28 28) -> (28)
Nestor
 Bonjour godefroy et merci pour cette énigme bien sympa
Bonjour godefroy et merci pour cette énigme bien sympa 
Cependant certains points m'échappent :
- D'abord, tu n'as pas précisé dans quel intervalle se situe un copain. Car on peut aller jusqu'à l'infini, donc il faut bien poser une limite. Du coup moi je me suis limité à 100000, sinon c'est trop long à chercher pour mon programme.
- De plus, ta consigne suggère qu'il y a plusieurs couples amicaux qui ont le plus de copains. Or, moi je n'ai trouvé qu'un seul couple de nombres amicaux qui a le plus de copains. Donc il y a une contradiction. J'espère que je suis clair 
- Enfin, soit un couple de nombres amicaux (x;y). Est-ce que l'on doit également compter les cas où x=y ? Car il y a plusieurs couples dans ce cas.
Donc, étant donné que je ne suis sûr de rien, je vais être prudent.
J'ai trouvé que c'est le couple de nombres amicaux (1184;1210) qui a le plus de copains. J'en dénombre 5 (donc inférieurs à 100000) : 1336; 1490; 1604; 1898 et 2362.
Si jamais il fallait donner la liste complète des couples de nombres amicaux inférieurs à 10000 ainsi que tous leur copains, voir le tableau que j'ai réalisé en bas du message (j'ai compté les cas où x=y).
Voilà, j'espère que j'ai bon 
Méthode
D'abord j'ai cherché la liste des couples de nombres amicaux inférieurs à 10000 sans trop me fouler sur ce site : ![]() .
.
Et ensuite j'ai réalisé un petit programme en Python qui cherche les copains (inférieurs à 100000) d'un couple donné, dont voici le code :
origine1=input()
origine1=int(origine1)
origine2=input()
origine2=int(origine2)
nbr=1
while nbr<100000:
resultat=0
compteur=1
while compteur<nbr:
condition=nbr%compteur
if condition==0:
resultat+=compteur
compteur+=1
if resultat==origine1 or resultat==origine2:
print(nbr)
nbr+=1
Tout simplement 
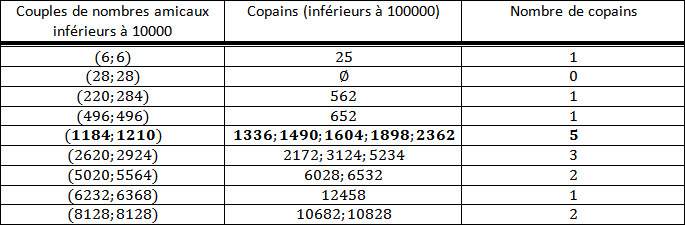
 Bonjour,
Bonjour,
| nb copains | nb copains | Amis | Copains | Copains | Copains |
| 5 | 2 | 1184 | 1336 | 2362 | |
| 3 | 1210 | 1490 | 1604 | 1898 | |
| ---- | |||||
| 3 | 1 | 2620 | 5234 | ||
| 2 | 2924 | 2172 | 3124 | ||
| ---- | |||||
| 3 | 0 | 5020 | |||
| 3 | 5564 | 6028 | 6532 | 30946969 = (5563²) | |
| ---- | |||||
| 2 | 0 | 220 | |||
| 2 | 284 | 562 | 80089 = (283²) | ||
| ---- | |||||
| 2 | 1 | 6232 | 12458 | ||
| 1 | 6368 | 40538689 = (6367²) |
détails:
| nb copains | nb copains | Amis | Copains | Copains | Copains | |||
| 2 | 0 | 220 | ||||||
| 2 | 284 | 562 | (2*281) | 80089 | (283²) | |||
| ---- | ||||||||
| 5 | 2 | 1184 | 1336 | (2^3*167 | 2362 | (2*1181) | ||
| 3 | 1210 | 1490 | (2*5*149) | 1604 | (2^2*401) | 1898 | (2*13*73) | |
| ---- | ||||||||
| 3 | 1 | 2620 | 5234 | (2*2617) | ||||
| 2 | 2924 | 2172 | (2^2*3*181) | 3124 | (2^2*11*71) | |||
| ---- | ||||||||
| 3 | 0 | 5020 | ||||||
| 3 | 5564 | 6028 | (2^2*11*137) | 6532 | (2^2*23*71) | 30946969 | (5563²) | |
| ---- | ||||||||
| 2 | 1 | 6232 | 12458 | (2*6229) | ||||
| 1 | 6368 | 40538689 | (6367²) |
et merci
 Bonjour,
Bonjour,
Apparemment c'est le couple (1184,1210) qui a le plus de copains.
Voici donc la liste de leurs 5 copains:
1236 et 2362 (dont la somme des diviseurs vaut 1184)
1490,1604 et 1898 (dont la somme des diviseurs vaut 1210)
Comme je ne comprends pas vraiment ce qui est exactement demandé comme solution (les paires??) Voici la liste des couples avec leurs amis respectifs.
(220,284): 562
(2620,2924): 5234,2172,3124
(5020,5564): 6028,6532
(6232,6368): -
 Le couple de nombres (1184;1210) est celui qui a le plus de copains, il en a 5 qui sont :
Le couple de nombres (1184;1210) est celui qui a le plus de copains, il en a 5 qui sont :
1336
1490
1604
1898
2362
Merci pour l'énigme !
 Bonjour godefroy_lehardi,
Bonjour godefroy_lehardi,
LE couple de nombres amicaux inférieurs à 10 000 qui a le plus de copains est (1184, 1210) avec 5 copains: 1336, 1490, 1604, 1898, 2362.
Le couple qui a le copain le plus grand est (6232, 6368) avec 12458 et 40538689 (carré du nombre premier 6367), mais ce n'était pas la question ... 
Merci pour la joute ! 
 Bonjour,
Bonjour,
Je vais me risquer à répondre à cette énigme :
Le couple (1184;1210) est formé de deux nombres amicaux et il possède plus d'amis que les autres, en tout 5 : 1336, 1490, 1604, 1898, 2362.
Mais alors je me suis posé bien des questions :
- Les nombres amicaux sont inférieurs à 10000. Et leurs amis : doivent-ils être aussi inférieurs à 10000 ?
- Est-ce qu'un couple peut être formé de nombres égaux (cas des nombres parfaits comme 28) ?
- Est-ce que l'on considère comme amis d'un couple les deux nombres amicaux eux-mêmes ? Ou bien les amis sont-ils distincts des nombres du couple ?
- "Les couples de nombres amicaux inférieurs à 10 000 qui ont le plus de copains" : il y a d'autres couples qui ont 3 ou 2 amis et donc qui ont plus d'amis que ceux qui en ont un seul ; faut-il les citer aussi ? J'ai décidé de citer le couple qui a le plus d'amis.
Merci!
 Après des tas de tests avec tableaux Excel de 40 000 Ko, voici ma réponse :
Après des tas de tests avec tableaux Excel de 40 000 Ko, voici ma réponse :
Le couple de nombres aimables inférieurs à 10 000 qui a le plus de copains est : 1184 & 1210. Leurs copains sont 1336, 1490, 1604, 1898 et 3636.
PS : C'est marrant comme définition des nombres aimables. Je la connaissais pas comme ça et du coup, j'étais parti dans une toute autre diréction... et c'était plus simple... ET EN FAIT NON !!
Bref...
Comment est-ce qu'il fallait raisonner pour que ce soit plus simple et pas autant à tatons ?
 Bonjour Godefroy,
Bonjour Godefroy,
Voici ce que mes meilleurs copains et moi avons trouvé :
- le couple de nombres amicaux inférieurs à 10 000 qui a le plus de copains est (1184;1210) avec 5 copains : 1336 , 1490 , 1604 , 1868 , 2362
- le couple (220;284) a 2 copains : 562 , 80089
- le couple (2620;2924) a 3 copains : 2172 , 3124 , 5234
- le couple (5020;5564) a 2 copains : 6028 , 6532
- le couple (6232;6368) a 1 copain : 12458
Merci à toi.
 Bonjour tout le monde
Bonjour tout le monde
- Les couples de nombres amicaux qui ont le plus de copains sont:
(220,284) qui ont pour copains 434 et 562
- Par contre les autres couples amicaux ont pour copains:
(1184,1210) " " 2362
(2620,2924) " " 5234
(6232,6368) " " 12458
(5020,5564) " " Aucun
 Bonjour,
Bonjour,
Pfiou, j'y ai passé un peu de temps quand même.
Je pense que le couple
(1184;1210)
a le plus de copains (5, sans compter 1184 et 1210 qui sont copains l'un de l'autre, évidemment), qui sont :
1336, 1490, 1604, 1898 et 2362.
Merci pour l'énigme,
Tof
 Bonjour,
Bonjour,
Voila ma réponse: (1184;1210)
Le couple (1184;1210) est un couple de nombres amicaux:
1184= 25*37 et s'(1184)= 1210
1210= 2*5*112 et s'(1210)= 1184
Ce couple a 5 copains, les voici:
1) 2362= 2*1181 et s'(2362)= 1184
2) 1604= 22*401 et s'(1604)= 1210
3) 1336= 23*167 et s'(1336)= 1184
4) 1490= 2*5*149 et s'(1490)= 1210
5) 1898= 2*13*173 et s'(1898)= 1210
Tous les autres couples de nb amicaux < 10000 ont au plus 3 copains.
Il existe 4 autres couples de nb amicaux < 10000 et voici la liste de tous leurs copains:
(2620;2924): ce couple a 3 copains
2620= 22*5*131 et s'(2620)= 2924
2924= 22*17*43 et s'(2924)= 2620
1) 5234= 2*2617 et s'(5234)= 2620
2) 2172= 22*3*181 et s'(2172)= 2924
3) 3124= 22*11*71 et s'(3124)= 2924
(5020;5564): ce couple a 3 copains
5020= 22*5*251 et s'(5020)= 5564
5564= 22*13*107 et s'(5564)= 5020
1) 30946969= 55632 et s'(30946969)= 5020
2) 6028= 22*11*137 et s'(6028)= 5564
3) 6532= 22*23*71 et s'(6532)= 5564
(220;284): ce couple a 2 copains
220= 22*5*11 et s'(220)= 284
284= 22*71 et s'(284)= 220
1) 80089= 2832 et s'(80089)= 284
2) 562= 2*281 et s'(562)= 284
(6232;6368): ce couple a 2 copains
6232= 22*5*11 et s'(6232)= 6368
6368= 22*71 et s'(6368)= 6232
1) 40538689= 63672 et s'(40538689)= 6368
2) 12458= 2*6229 et s'(12458)= 6232
Merci pour cette joute !
PS : la recherche des solutions est un peu laborieuse (surtout avec Excel) ...
On peut remarquer que la somme des diviseurs propres des nombres recherchés est pair (en effet tous les nb amicaux < 10000 sont pairs ...)
Par recurrence sur le nb de facteurs premiers (k) du nb recherché (a), on peut montrer que :
1- si a est pair (a1=2) 
 i > 1 tel que pi est impair
i > 1 tel que pi est impair
2- si a est impair (a1>2)  tous les pi sont pairs
tous les pi sont pairs
avec a= a1p1*…*akpk où les {ai;pi} forment la decomposition unique en facteurs premiers
Ensuite en utilisant que cette somme est necessairement < 6369 et on peut montrer que:
1- si a= est pair (a1=2)  k
k 5
5
2- si a est impair (a1>2)  k
k 2
2
où k est le nb de facteurs premiers de a
 Voici la liste des couples amicaux inférieurs à 10 000 et de leurs copains :
Voici la liste des couples amicaux inférieurs à 10 000 et de leurs copains :
couple (220;284)--> copains = 562, 80089
couple (1184;1210)--> copains = 1336, 1490, 1604, 1898, 2362
couple (2620;2924)--> copains = 2172, 3124, 5234
couple (5020;5564)--> copains = 6028, 6532, 30946969
couple (6232;6368)--> copains = 40538689
Le couple (1184;1210) est donc celui qui a le plus de copains avec 5
Ps : Merci d'avoir lancé cette énigme, ça m'a obligé à me remettre dans la programmation. 10 ans que je n'en avait pas fait !
 Bonjour,
Bonjour,
Dommage, si Godefroy_Lehardi avait demandé les copains de 6232 et 6368, plus d'un auraient oublié 40538689 = (6367²) ! (ou 12458 )
Ou encore :
Quel est le couple de nombre amicaux inférieurs à 15 000 qui a le plus de copains ?
Donnez le couple et le nombre de copains.
Réponse : 12285 et 14595 ont 143 + 140 = 283 copains
Je vous laisse chercher le nombre de copains de 1798875 et 1870245 !
 En fait suite à une petite erreur de programmation dont je m'étais aperçu aussitôt, j'ai mis la liste des copains de tous les couples amicaux.
En fait suite à une petite erreur de programmation dont je m'étais aperçu aussitôt, j'ai mis la liste des copains de tous les couples amicaux.
J'ai répondu 30s trop tôt...
 J'ai eu quelques frayeurs sur ce coup, mais bon... ce fut ne bonne joute.
J'ai eu quelques frayeurs sur ce coup, mais bon... ce fut ne bonne joute.
Petite precision a Gryfo: C'est vrai qu'il n'y a pas eu de precision sur les copains, mais ils sonst de toute facon limites. En fait, un nombre non premier ne peut etre copain avec un nombre inferieur a sa racine carree. Et un nombre premier n'est copain que de 1. Ceci dit, au dessus de 99980001, il n'existe forcement aucun nombre qui puisse etre copain d'un nombre inferieur a 10000!
Petite question pour dpi: Comment tu decides de qui est le mari et de qui est la femmee? Serieux, ca m'interesse, moi aussi je ''sexualise'' les nombres...
Nombre de participations : 0
Temps de réponse moyen : 101:12:35.


