Bonsoir tout de même

Si tu postais ton raisonnement qu'on vérifie ?

que les calcul ??

Non, le raisonnement et les calculs

1. a°) MA.MB=a
       MI+IA.MI+IB=a
       MI²+MI.IB+IA.MI+IA.IB=a
       MI²+MI.(IA+IB)+IA.IB=a
       MI²+MI.O+IA.IB=a
       MI²+IA.IB=a
       MI²-AI*IB=a
       MI²-IB*IB=a
       MI²-IB²=a
       MI²-AB²/4=a
donc MA.MB=MI²-AB²/4
    
   b°) 1-  MA.MB=-12
           MI²-AB²/4=-12
           MI²=-12+AB²/4
           MI²=-12+4/4
           MI²=-11  
           MI=racine carre de -11
       2-  de meme MI²=8+4/4
                   MI²=8+1
                   MI²=9
                   MI=racine carre de 9 soit 3  
  

2.  a°)   g(M)=k <==> AH.AB=k
         AM.AB=k <==> AH.AB=k
         AM.AB=k <==> AM.AB=k  car M est le projeté orthogonal de H sur (AB)

    b°)   AH.AB=k
          AH=AB/k   (j'esite avec k/AB )

    c°)  selon le b°) , on a

          AH=AB/k                        AH=k/AB

pour -12: AH=4/-12                       AH=-12/4
                                         AH=-3
pour 8:                              AH=4/8                                   AH=8/4          
AH=1/2                                   AH=2

je te dirai o fure et a mesure si tu veux

AM.MB=12
AM.AB=-6

AM.AB.MB=?????    JE SAIS PLUS

j'espere que je vais pouvoir avoir de l'aide merci

Bonsoir

AM.AM.MB n'a aucun sens, que veux tu calculer exactement ?

le reste c'est correcte ou pas

sinon je veux resoudre le systeme

quelqu'un peux m'aider svp

1)
a ° --> OK
---
2)

a°)
(en vecteurs)
AM.AB = (AH+HM).AB
AM.AB = AH.AB + HM.AB

HM.AB = 0 (puisque (HM) et (AB) sont perpendiculaires).

--> AM.AB = AH.AB

Et si g(M)=AM.AB = k, alors on a AH.AB = k
---
b°)
AH et AB sont colinéaires --> |AH|.|AB| = k
|AH|.4 = k
|AH| = k/4
---
3)
MA.MB=MI²-AB²/4.
MA.MB=MI²-4²/4.
MA.MB=MI²-4

MA.MB = 12 -->  MI² = 16
MI = 4
Et donc l'ensemble des points M qui convient pour avoir MA.MB = 12 est le cercle de centre I et de rayon 4. (1)

AM.AB=-6 est équivalent à AH.AB = -6
Avec AH et AB colinéaires --> H est dans [AB] et on a |AH| = 6/4 = 3/2
Donc le lieu de M est sur la perpendiculaire à [AB] passant par H sur [AB] et tel que |AB| = 3/2 (2)

Finalement les points M qui conviennent sont à l'intersection des lieux (1) et (2).
Il s'agit de 2 points ...
-----
Sauf distraction.  

pour le 3 j'ai pas tout a fait compris

lorsque l'on a (en vecteurs) AH.AB=k, est ce que l'on a le droit de faire :   AH=k/AB   (en vecteur) ??

*** message déplacé ***

Bonjours
Dans un systeme j'ai deux produits scalaire , mais je ne sais pas comment resoudre.
On a:   MA.MA=12
        AM.AB=-6   (en vecteur)

*** message déplacé ***

schumileboss,
à lire et à respecter, merci

extrait de la FAQ du forum :

Q03 - Pourquoi ne faut-il pas faire du ''multi-post'' ?

Pour de nombreuses raisons.

Pour mémoire, le multi-post consiste à reposer une même question dans un sujet différent , ou à poser des questions successives d'un même problème dans des sujets différents.

De même, une demande identique sur plusieurs sites sera considérée comme un multipost et la discussion pourra être fermée par un modérateur.

Etant donné tous les désagréments créés par le multi-post, le non-respect de cette règle entraînera votre exclusion temporaire ou définitive du forum !

Voici maintenant quelques raisons qui font que nous combattons avec autant d'ardeur le multi-post (et ses adeptes ) :

• La perte de temps pour les modérateurs qui consacrent leur temps bénévolement pour garantir la qualité des sujets et des échanges sur le forum.
• Le respect du travail des correcteurs qui consacrent leur temps bénévolement pour aider ceux qui sollicitent de l'aide.
• La lisibilité du forum de manière à ce qu'un sujet ayant déjà reçu de l'aide soit facilement identifié et qu'un sujet n'en ayant pas encore reçu puisse à son tour en recevoir.

Rappelez-vous une nouvelle fois la règle d'or du forum :
1 sujet créé = 1 problème

Ta question:

"lorsque l'on a (en vecteurs) AH.AB=k, est ce que l'on a le droit de faire :   AH=k/AB   (en vecteur) ??"

Généralement, Non.

Mais ici, on est dans un cas particulier.
A, B et H sont alignés est donc, non seulement on a:

vect(AH).vect(AB) = k

Mais aussi |AH|.|AB| = k

Et donc |AH| = k/|AB|

...
-----

a ok

mais pour le systeme j'ai rien piger du tout

svp de l'aide pour resoudre un systeme

En vitesse, et je suis souvent distrait ...

est un produit scalaire, son résultat est donc un nombre (pas un vecteur).

Il a été montré au début que:



Or
Pareillement:



Et avec , il vient donc:





C'est à dire la distance |MI| = une constante (cette constante = 4).
Donc M doit se trouver n'importe où à une distance de 4 du point I.
M est donc sur un cercle de centre I et de rayon 4. (Et alors on a )
-----
Mais il faut aussi que :
, c'est une seconde contrainte.
D'après le point 2a, on a montré que.

était équivalent à

Donc est équivalent à

Mais comme A, B et H sont alignés -> angle(AHB) = 0 ou 180 degrés, on a:

(180 degrés imposé par le signe - du -6)







Et M est par hypothèse sur la perpendiculaire à (AB) passant par H.

Contrairement à ce que j'avais dit, H est sur (AB) tel que |AH| = 3/2, mais H est à l'extérieur de [AB], (à cause de l'angle 180 degrés précédent).

Donc M est sur la perpendiculaire à (AB) passant par H avec la position de H précisée ci-dessus.
-----
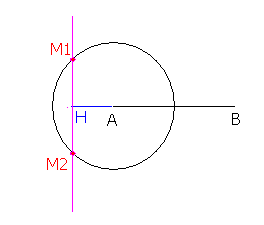
M doit donc être à la fois sur le cercle de centre I et de rayon 4 et sur la pependiculaire à (AB) décrite ci-dessus.

Les positions possibles pour M pour satisfaire le systèmes sont donc les points d'intersection du cercle de centre I et de rayon 4 et de la pependiculaire à (AB) décrite ci-dessus.

Cela devrait se résumer en 2 points.
------
A vérifier ...