Inscription / Connexion Nouveau Sujet
Longueurs autour d'un triangle (problème réel, pas un exo)
Salut à tous,
Voici une semaine que je m'arrache les cheveux sur ce problème sans succès :
On connait les longueurs (a,b,c) et on cherche (e,f,g). (e,f) peut être vu comme des coordonnées cartésiennes.
J'ai commencé par la méthode naïve :
- Avec de la trigo ou du Thalès, on obtient les rapports (linéaires) entre les sous triangles du haut et du bas.
- Avec du Pythagore, on trouve deux équations (quadratiques), par exemple : a² = (g + 2e)² + f²
Autant Mathematica que moi coinçons sur la résolution du système.
J'ai ensuite été voir du coté des coordonnées homogènes sans beaucoup plus de succès :
- Droites normalisées (facteur 1/longueur) :
da:, db:
, dc:
Calculer les intersections à coup de produit vectoriel permet d'introduire la longueur c mais il me manque des équations.
Le plus gros problème tient au fait que les 3 inconnues (e,f,g) sont étroitement liées aux données (a,b,c) de sorte que je ne trouve pas de méthode pour "résoudre comme on dessinerait".
La moindre suggestion est la bienvenue.
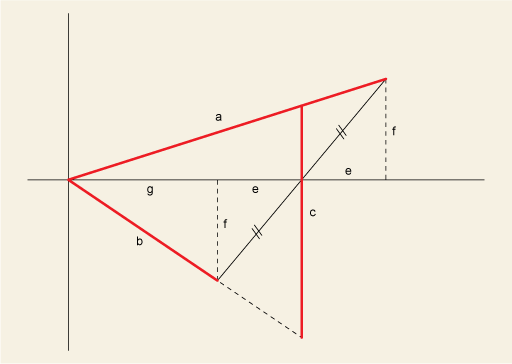
Désolé, je reformule :
Dans un repère orthonormé (O,x,y), deux points A et B.
(O,x) coupe (AB) en son milieu M tel que AM = MB
La droite passant par M et parallèle à l'axe (O,y) coupe les droites (OA) et (OB) en C et C' respectivement.
OA = a, OB = b, CC' = c
On cherche :
- les coordonnées cartésiennes (e,f) des vecteurs BM=MA
- la position de M sur (0,x)
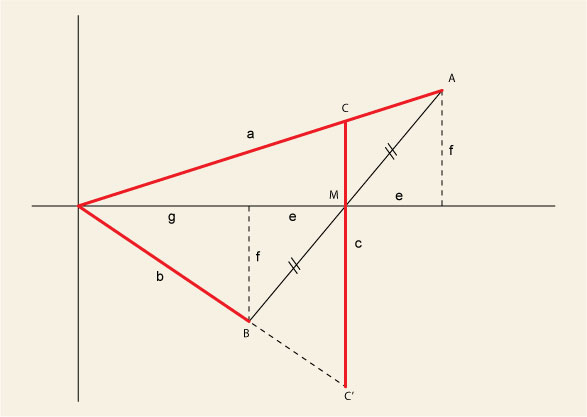
bonjour,
comme M est le milieu de BA tu peux peut être utiliser le théorème de la médiane
OA²+0B²=AB²/2 +2OM²=2BM²+20M²
soit a²+b²=2(e²+f²)+2(g+e)² (1)
on a aussi (2)(g+e)²+f²=a²
tu peux calculer CM
CM/f=(g+e)/(g+2e) tu en déduis MC' et f/MC'=g/(g+e) (3)
ce n'est pas très élégant et je ne sais pas si cela aboutit
sauf erreur de ma part la (3) permet d'exprimer f à l'aide de g et e
je trouve( sans aucune garantie)
f=gc(g+2e)/(2e(g+e))
Merci pour la piste de la médiane.
Ton équation (2) est fausse :
(2a)
(2b)
Donc avec le théorèmes de la médiane, on a :
(1)
Avec (2b), on substitue dans (1)
Notez qu'en utilisant (2a) au lieu de (2b), on obtient le même résultat.
En résolvant , on obtient:
(3)
Appliquant Thalès dans les triangles OAM et OBM, on pose :
(4)
Substituant de (3) dans (4), on obtient :
On resout et
:
Et je coince.
Une idée ?


 géométrie en post-bac
géométrie en post-bac