Inscription / Connexion Nouveau Sujet
Nombres complexes
Bonjour,
Voici mon DM, quelqu'un peut voir si c'est juste ce que j'ai fait et m'aider sur les questions où je bloque?
*Sylvieg>Énoncé reconstitué dans une des réponses  *
*
Dans le plan complexe muni d'un repère orthonormé direct (O;u,v), (unités 2cm).
1) Placer A et B les points d'affixes -i et 3i
Voir figure jointe
Et soit f la transformation qui, à tout point M du plan, d'affixe z, M différent de A, associe le point M' d'affixe z' telle que z'=(iz+3)/(z+i)
2)a) Résoudre l'équation f(z) = z
f(z) = z <--> (iz+3)/(z+i) = z <--> iz+3 = z(z+i) <--> iz+=z²+iz <-->z²-3=0 <--> z1= racine carrée de 3 ou -racine carrée de 3.
b) Donner les formes trigonométrique et exponentielle des éventuelles solutions de l'équation f(z)=z ci-dessus.
Iz1I = racine carrée de 3
arg(z1) = (u;OM1)=0
Donc z1= racine carrée de 3(cos 0 + i sin 0) <--> z1 = racine carrée de 3 * e^(i*0)
Iz2I = racine carrée de 3
arg(z2) = (u;OM2) = pi
Donc z2= racine carrée de 3 (cos pi + i sin pi) <--> z2 = racine carrée de 3 * e^(i*pi)
c) En déduire que f admet deux points invariants appartenant au cercle (C) de diamètre [AB] et placer ces 2 points sur un graphique.
Soit E le centre du cercle (C) de diamètre [AB]. On a :
AE= EB =1/2 AB = 1/2 IzB - zAI = 1/2 I3i-(-i)I = 1/2 I4iI = 4/2 = 2
Soit E(xE;yE)
AE = [(xE-0)² + (yE+1)²]^(1/2) = 2 <--> xE² +( yE+1)² = 4
Sachant que A et B appartiennent à l'axe des ordonnées et que E est le milieu de [AB] alors E appartient aussi à l'axe des ordonnées d'où xE=0.
Donc: (yE+1)²=4 <--> yE+1 = 2 ou -2
* Si yE+1 = 2 alors yE = 1 d'où E(0;1)
* Si yE + 1 = -2 alors yE = -3 d'où E(0;-3) et dans ce cas, E n'appartient pas à [AB], donc ce cas est refusé.
On a alors, zE = i.
Soit M1 et M2 deux points d'affixes respectives z1 et z2.
M1(racine de 3;0) et M2(-racine de 3;0)
EM1= Iz1 - zEI = Iracine de 3 - iI = 2
Donc [EM1] est un rayon du cercle (C). On en déduit que M1 appartient à (C).
De même EM2 = 2 donc M2 appartient à (C).
Et comme f(z)=z pour tout point M d'affixe z alors: f(z1) = z1 et f(z2)=z2. Donc M1 et M2 sont deux points invariants de (C).
Je ne suis pas sûre de ma réponse et je me demande s'il n'y a pas une autre méthode plus courte.
d) On note C le point d'affixe c=-2+i, montrer que C', image de C par f, est sur l'axe des abscisses.
C(-2;1)
c'= (ic+3)/(c+i) = (i(-2+i)+3)/(-2+i+i) = -1 (après plusieurs étapes de calculs). Donc C'(-1;0). On en déduit que C' est sur l'axe des abscisses.
3) Pour tout z différent de -i, on considère le nombre complexe w=(z-3i)/(z+1)
a) Montrer que pour tout z différent de -i, on a z'=i*w
j'ai calculé i*w en remplaçant w et j'ai trouvé z'
b) En déduire que pour tout point M différent de A et B, arg(z')=(MA,MB) + pi/2 à 2 pi près (MA et MB en vecteurs comme u, v )
arg(z')=arg(i*w) = arg(i) + arg(w) + 2k pi (k?Z) = arg(zE)+arg(w)+2k pi = (u;OE)+arg(w)+2k pi = (pi/2)+arg(w)+2k pi
Or, arg(w)=arg[(z-3i)/(z+i)] = arg(z-3i)-arg(z+i)+2k' pi (k'?Z)
arg(w) = arg(z-zB)-arg(z-zA)+2k' pi = (u;BM)+(u;MA)+2k' pi = (MA;MB)+2k' pi
Donc arg(z')=(pi/2)+(MA;MB)+2k' pi = (MA;MB)+(pi/2)+2K pi (K=k+k' ?Z)
(Là aussi u; OE; MA; MB; BM sont des vecteurs et je ne suis pas du tout sûre de mes calculs)
c) En déduire l'ensemble des points M d'affixe z tels que z' soit imaginaire pur.
z' est imaginaire pur <--> arg z' = pi/ ou - pi/2
DOnc (MA; MB)+pi/2+2K pi = pi/2 ou -pi/2 <--> (MA;MB)+2K pi = 0 ou -pi
* Si (MA;MB)+2K pi = 0 alors M se trouve sur l'axe des ordonnées avec M n'appartient pas à [AB]
* Si (MA;MB)+2K pi = -pi alors M se trouve sur l'axe des ordonnées avec M?[AB]
On en conclut que l'ensemble des points M d'affixe z tels que z' soit imaginaire pur est l'axe des ordonnées avec A et B exclus
(Là encore je ne suis pas sûre)
d) Soit M un point du cercle de diamètre [AB] privé des points A et B, à quel ensemble appartient le point M'?
Je bloque à cette question, j'ai juste fait: M?C <--> z=2
4)a) Montrer que pour z différent de -i, on a Iz+iI*Iz'-iI=4 (exprimer z'-i en fonction de z)
Pas de problème pour cette question, j'ai bien trouvé 4
b) En déduire que si M(z) appartient au cercle de centre A et de rayon 2 alors M'(z') appartient à un cercle dont on déterminera le centre et le rayon.
(Je bloque aussi pour cette question, je ne sais pas comment raisonner)
Merci pour votre aide 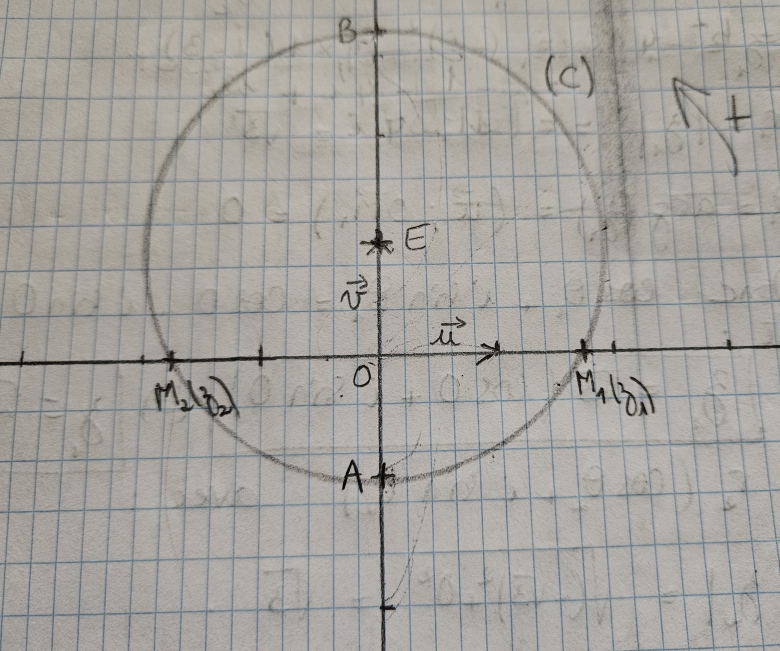
salut
extrêmement illisible : je t'invite pour tes prochains sujets de :
1/ recopier l'énoncé dans son intégralité (et seulement l'énoncé)
2/ recopier au dessous tes réponses (et pas besoin de rouge)
la racine carrée s'obtient avec l'icone  (à droite de l'icone X2
(à droite de l'icone X2
2c/ : on te demande "en déduire" : les points invariants ont pour affixes les solutions de l'équation f(z) = z donc il n'y a rien à faire
3b/ c'est plutôt pour tout z différent de -1 et qui est E ?
Bonjour,
J'ai reconstitué l'énoncé :
Dans le plan complexe muni d'un repère orthonormé direct (O;u,v), (unités 2cm).
1) Placer A et B les points d'affixes -i et 3i
Et soit f la transformation qui, à tout point M du plan, d'affixe z, M différent de A, associe le point M' d'affixe z' telle que z'=(iz+3)/(z+i)
2)a) Résoudre l'équation f(z) = z
b) Donner les formes trigonométrique et exponentielle des éventuelles solutions de l'équation f(z)=z ci-dessus.
c) En déduire que f admet deux points invariants appartenant au cercle (C) de diamètre [AB] et placer ces 2 points sur un graphique.
d) On note C le point d'affixe c=-2+i, montrer que C', image de C par f, est sur l'axe des abscisses.
3) Pour tout z différent de -i, on considère le nombre complexe w=(z-3i)/(z+1)
a) Montrer que pour tout z différent de -i, on a z'=i*w.
b) En déduire que pour tout point M différent de A et B, arg(z')=(MA,MB) + pi/2 à 2 pi près (MA et MB en vecteurs comme u, v )
c) En déduire l'ensemble des points M d'affixe z tels que z' soit imaginaire pur.
4)a) Montrer que pour z différent de -i, on a Iz+iI*Iz'-iI=4 (exprimer z'-i en fonction de z)
b) En déduire que si M(z) appartient au cercle de centre A et de rayon 2 alors M'(z') appartient à un cercle dont on déterminera le centre et le rayon.
Désolée, je pensais bien faire en séparant les questions de mes réponses et je pensais que ça allait être plutôt plus clair en ajoutant des couleurs. Je le saurai pour la prochaine fois.
Le point E, je l'ai dit dans mon corrigé, c'est le centre du cercle (C) de diamètre [AB].
Je ne comprends pas pour la 2)c) faut-il juste dire que les points invariants de (C) sont les points vérifiant f(z)=z et donc ce sont les deux solutions trouvées en 2)a)?
Pour la 3) j'ai bien z différent de -i et non pas -1.
Merci de me répondre pour les autres questions et de m'éclairer plus.
Kamichi, si tu veux poursuivre sur notre site, tu vas aller supprimer ton énoncé de l'autre côté, ou au moins dire que tu n'as plus besoin d'aide.
3) Pour tout z différent de -i, on considère le nombre complexe w=(z-3i)/(z+1)
3) Pour tout z différent de -i, on considère le nombre complexe w=(z-3i)/(z+1)
Je n'ai pas compris: pourquoi remplacer z par -1? Et c'est pour répondre à la question 3)b) cette remarque?


 ) :
) :

