Inscription / Connexion Nouveau Sujet
produit scalaire
Bonjour à tous,
J'ai un autre exos sur les produits scalaires :
Soient vecteur u et vecteur v quelconques
1) Démontrer que : norme u^2 +norme v^2 = 1/2 [(norme u+v^2 )+ norme u-v^2)]
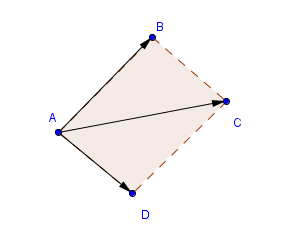
2) Soit ABCD un parallélogramme quelconque. Déduire de la question précédente la relation suivante : AB^2 + AD^2 = (AC^2+BD^2)
Démontrer alors la relation suivante : AB^2 + BC^2+ CD^2+ DA^2= AC^2+BD^2
3) On considère un parallélogramme ABCD tel que AB =3 et AC=6 Quelle est la longueur BC ?
4) On considère un losange de côtés 4 et dont une diagonale a pour longueur 5. Quelle est la longueur de l'autre diagonale ?
Merci de votre aide
La norme c'est une valeur absolue qui permet de mesurer la longueur de toutes les représentations d'un vecteur dans l'espace. C'est la bonne définition ?
Ok, donc si tu connais cette formule :
(1)
donc
et finalement (*)
Tu as le premier gros morceau. Maintenant, il te faut aussi
C'est facile, il suffit de remplacer par
dans la formule (1)
Vas-y 
je trouve : vecteur u. - vecteur v = 1/2 ( norme vecteur u- vecteur v ^2) - norme vecteur u^2 - norme vecteur - v^2
Si tu as essayé, tu trouves quoi ? Bizarre ton explication ...
Sinon, c'est bien, mais il faut simplifier :
Finalement :
donc (**)
Effectivement, il faut mettre en relation les expressions (*) et (**)
Qu'est-ce qu'il suffit de faire pour avoir l'égalité demandée ?
Je suis un peu bloquée car je ne sais pas trop quoi faire des -2\vec{u}.\vec{v} et 2\vec{u}.\vec{v}

bonjour
si on passe uniquement par la définition de la norme on peut calculer =a²+c²-2ac+b²+d²-2bd
=a²+c²+2ac+b²+d²+2bd
c'est juste iderden?
Merci Iderden de votre aide. Du coup il me reste (norme vecteur u+v ^2) + (norme vecteur u-v ^2) = (norme vecteur u)^2 + (norme vecteur v)^2 + (norme vecteur u)^2 + (norme vecteur v)^2 et la je ne sais pas quoi faire
bonjour sarah974 : su tu les regroupes et que tu multiplies par 1/2 tu obtiens l'égalité demandée.
Non?
Oui sarah , c'est ce qu'il faut voir.
Dans la formule du 1), qui s'appelle l'identité du parallélogramme, les vecteurs et
sont quelconques.
Donc est ce que je peux dire soit norme vecteur u^2 associé a AB^2 et norme vecteur v^2 associé a AD^2. Par relation, norme vecteur u+v ^2 = AB^2+AD^2
= AC^2
Il suffit d'écrire en remplaçant :
Puisque est un parallélogramme,
se simplifie (règle du parallélogramme) ainsi que
(il faut écrire ça autrement).
Ah oui d'accord pour la suite j'ai trouvé ça quand on me demande de démontrer :
vecteur AB^2+ vecteur AD^2 = 1/2 (AC^2 + BD^2)
je multiplie tout par 2
vecteur AB^2 + vecteur AB^2+ vecteur AD^2+ vecteur AD^2 = AC^2 + BD^2
Or dans un parallélogramme, les côtés opposées sont parallèles.
donc AB^2 = CD^2 et AD^2= BC^2
vecteur AB^2 + vecteur BC^2 + vecteur CD^2 + vecteur AD^2 = AC^2 + BD^2
Est ce que ma démonstration est bonne ?
Tu veux démontrer :
vecteur AB^2+ vecteur AD^2 = 1/2 (AC^2 + BD^2)
et tu arrives à :
vecteur AB^2 + vecteur BC^2 + vecteur CD^2 + vecteur AD^2 = AC^2 + BD^2
Donc tu n'as pas démontré ce qu'on voulait

De plus, dans ton raisonnement, ce n'est pas le fait que les côtés opposés soient parallèles qui est utile ici, mais que les côtés soient égaux deux à deux, et donc que la norme des vecteurs opposés deux à deux soient égaux.
Mais bon, dans le parallélogramme
Ensuite,
Donc si je continue votre égalité, \vec{AB}|-\vec{AD}=\vec{AB}+\vec{DA}=\vec{DA}+\vec{AB}=\vec{AC}.
Et pour obtenir \vec{BD} est ce qu'on peut dire que les diagonales se coupent en leurs milieux donc elles sont égales et que la norme des vecteurs opposées deux à deux sont égaux ?
Tu fais compliqué ^^
Oui, c'est bien la relation de Chasles.
Donc
Donc (*)
Il faut que tu regardes ce dont tu as besoin dans la formule que tu veux prouver.
Pour l'autre, par la règle du parallélogramme :
Donc (**)
Il n'y a plus qu'à remplacer les résultats trouvés lignes (*) et (**).
Je suis désolée mais je me suis un peu embrouillée et mal exprimée, enfaite je voulais démontrer AB^2+ BC^2 + CD^2 + DA^2 = AC^2+ BD^2. Donc est ce que mon ancienne démonstration est à peu près correcte ?
 Oui, c'est bon. Fais juste attention qu'on invoque l'égalité des longueurs des côtés opposés deux à deux.
Oui, c'est bon. Fais juste attention qu'on invoque l'égalité des longueurs des côtés opposés deux à deux.
D'accord merci. pour le 3) j'ai appliqué la formule suivante : AB^2+ AD^2 = 1/2 (AC^2 + BD^2)
et j'ai trouvé que AD = racine de 27 et par conséquent comme les cotés sont égaux deux à deux AD = BD donc BD= racine de 27
Regarde le schéma : on n'a pas AD=BD, mais AD=BC.
On ne te donne pas la longueur BD ? On ne te donne que deux longueurs ?
Ah non, ça ne va pas. Si les diagonales ont même longueur, alors ABCD est un rectangle, et inversement.
Or, on ne précise rien de spécial sur ABCD ...
Ah il ne peux pas avoir les mêmes longueurs ? Donc la comment je peux savoir la mesure de BD ? pour pouvoir trouver BC ?
Pour la 4), j'ai appliqué la même formule que plus haut : AB^2+ AD^2 = 1/2 (AC^2 + BD^2). j'ai remplacé AB par 4, AD par 4 et AC par 5. et je trouve que BD = racine de 39
Lorsque que j'ai remplacé mes resultats obtenue pour la 3) dans la formule AB^2 + BC^2+ CD^2+ DA^2= AC^2+BD^2 je trouve le même résultat des deux cotés de l'égalité donc mon résultat est juste non ?

Il manque une donnée pour la 3).
De toute façon, avec deux longueurs, tu ne peux même pas définir un triangle : il te faut la troisième longueur ou l'angle entre et
.
...