Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths spé AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau maths spé
Partager :

Série n*x^n

Posté par
theboss1er 28-06-09 à 12:26

Bonjour,

je n'arrive pas à exprimer la somme de cette série : 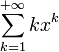Série n*x^n

Peux-t-on le faire directement, sans questions intermédiares ??

Merci d'avance

a++

Posté par
gui_toure : Série n*x^n 28-06-09 à 12:28

Saloute theboss1er,

Reconnais une dérivée quelque part

Posté par
amauryxiv2re : Série n*x^n 28-06-09 à 12:29

Tu mets x en facteur, et tu intègres .... Ca porte sur les séries entières, je suppose.

Posté par
theboss1erre : Série n*x^n 28-06-09 à 12:35

oui effectivement

Merci !!

Pour ceux que ça intéresse : Série n*x^n

a+

Posté par
ottore : Série n*x^n 28-06-09 à 15:45

Il faut quand même justifier que tu as le droit.
Suivant ton avancement dans l'année, c'est plus ou moins évident...

Posté par
theboss1erre : Série n*x^n 28-06-09 à 16:41

vu qu'on est dans l'intervalle de convergence on a convergence normale

Posté par
elhor_abdelali Correcteurre : Série n*x^n 29-06-09 à 12:11

On peut aussi le montrer de la maniére (élémentaire) suivante : pour n\in\mathbb{N}^* et z\in\mathbb{C} on a ,

4$\fbox{(1-z)\Bigsum_{k=1}^nkz^k=\Bigsum_{k=1}^nkz^k-\Bigsum_{k=1}^nkz^{k+1}=\Bigsum_{k=1}^nkz^k-\Bigsum_{k=1}^{n+1}(k-1)z^k=\Bigsum_{k=1}^nz^k\;-\;nz^{n+1}}

d'où si z\neq1 on a 4$\fbox{\Bigsum_{k=1}^nkz^k=\frac{z-z^{n+1}}{(1-z)^2}\;-\;\frac{nz^{n+1}}{1-z}=\frac{z}{(1-z)^2}\;-\;(n+1)z^{n+1}\frac{1-\frac{n}{n+1}z}{(1-z)^2}}

et on voit bien que si 3$\blue\fbox{|z|<1} on a 5$\red\fbox{\Bigsum_{k=1}^{+\infty}kz^k=\frac{z}{(1-z)^2}} sauf erreur bien entendu



remarque : la fonction z\to\frac{z}{(1-z)^2} est définie (voir même analytique) sur tout l'ouvert \mathbb{C}-\{1\}

alors que le domaine de convergence de la série entière \Bigsum_nnz^n n'est que le disque unité ouvert de \mathbb{C} .

Posté par
theboss1erre : Série n*x^n 03-07-09 à 00:40

Preuve très élégante Bravo !

Concernant la remarque, est-ce ceci que l'on appelle "prolongement analytique" ?

Posté par
ottore : Série n*x^n 03-07-09 à 01:01

Le prolongement analytique est quelque chose d'un peu compliqué à définir, mais grosso modo si tu as une fonction analytique f définie sur un domaine D et une fonction analytique g définie sur un domaine D' et que sur D inter D' f et g coincident, on dit que g est un prolongement analytique de f sur D'.

Posté par
elhor_abdelali Correcteurre : Série n*x^n 03-07-09 à 02:27

avec les notations de otto (que je salue ) si on note f la somme de la série entiére \Bigsum_{n\ge1}nz^n , D le disque unité ouvert de \mathbb{C}

g la fonction z\to\frac{z}{(1-z)^2} et D^'=\mathbb{C}-\{1\} on a :

- f holomorphe (donc analytique) sur D

- g holomorphe (donc analytique) sur D^'

- f=g sur D

donc oui : g est le prolongement analytique de f à \mathbb{C}-\{1\} sauf erreur bien entendu

Posté par
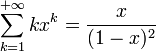
theboss1erre : Série n*x^n 03-07-09 à 10:44

Merci bien


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !