Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... BTSForum de maths BTS AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau BTS
Partager :

suite

Posté par
macene 23-01-09 à 21:18

bon soir alors j'essay de montrer que 0Un3  sachant que Un+1=2Un+3/Un+2  bon j'arrive a le faire mais avec une methode apparament fausse donc voila
et encore merci pour votre aide

Posté par
macenere : suite 23-01-09 à 21:39

j'ai utilisé la recurrence mais en vains le probleme est du genre 610
                      15
                 donc 62
ce qui est faut bien sur ce n'est pas les resultats que j'ai trouvé mais le probleme est dans le ganre cité ci dessus voila et merci pour toute aide

Posté par
dhaltere : suite 23-01-09 à 22:11

1) utilise les parenthèses. Ton expression est erronée.
2) donne la valeur initiale. Sinon ton énoncé est faux dans certains cas.

Posté par
macenere : suite 23-01-09 à 22:16

bon on me demande de montrer que
0(Un)n3
sachant que Un+1=(2Un+3)/(Un+2)

voila si sa peut t'aider comme ça sinon je voudrais bien que tu sois précis et methodique dans ta démonstration et encore merci

Posté par
dhaltere : suite 23-01-09 à 22:25

Commence par l'être toi-même, précis. Tu n'as toujours pas donné la valeur initiale et tu voudrais qu'on soit "précis et méthodique" ?

Je te signale que même accompagnée de tes remerciements, ta requête est blessante.

En ce qui me concerne, et je crois que l'ensemble du site est assez clair à ce sujet, je veux donner à des gens comme toi des conseils pour qu'ils puissent avancer, pas leur rédiger leurs corrigés en restant "précis et méthodique".

Bonne soirée.

Posté par
macenere : suite 23-01-09 à 22:31

dsl si t'as mal prie ma reponse mais le but n'etait pas de t'enfoncer au contraire j'ai reformuler le msg en mettant des paranthese comme tu l'as demander et en te demandant d'etre précis c'est juste pour savoir quelles sont les étapes par ou tu passess et voir ou est mon erreur mais bon ça ne fait rien bonne nuit

Posté par
toriore : suite 24-01-09 à 13:57

f(x) = (2x+3)/(x+2)

On remarque que  f(x) est strictement croissante.
et que f(0) = 1,5
f( rac(3) ) = rac(3)

donc si  0 <=x < rac(3)  on a  1,5 <= f(x) < rac(3)

Posté par
macenere : suite 24-01-09 à 23:02

merci beaucoup

Posté par
dhaltere : suite 25-01-09 à 12:42

Comme personne n'a relevé cette énormité, je reprends la main.
J'espère que tu pourras en profiter.

On a d'une part une fonction
f(x)=\frac{2x+3}{x+2}
Son domaine de définition est \mathbb{R}-\{-2\} = ]-\infty ; -2[ \cup ]-2;+\infty[
Il est vrai qu'elle est croissante sur ]-\infty ; -2[ et aussi sur ]-2;+\infty[
Il est vrai que f(0)=\frac32
Mais la réponse de torio confond u_n et f(n)

On n'a pas u_0=f(0) :
la fonction f() sert à déterminer la relatin de récurrence entre u_n et u_{n+1}

u_{n+1}=f(u_n) et non pas :
FAUX : u_n=f(n)

Si u_0>\sqr3 alors u_n est décroissante et u_n>\sqr3.
Si u_0<-\sqr3 alors u_n est d'abord décroissante, puis croissante, puis décroissante, et à partir de ce moment, u_n>\sqr3.
Si u_0=-\sqr3 ou u_0=\sqr3, alors u_n est constante.

Voilà pourquoi je te demandais la valeur initiale de la suite.

Nous supposerons alors
-\sqr3<u_0<\sqr3

Alors nous montrons par récurrence que pour tout n, -\sqr3<u_n<\sqr3

L'astuce est de décomposer f(x)=\frac{2x+3}{x+2}=\frac{2(x+2-2)+3}{x+2}=2-\frac1{x+2}

Propriété d'initialisation de la démonstration de récurrence
-\sqr3<u_0<\sqr3

Hypothèse de récurrence :
si c'est vrai pour n :
-\sqr3<u_n<\sqr3
montrons que c'est vrai pour n+1

-\sqr3<u_n<\sqr3

2-\sqr3<2+u_n<2+\sqr3
on a 0<2-\sqr3<2+u_n donc on peut prendre l'inverse. Attention : changement du sens des inégalités
\frac1{2-\sqr3}>\frac1{2+u_n}>\frac1{2+\sqr3}
on prend l'opposé : rechangement du sens des inégalités
-\frac1{2-\sqr3}<-\frac1{2+u_n}<-\frac1{2+\sqr3}
On ajoute 2
2-\frac1{2-\sqr3}<2-\frac1{2+u_n}<2-\frac1{2+\sqr3}
On simplifie
\frac{3-2\sqr3}{2-\sqr3}<\frac{2u_n+3}{u_n+2}<\frac{3+2\sqr3}{2+\sqr3}
On simplifie les dénominateurs
\frac{3-2\sqr3}{2-\sqr3}\times\frac{2+\sqr3}{2+\sqr3}<\frac{2u_n+3}{u_n+2}<\frac{3+2\sqr3}{2+\sqr3}\times\frac{2-\sqr3}{2-\sqr3}

On simplifie en développant numérateurs et dénominateurs, et on obtient
-\sqr{3}<\frac{2u_n+3}{u_n+2}<\sqr3

Et finalement
-\sqr{3}<u_{n+1}<\sqr3

Ca n'a rien à voir avec la croissance de la fonction f()

Posté par
toriore : suite 26-01-09 à 08:57

U(n+1) = f(U(n))

0<= U(n) < rac(3)  (hypothèse)

comme f est croissante (Strictement)

f(0) <= f( (Un) ) < f(rac(3))      et  f(0) = 1,5    f( rac(3) ) = rac(3)

==>

f(0) <= U(n+1) < rac(3)

Posté par
dhaltere : suite 26-01-09 à 15:50

@Torio

Le reproche que je faisais à macene, je te le fais aussi, et c'est d'autant plus grave que tu es celui qui donnes des explications : tu manques de rigueur.

Petite remarque : f n'est pas strictement croissante :
f(-3)=3
f(0)=1.5

Essaie avec cette fonction :
3$g(x)=\frac{x(1.2x-0.2\sqr3-1)}{x-1}
3$g(0)=0 \\ g(\sqr3)=\sqr3
dérivée : je l'ai mise sous une forme qui permet de voir tout de suite que g'(x)>0
3$g'(x)=1.2+0.2\frac{\sqr3-1}{(x-1)^2}

Et pourtant :
si u_n=1.1, alors u_{n+1}=3.52-2.2\sqr3 \approx -0.29 < 0 négative !
si u_n=0.9, alors u_{n+1}=1.8\sqr3-0.72 \approx 2.4>\sqr3

Explication : l'asymptote verticale x=1 est dans l'intervalle [0;\sqr3]
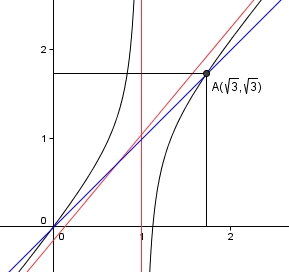
suite
En bleu, la première bissectrice (y=x)
En rouge, les deux asymptotes
Les points O et A sont les points fixes : les éventuelles limites de la suite. Mais la suite ne converge pas nécessairement. Tout dépend de la valeur initiale, et c'est pourquoi j'insistais tellement auprès de macene.

L'étude de la convergence de la suite définie par u_{n+1}=g(u_n) en fonction de la valeur initiale n'est pas triviale.
En particulier, pour u_0=1.1, elle tend vers -\infty, pour u_0=0.9, elle tend vers +\infty

Ta méthode est correcte (à l'imprécision près que je viens de te montrer et dont j'espère que tu la comprendras) à partir du moment où la fonction considérée est définie sur l'intervalle choisi et que l'image de cet intervalle est incluse dans cet intervalle, ça n'a rien à voir avec la croissance de la fonction.
Maintenant, si la fonction est monotone sur cet intervalle, alors la condition : l'image de cet intervalle est incluse dans cet intervalle peut être simplifiée : les images des bornes de la fonction sont dans l'intervalle. C'est cette dernière propriété que tu utilises.

Posté par
toriore : suite 26-01-09 à 19:23

En fait, j'ai montré que :
si 0 <= U(n) < rac(3)  alors  0 <= f( U(n)) < rac(3)   (*)

de la manière suivante :
f(x) = (2x+3)/(x+2) est croissante et continue  dans l'intervalle [0 ; rac(3)[

donc l'image de cet intervalle sera [f(0) ; f(rac(3))[ =  [1,5 ; rac(3)[

ce qui implique que si U(n) se trouve dans [0 ; rac(3)[
alors f( U(n)) se trouvera dans [1,5 ; rac(3)[

ce qui montre (*) me semble-t-il.

Ce qui est vrai, c'est qu'il faut au moins que la première valeur (U(1))
soit dans [0 ; rac(3)[. Détail qui n'était pas précisé dans l'énoncé !

suite

Posté par
macenere : suite 26-01-09 à 19:42

bon soir ce n'est que maintenant que j'ai lue vos reponses en faite pour le premier terme de la suite est U0=0
voila et encore pardon pour mon laxisme et en particulier a toi dhalte

Posté par
toriore : suite 26-01-09 à 19:52

Merci d'avoir précisé U(0).

A+
Torio

Posté par
macenere : suite 26-01-09 à 20:01

c'est en faite ce qui permet de montrer la vérité de ta démonstration torio c'est pour cela que j'ai tenu a le préciser
bon soir

Posté par
dhaltere : suite 26-01-09 à 21:11

Eh bien voilà qui est parfait
@macene : je te demandais cette valeur initiale depuis le début.
@tonio : tu donnes encore une précision supplémentaire, qui manquait à tes messages précédents :

Citation :
et continue

c'est effectivement suffisant.
Lis bien mon message précédent, c'est suffisant mais pas nécessaire.

Voici un exemple de fonction non continue :
\{ x < 1 \; h(x)=1.5x \\ \\ x \ge 1 \; h(x)=1.5(x-\sqr3)+\sqr3
Dont voici le graphe (j'ai ajouté en bleu la première bissectrice)
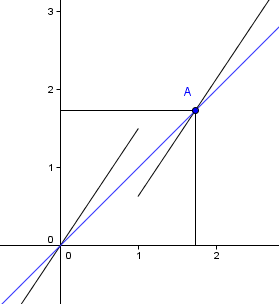
suite
Cette fonction n'est pas continue, mais l'image de l'intervalle [0,\sqr3] est contenue dans cet intervalle.
Aussi, si u_0\in[0;\sqr3], alors pour tout n, on aura u_n\in[0;\sqr3]

Suivant la valeur initiale, est-elle convergente ? Si ça intéresse l'un de vous, posez-vous, posez-moi la question.

En voici une autre, ni continue, ni monotone :
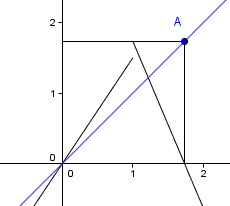
suite
Même propriété de confinement de la suite.

Bonne bourre mathématique à tous


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !