Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

suite récurrente

Posté par
theboss1er 05-09-08 à 21:00

bonsoir

j'ai qq problème pour montrer que : " u(n+1) - u(n) --> l ==> u(n)/n --> l "

je suis parti avec des epsilon mais je n'aboutit à rien d'extraordinaire...

un petit indice serait le bienvenu

merci d'avance

a+

Posté par
gui_toure : suite récurrente 05-09-08 à 21:02

Hello

Indication : utilise la moyenne de Césaro ..

Posté par
perroquetre : suite récurrente 05-09-08 à 21:07

Bonjour, theboss1er

On peut utiliser le théorème de Césaro:   si (v_n) est une suite convergente de limite l, alors 4$ \left(\frac{\sum_{k=0}^{n-1} v_k}{n}\right) converge vers l.

On applique ce théorème à la suite    v_k=u_{k+1}-u_k

Posté par
perroquetre : suite récurrente 05-09-08 à 21:08

Bonjour,  gui_tou  

Posté par
gui_toure : suite récurrente 05-09-08 à 21:09

Bonsoir perroquet

Posté par
theboss1erre : suite récurrente 05-09-08 à 21:10

j'avais émis l'hypothèse de césaro mais je n'avais pas pensé au 'télescopage' merci je vais rédiger

Posté par
theboss1erre : suite récurrente 06-09-08 à 18:44

bonjour
je dois maintenant montrer que 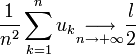suite récurrente
*** image placée sur l'***
j'ai voulu reprendre le principe de la démonstration de la moyenne de césaro mais le fait qu'il y ait n²l au lieu de n*l me gêne....

Posté par
perroquetre : suite récurrente 06-09-08 à 21:37

Le principe est de démontrer que     3$\sum_{k=0}^nu_k-\sum_{k=0}^n kl   est négligeable devant   3$ \sum_{k=0}^n k=\frac{n(n+1)}{2}

Posté par
theboss1erre : suite récurrente 06-09-08 à 22:04

ok merci pour cette indication je vais essayer

a+

Posté par
theboss1erre : suite récurrente 06-09-08 à 23:19

je vois bien que ca donne le résultat mais comment faire pour trouver que c'est ça qu'il faut démontrer ? c'est une astuce ?

à part ca je ne vois pas vraiment comment le prouver..

Posté par
perroquetre : suite récurrente 07-09-08 à 11:30

Soit  \epsilon >0.

\exists N \in {\mathbb N} \quad n\geq N \Longrightarrow \left|\frac{u_k}{k}-l\right|\leq\frac{\epsilon}{2}       donc      3$ n\geq N \Longrightarrow |u_k-kl|\leq k\frac{\epsilon}{2}

On a alors, pour n supérieur à N:
3$ \left|\sum_{k=N}^nu_k-kl\right| \leq \frac{\epsilon}{2} \sum_{k=N}^n k\leq \frac{\epsilon}{2} \sum_{k=0}^nk

N étant fixé, 3$\sum_{k=0}^{N-1}u_k-kl  est une quantité fixe et   3$\sum_{k=0}^nk  est de limite infinie. Il existe donc N' plus grand que N tel que:
3$n\geq N' \Longrightarrow \left|\sum_{k=0}^{N-1}u_k-kl\right| \leq \frac{\epsilon}{2} \sum_{k=0}^n k

On a donc:
3$\forall \epsilon >0 \quad \exists N'\in {\mathbb N}\quad n\geq N' \Longrightarrow \left|\sum_{k=0}^{n}u_k-kl\right| \leq \epsilon \sum_{k=0}^n k

Terminé

Posté par
theboss1erre : suite récurrente 07-09-08 à 12:53

a ouè ok merci beaucoup en tout cas !! donc la je peux dire que la somme des uk - somme des kl est un o(n(n+1)/2)

et un o(n(n+1)/2) en plus l'infini c'est o(n) ?

Posté par
perroquetre : suite récurrente 07-09-08 à 15:00

Citation :

et un o(n(n+1)/2) en plus l'infini c'est o(n) ?


Non, c'est un  o(n^2)

Posté par
theboss1erre : suite récurrente 07-09-08 à 15:03

a ok auriez-vous un moyen de ne pas se tromper quand on est en + l'infini ou en 0 pour savoir quel terme garder en fait ?

je me mélange toujours...

Posté par
perroquetre : suite récurrente 07-09-08 à 15:05

En l'infini, on garde le terme de plus haut degré
En 0, on garde le terme de plus petit degré
(lorsqu'il s'agit de polynômes)

Posté par
theboss1erre : suite récurrente 07-09-08 à 15:15

ok merci bien pour ces réponses

@+


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !