Bonjour ,

Si bien sur que c'est une fonction.
Prends la fonction f(x)=x et g(x)=1 sur l'intervalle [0,2]. Si tu traces son graph ca te donne bien une fonction continue sur [0,2] non ?

Euh, en ce cas, on obtient x[0,1] sup(f,g)(x)=max(f(x),g(x))=a
et
x[1,2] sup(f,g)=f(x)

L'exemple que vous avez donné est en tant qu'un contre exemple à l'idée que j'avais, ou bien le sup est une fonction dans tous les cas puisqu'il varie selon la variation de x.
Il me semble que je n'ai pas encore pigé l'astuce de ton exemple

fais bien les graphes
les deux courbes se croisent en (1,1)
g est dessus avt et après c'est f

Oops,désolée, ce n'est pas "a" mais 1 .
x[0,1] sup(f,g)(x)=max(f(x),g(x))=g(x)=1
x[1,2] sup(f,g)=sup(f)(x)=max(f(x))=f(2)=2
J'ai évité de parler du point du croisement puisqu'on cherche le sup d'un ensemble de fonctions sur un ou plusieurs intervalles.

Non, tu confonds le sup et le max en fait :
Le max(a,b) détermine le plus grand de deux nombres a ou b, alors que le sup(f,g) est définie sur un intervalle et renvoie point par point la valeur maximal des deux fonctions en ce point.

Dans l'exemple que je te donnais, il faut regarder en tout point x de l'intervalle [0,2], lequel de f(x) ou g(x) est le plus grand ce qui donne :
Sur le premier dessin, les graphs de f et g, puis sur le deuxième dessin le sup(f,g).

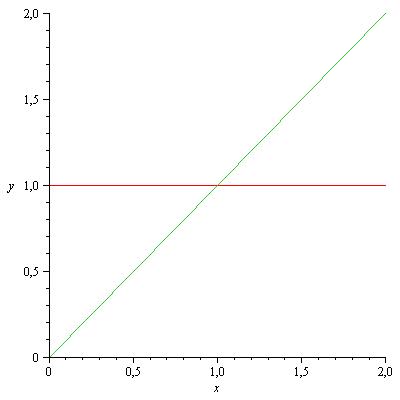
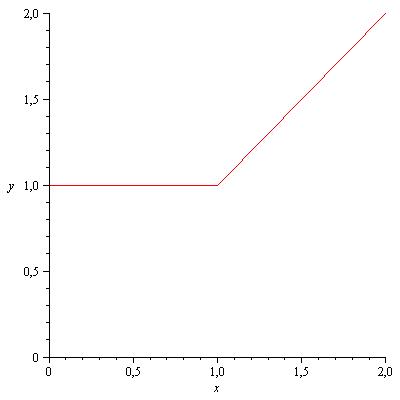
D'après ce que tu as dit, on peut conclure qu'en parlant de max(a,b) on cherche uniquement le plus grand élément de l'ensemble {a,b}.
Mais en écrivant max(f(x)), on désigne la valeur maximale de la fonction f,l'image que peut prendre un certain abscisse "a" appartenant à l'intervalle sur lequel la fonction f est définie.
Aussi, on peut dire que max(f(x))=sup(f)(x) au cas où le sup appartient à Im(f).
Dans l'exemple que tu m'as donnée on a un intervalle fermé [1,2], en particulier du côté de 2. la chose qui m'a donnée sup(f)(x)f([1,2])
  
Non?

max(f(x)) a-t-il un sens ?
Le maximum de deux ou plusieurs nombres est le plus grand de ces nomrbes. C'est aussi un nombre, il n'est pas "défini" sur un ensemble.

Bon, recardons plus précisément sur ce sup. Tu as l'air d'avoir du mal à comprendre ce qu'il représente ( et en comparaison au max ).

Soit f et g deux applications définies sur X. Alors on définit l'appliaction sup(f,g) sur X comme la plus petite fonction supérieur à f et à g.

Salut,

on peut d'ailleurs montrer que , c'est pratique pour montrer la continuité.

Oui voilà, ensuite il faut en venir à cette égalité ( qui se vérifie très facilement ) ce qui assure une continuité.

Merc! Il me semble que j'ai finalement compris!
sup(f,g) est une fonction puisqu'on étudie sa variation sur un intervalle, alors que sup(f,g)(x) est un nombre puisqu'on l'étudie en un abscisse, ainsi on peut dit sup(f,g)(x)=max(f(x),g(x)).
En effet, je confondais entre la borne supérieure d'une fonction f et le sup(f,g).
J'espère que c'est bien ça.
( Sinon, j'espère bien que tu ne t'es pas mis en colère,...)

Et comment démontrer l'égalité que Romu a proposé???

Oui voilà,
Suite à la définition du sup de 2 fonctions, on en déduit que sup est une fonction définie sur le meme ensemble de def de f et g puis que .

Soit tu fais la comparaison avec le max, sinon si tu n'as jamais vu ça et bien lis bien l'égalité.
Il faut montrer qu'en tout point x, sup(f,g)(x)=max(f(x),g(x)) est égale à 1/2(f(x)+g(x)+|f(x)-g(x)|).

Salut,
Voilà, j'ai essayé à démontrer cette égalité,
        max(f(x),g(x))=1/2(f(x)+g(x)+|f(x)-g(x)|)
2.max(f(x),g(x))=f(x)+g(x)+|f(x)-g(x)|
Puisque f et g jouent un rôle symétrique, on suppose que max(f(x),g(x))=f(x)
(afin de maintenir les équivalences).
Donc,
2.max(f(x),g(x))=f(x)+g(x)+|f(x)-g(x)|2.max(f(x),g(x))=2.g(x)max(f(x))=f(x)
Alors que c'est évident !
( La même chose en supposant que max(f(x),g(x))=g(x))
Donc, ce qu'on a supposé est correcte :  max(f(x),g(x))=1/2(f(x)+g(x)+|f(x)-g(x)|)
Est-il correcte en tant qu'une démonstration??

En utilisant l'égalité pour l'exercice, je sais que la somme de deux fonctions continues est une fonction continue, mais est-ce que la valeur absolue de la soustraction ou ( somme / produit / division avec un dénominateur0)sont contninues??

     Bonsoir,

  Hypothèses:
  f:I-R et g:I->R.
  f et g sont continues sur I.
  S:I->R, S(x)=sup(f(x),g(x)).
  
  Nous obtenons: S(x)=(1/2).[f(x)+g(x)+|f(x)-g(x)|].
  f et g sont continues sur I, donc f+g, f-g et g-f sont continues sur I.

  Soient d:I->R,d(x)=f(x)-g(x) et h:I->R, h(x)=|d(x)|.
  d=f-g, donc d est continue. S=f+g+h.
  Nous devons montrer que h est continue sur I.
Soit x0€I
  Pour tout e>0, il existe a>0 tel que:
            x0-a<x<x0+a => d(x0)-e<d(x)<d(x0)+e (1).
  a) Si d(x0)>0, on prend e tel que: 0<e<d(x0). On obtient:
          0<d(x0)-e<d(x)<d(x0)+e.
  Sur ]x0-a;x0+a[, d(x)>0, donc h(x)=d(x), ce qui donne:
            h(x0)-e<h(x)<h(x0)+e.
  b) Si d(x0)<0, on prend e tel que: 0<e<-d(x0).
  On obtient:
           d(x0)-e<d(x)<d(x0)+e<0
           -d(x0)+e>-d(x)>-d(x0)-e>0.
Cette fois ci, h(x0)=-d(x0) et f(x)=-d(x) sur ]x0-a;x0+a[.
            0<h(x0)-e<h(x)<h(x0)+e
c) d(x0)=0, donc h(x0)=0
         x0-a<x<x0+a => -e<d(x)<e , d'où:
         x0-a<x<x0+a => 0<|d(x)|<e
  et sur ]x0-a;x0+a[: 0<h(x)<e,
a), b) et c) montrent que h est continue en tout x0€I.
  Conclusion.
    f, g et h sont continues sur I => Sup(f,g) est continue sur I.
  
    Amicalement.

  
  

"galois"> Merci!!
J'ai fait une autre démonstration , j'espère que tous les passages sont correctes,:
Nous avons f et g deux fonctions continues, donc:
(1)∀ε> 0,∃α> 0,∀x,y ∈ D, |y−x| ≤α ⇒ |f(y)−f(x)| ≤ε/2
et
∀ε> 0,∃α'> 0,∀x,y ∈ D, |y−x| ≤α ⇒ |g(y)−g(x)| ≤ε/2
et puisque |g(y)−g(x)|=|g(x)−g(y)|
(2)∀ε> 0,∃α'> 0,∀x,y ∈ D, |y−x| ≤α' ⇒ |g(x)−g(y)| ≤ε/2
On suppose que α'≤α , donc |y−x| ≤α'≤α ⇒|f(y)−f(x)|+|g(x)−g(y)|≤ε ( en faisant la somme de (1) et (2) )

|y−x|≤α ⇒ |f(y)−f(x)|+|g(x)−g(y)|≤ε , et on sait que |a+b|≤|a|+|b|
      
        ⇒|f(y)−f(x)+g(x)−g(y)|≤ε

        ⇒|(f(y)-g(y))-((f(x)-g(x))|≤ε , et on sait que ||a|-|b||≤|a-b|

|y−x|≤α ⇒||f(y)-g(y)|-|f(x)-g(x)||≤ε

Donc la fonction |f-g| est continue.

C'est correcte?

"Narhm"> Merci, c'est la même idée , mais ta démonstration est beaucoup mieux organisée.

La valeur absolue est-elle continue sur R ? Oui
Si f et g sont continues : f-g est-elle continue ? Oui
La composée de deux fonctions continues est-elle continue ? Oui
La somme de deux fonctions continues est-elle continue ? Oui

Autant se servir des éléments démontrés dans le cours quand c'est fait. Ca évite de tout refaire à chaque fois et ici c'est rapide.

hehehe, je commence à me sentir stupide,...
Sinon, la démonstration que j'ai fait, elle-t-elle correcte??

Oui, ca semble correcte si ce n'est qu'on ne peut pas assurer '<.
Dans ces cas là, on prend =max(',) et on fait tout avec cette nouvelle constante.
Aussi f est continue ssi . Si tu mets les x et y apres les epsilons, alors ta fonction est meme mieux, elle est uniformement continue sur I.

Sinon je pense que tu vois bien que dans un premier temps, tu as montré que si f et g sont continues alors f-g est continue.
Et dans un deuxième temps tu montres que si h est une fonction continue alors |h| est continue.

Bref, maintenant tu as le choix de ta preuve.

PS:Tu peux faire de même avec l'application inf(f,g) ou f et g sont continues sur I.

Merci infiniment!!
Maintenant l'exercice est tellement clair! ^^
Donc sup(f,g) est une "fonction" "continue" sur I !

De rien.

Bonne continuation.

oui et tu peux faire pareil avec .

  Bonsoir,

  Votre démonstration est correcte.
  Cet exercice repose sur la propriété suivante:
        Soit f:I->R;
        Si f est continue alors |f| est continue.
   Si elle a été démontrée en cours, vous l'appliquez à la fonction
    h:I->R, définie par h(x)=f(x)-g(x).
   Sinon vous la démontrez. voici une méthode courte:
   Soit x0€I. La continuité de f en x0 donne:
    pour tout e>0, il existe a>0 tel que:
           |x-a|<a => |f(x)-f(x0)|<e.
    Alors 0<||f(x|-|f(x0)||<=|f(x)-f(x0)|<e, ce qui monter que|f| est continue en x0, puis continue sur I.

  Il semble que cette propriété figure rarement dans les ouvrages.
  Est-elle "officielle"? Je ne le crois pas.

  D'autre part: inf(f,g)=(1/2).[f+g-|f-g|]

   A bientôt.

pour répondre à physics girl il suffit de considérer que

sup(f,g)= (1/2)(f+g-abs(f-g))comme dit ci-dessus.Le procédé est d'ailleurs le même pour montrer que si f et g sont Riemann-intégrables, alors sup(f,g) est Riemann intégrable.