Fiche de mathématiques
Ile mathématiques > maths bac > BAC 2024 TOUJOURS : DES SUJETS VENUS D'AILLEURS
Baccalauréat Mathématiques 2024
Coefficient : 2
Durée : 3 heures
6 points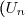) définie par
définie par 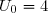 et
et ) .
.
1. Calculer .
.
2. On considère la suite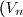) définie par
définie par  .
.
a) Montrer que la suite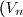) est géométrique en précisant sa raison et son 1er terme.
est géométrique en précisant sa raison et son 1er terme.
b) Donner l'expression de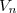 puis celle de
puis celle de 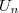 en fonction de
en fonction de 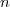 .
.
3. Calculer les limites des deux suites.
4. On pose et
et  .
.
Exprimer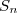 et
et  en fonction de
en fonction de 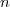 .
.
4 points

1. Représenter le nuage des points de la série statistique) .
.
2. Quel est le prix moyen de l'article entre 2011 et 2018.
3. Calculer l'écart-type du prix de cet article.
10 points définie par
définie par  = 2x^2 - 3 - \ln(x)) .
.
) est la courbe représentative de
est la courbe représentative de  dans un repère orthogonal
dans un repère orthogonal ) avec comme unités graphiques :
5 cm en abscisse et 2 cm en ordonnée.
avec comme unités graphiques :
5 cm en abscisse et 2 cm en ordonnée.
1. Déterminer le domaine de définition de .
.
2. Calculer les limites de aux bornes de son domaine de définition.
aux bornes de son domaine de définition.
3. Justifier que la droite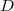 d'équation
d'équation 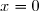 est une asymptote à
est une asymptote à ) .
.
4. Calculer) et donner le sens de variation de
et donner le sens de variation de  .
.
5. Dresser le tableau de variation de .
.
6. Déterminer une équation de la tangente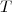 à
à ) au point d'abscisse
au point d'abscisse 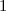 .
.
7. Tracer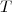 et
et ) .
.
6 points }) définie
par
définie
par  et
et  }) .
.
1. Nous devons calculer .
.

 \\\overset{ { \white{ . } } } { \phantom{ \bullet{\phantom{x}}U_{1}}=\dfrac 12(1+3 \times4) } \\\\\quad\Longrightarrow\quad\boxed{U_1=\dfrac{13}{2}} )

 \\\overset{ { \white{ . } } } { \phantom{ \bullet{\phantom{x}}U_{2}}=\dfrac 12(1+3 \times\dfrac{13}{2}) } \\\\\quad\Longrightarrow\quad\boxed{U_2=\dfrac{41}{4}} )

 \\\overset{ { \phantom{ . } } } { \phantom{ \bullet{\phantom{x}}U_{3}}=\dfrac 12(1+3 \times\dfrac{41}{4}) } \\\\\quad\Longrightarrow\quad\boxed{U_3=\dfrac{127}{8}} )
2. On considère la suite }) définie par
définie par  .
.
2. a) Nous devons montrer que la suite }) est géométrique en précisant sa raison et son 1er terme.
est géométrique en précisant sa raison et son 1er terme.
Pour tout entier naturel ,
,

 } \\\overset{ { \white{ . } } } { \phantom{ V_{n+1}}=1+\dfrac 12+\dfrac 32\, U_n } \\\overset{ { \white{ . } } } { \phantom{ V_{n+1}}=\dfrac 32+\dfrac 32\, U_n } )

 } \\\overset{ { \white{ . } } } { \phantom{ V_{n+1}}=\dfrac 32V_n } \\\\\Longrightarrow\quad\boxed{\forall\,n\in\N, \quad V_{n+1}=\dfrac 32\,V_n} )
Par conséquent, la suite }) est géométrique de raison
est géométrique de raison  et de premier terme
et de premier terme  .
.
2. b) Nous devons donner l'expression de puis celle de
puis celle de  en fonction de
en fonction de  .
.
Le terme général de la suite }) est
est 
Donc, pour tout^n}})
Nous en déduisons que :

^n\end{cases}\quad\Longrightarrow\quad 1+U_n=5\times\left(\dfrac 32\right)^n \\\overset{ { \white{ . } } } { \phantom{\begin{cases}V_n=1+U_n\\V_n=5\times\left(\dfrac 32\right)^n\end{cases}}\quad\Longrightarrow\quad \boxed{U_n=5\times\left(\dfrac 32\right)^n-1}} )
3. Nous devons calculer les limites des deux suites.
D'une part,

^n=+\infty \\\overset{ { \white{ . } } } { \phantom{ \dfrac{3}{2}>1}\quad\Longrightarrow\quad \lim\limits_{n\to+\infty}5\left(\dfrac 32\right)^n=+\infty} \\\overset{ { \white{ . } } } { \phantom{ \dfrac{3}{2}>1}\quad\Longrightarrow\quad \boxed{\lim\limits_{n\to+\infty}V_n=+\infty}} )
D'autre part,

=+\infty \\\overset{ { \white{ . } } } { \phantom{ \lim\limits_{n\to+\infty}V_n=+\infty}\quad\Longrightarrow\quad \boxed{\lim\limits_{n\to+\infty}U_n=+\infty}} )
4. On pose et
et  .
.
Exprimer et
et  en fonction de
en fonction de  .
.
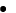
 est la somme de
est la somme de  termes d'une suite géométrique de raison
termes d'une suite géométrique de raison  et de premier terme
et de premier terme  .
.
Dès lors, nous obtenons :

^{n+1}}{1-\dfrac 32} } \\\overset{ { \white{ . } } } { \phantom{ S_n }=5\times\dfrac{1-\left(\dfrac 32\right)^{n+1}}{-\dfrac 12} } } )

![\\\overset{ { \white{ . } } } { \phantom{ S_n }=-10\,\left[1-\left(\dfrac 32\right)^{n+1}\right] } \\\overset{ { \white{ . } } } { \phantom{ S_n }=-10+10\left(\dfrac 32\right)^{n+1} } \\\\\Longrightarrow\quad\boxed{S_n=-10+10\left(\dfrac 32\right)^{n+1} }](https://latex.ilemaths.net/latex-0.tex? \\\overset{ { \white{ . } } } { \phantom{ S_n }=-10\,\left[1-\left(\dfrac 32\right)^{n+1}\right] } \\\overset{ { \white{ . } } } { \phantom{ S_n }=-10+10\left(\dfrac 32\right)^{n+1} } \\\\\Longrightarrow\quad\boxed{S_n=-10+10\left(\dfrac 32\right)^{n+1} } )
De plus,

 + (V_1-1) + \cdots + (V_n-1) \\\overset{ { \white{ . } } } { \phantom{S'_n } =(V_0+V_1+\cdots+V_n)-(1+1+\cdots+1) } \\\overset{ { \white{ . } } } { \phantom{S'_n } =S_n-(n+1) } \\\overset{ { \white{ . } } } { \phantom{S'_n } =-10+10\left(\dfrac 32\right)^{n+1} -n-1 } )

^{n+1} -n } \\\\\Longrightarrow\quad \boxed{S'_n=10\left(\dfrac 32\right)^{n+1} -n-11 } )
4 points

1. Nous devons représenter le nuage des points de la série statistique }) .
.
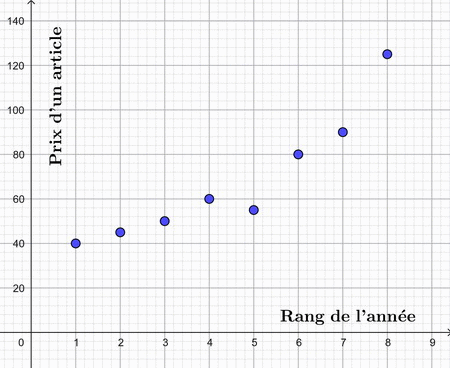
2. Nous devons déterminer quel est le prix moyen de l'article entre 2011 et 2018.
Calculons la moyenne de la variable
de la variable  .
.


Par conséquent, le prix moyen de l'article entre 2011 et 2018 est de 68,125
3. Nous devons calculer l'écart-type du prix de cet article.
du prix de cet article.
Rappelons que^2}{N}} }) .
.
Complétons le tableau mentionnant l'évolution du prix d'un article.
Si nécessaire, les valeurs sont arrondies au millième près.
^2&791,015 &534,765 & 328,515 & 66,015 & 172,265 & 141,015 & 478,515 & 3234,765 \\&&&&&&&&\\ \hline \end{array} })
Nous obtenons ainsi :


10 points définie par
définie par  = 2x^2 - 3 - \ln(x) }) .
.
 }) est la courbe représentative de
est la courbe représentative de  dans un repère orthogonal
dans un repère orthogonal  }) .
.
1. Le domaine de définition de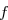 est
est ![\overset{ { \white{ _. } } } {]0\;;\;+\infty[ }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ _. } } } {]0\;;\;+\infty[ }) .
.
2. Nous devons calculer les limites de aux bornes de son domaine de définition.
aux bornes de son domaine de définition.
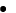 Calculons
Calculons  }) .
.

=-3 \\\lim\limits_{x\to 0^+} \ln(x)=-\infty \end{cases}\quad\Longrightarrow\quad \begin{cases} \lim\limits_{x\to 0^+}(2x^2-3)=-3 \\\lim\limits_{x\to 0^+} -\ln(x)=+\infty \end{cases} \\\overset{ { \white{ . } } } { \phantom{ \begin{cases} \lim\limits_{x\to 0^+}(2x^2-3)=-3 \\\lim\limits_{x\to 0^+} \ln(x)=-\infty \end{cases}}\quad\Longrightarrow\quad \lim\limits_{x\to 0^+}(2x^2-3-\ln(x))=+\infty } \\\overset{ { \white{ . } } } { \phantom{ \begin{cases} \lim\limits_{x\to 0^+}(2x^2-3)=-3 \end{cases}}\quad\Longrightarrow\quad\boxed{ \lim\limits_{x\to 0^+}f(x)=+\infty } } )
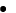 Calculons
Calculons  }) .
.
Pour tout appartenant à
appartenant à ![\overset{ { \white{ . } } } { ]0\;;\;+\infty[ }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ . } } } { ]0\;;\;+\infty[ }) ,
,

=2x^2 - 3 - \ln(x)\quad\Longleftrightarrow f(x)=x^2\left(2-\dfrac {3}{x^2} -\dfrac{\ln(x)}{x^2} \right) \\\overset{ { \white{ . } } } { \phantom{ f(x)=2x^2 - 3 - \ln(x)}\quad\Longleftrightarrow f(x)=x^2\left(2-\dfrac {3}{x^2} -\dfrac 1x\times\dfrac{\ln(x)}{x} \right)} )
Nous obtenons alors :

}{x}=0} \\\text{(croissances comparées)} \end{cases}\quad\Longrightarrow\quad \lim\limits_{x\to +\infty}\left(2-\dfrac {3}{x^2} -\dfrac 1x\times\dfrac{\ln(x)}{x} \right)=2 )
Dès lors,

}{x} \right)=2 }\end{cases}\quad\Longrightarrow\quad \lim\limits_{x\to +\infty}x^2\left(2-\dfrac {3}{x^2} -\dfrac 1x\times\dfrac{\ln(x)}{x} \right)=+\infty \\\overset{ { \white{ . } } } { \phantom{ \begin{cases} \lim\limits_{x\to +\infty}x^2=+\infty\\WWWWWWWWWWWWWW\end{cases}}\quad\Longrightarrow\quad \boxed{\lim\limits_{x\to +\infty}f(x)=+\infty } } )
3. Puisque=+\infty }) , nous en déduisons la droite
, nous en déduisons la droite  d'équation
d'équation  est une asymptote à
est une asymptote à  }) .
.
4. Nous devons calculer }) et donner le sens de variation de
et donner le sens de variation de  .
.
Pour tout appartenant à
appartenant à ![\overset{ { \white{ _. } } } { ]0\;;\;+\infty[ }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ _. } } } { ]0\;;\;+\infty[ }) ,
,

=\Big(2x^2 - 3 - \ln(x)\Big)' \\\overset{ { \white{ . } } } { \phantom{ f'(x)}=4x-0-\dfrac 1x } \\\overset{ { \white{ . } } } { \phantom{ f'(x)}=4x-\dfrac 1x } \\\overset{ { \white{ . } } } { \phantom{ f'(x)}=\dfrac {4x^2-1}{x} } \\\overset{ { \phantom{ . } } } { \phantom{ f'(x)}=\dfrac {(2x+1)(2x-1)}{x} } \\\\\Longrightarrow\quad\boxed{f'(x)=\dfrac {(2x+1)(2x-1)}{x} } )
Déterminons le sens de variation de .
.
Nous observons que pour tout![\overset{ { \white{ _. } } } { x \in\;]0\;;\;+\infty[\;,\quad \begin{cases}f'(x)=\dfrac{2x+1}{x}\times(2x-1)\\2x+1>0\\x>0 \end{cases}\quad\Longrightarrow\quad \dfrac{2x+1}{x}>0 }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ _. } } } { x \in\;]0\;;\;+\infty[\;,\quad \begin{cases}f'(x)=\dfrac{2x+1}{x}\times(2x-1)\\2x+1>0\\x>0 \end{cases}\quad\Longrightarrow\quad \dfrac{2x+1}{x}>0 }) .
.
Dès lors, le signe de }) est le signe de
est le signe de  .
.

&||&-&0&+&\\&||&&&&\\\hline &||&&&&\\f&||&\searrow&&\nearrow&\\&||&&&&\\\hline \end{array} )
Nous en déduisons que :

![\overset{ { \white{ . } } } { \bullet}{\white{x}}\forall\,x\in\;\left]0\;;\;\dfrac 12\right[\;,f'(x)<0 \\\\ \overset{ { \phantom{ . } } } { \bullet}{\phantom{x}}\forall\,x\in\;\left]\dfrac 12\;;\;+\infty\right[\;,f'(x)>0 \\\\ \overset{ { \phantom{ . } } } { \bullet}{\phantom{x}}f'\left(\dfrac 12\right)=0](https://latex.ilemaths.net/latex-0.tex? \overset{ { \white{ . } } } { \bullet}{\white{x}}\forall\,x\in\;\left]0\;;\;\dfrac 12\right[\;,f'(x)<0 \\\\ \overset{ { \phantom{ . } } } { \bullet}{\phantom{x}}\forall\,x\in\;\left]\dfrac 12\;;\;+\infty\right[\;,f'(x)>0 \\\\ \overset{ { \phantom{ . } } } { \bullet}{\phantom{x}}f'\left(\dfrac 12\right)=0 )
D'où, la fonction est décroissante sur l'intervalle
est décroissante sur l'intervalle
![\overset{ { \white{ _. } } } { \left]0\;;\;\dfrac 12\right[ }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ _. } } } { \left]0\;;\;\dfrac 12\right[ }) et est croissante sur l'intervalle
et est croissante sur l'intervalle ![\overset{ { \white{ _. } } } { \left]\dfrac 12\;;\;+\infty\right[ }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ _. } } } { \left]\dfrac 12\;;\;+\infty\right[ }) .
.
5. Nous devons dresser le tableau de variation de .
.

=2\times\dfrac 14-3-\ln\left(\dfrac12\right)\\\phantom{f\left(\frac 12\right)} =\dfrac 12-3+\ln\left(2\right)\phantom{ww}\\\phantom{f\left(\frac 12\right)}=-\dfrac 52+\ln\left(2\right)\phantom{wwW} \\\phantom{f\left(\frac 12\right)}\approx-1,81\phantom{WWWWw}\end{matrix} \begin{matrix} \\||\\||\\||\\||\\||\\||\\||\\||\\||\\|| \\\phantom{WWW}\end{matrix} \begin{array}{|c|ccccc|}\hline &&&&&\\x&0&&\dfrac 12&&+\infty\\ &&&&& \\\hline &||&&&&\\f'(x)&||&-&0&+&\\&||&&&&\\\hline &+\infty&&&&+\infty\\f&||&\searrow&&\nearrow&\\&||&&\ln(2)-2,5\approx-1,8&&\\\hline \end{array} )
6. Nous devons déterminer une équation de la tangente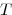 à
à  }) au point d'abscisse
au point d'abscisse  .
.
Une équation de la tangente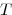 est de la forme :
est de la forme : (x-1)+f(1) }) .
.
=2x^2-3-\ln(x)\\\overset{ { \white{ . } } } { f'(x)=\dfrac {(2x+1)(2x-1)}{x}} \end{cases}\quad\Longrightarrow\quad \begin{cases} f(1)=2-3-\ln(1)\\\overset{ { \white{ . } } } { f'(1)=\dfrac {(2+1)(2-1)}{1}} \end{cases} \\\\\phantom{\text{Or }\quad\begin{cases} f(x)=2x^2-3-\ln(x)\\ { f'(x)=\dfrac {(2x+1)(2x-1)}{x}} \end{cases}}\quad\Longrightarrow\quad \begin{cases} f(1)=-1\\\overset{ { \white{ . } } } { f'(1)=3} \end{cases})
D'où une équation de la tangente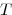 à
à  }) au point d'abscisse
au point d'abscisse  est
est -1 }) , soit
, soit  .
.
7. Nous devons tracer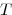 et
et  }) .
.
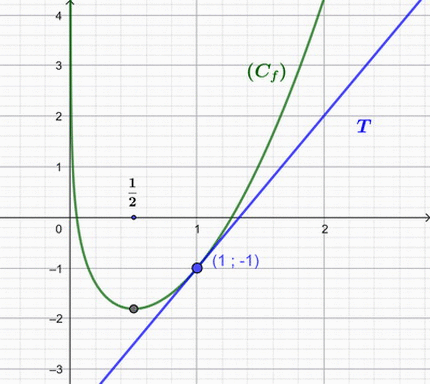
Merci à Hiphigenie et malou pour l'élaboration de cette contribution.
Publié par malou
le
Baccalauréat Mathématiques 2024
Niger séries A4-A8
Durée : 3 heures
6 points
exercice 1
On considère la suite1. Calculer
2. On considère la suite
a) Montrer que la suite
b) Donner l'expression de
3. Calculer les limites des deux suites.
4. On pose
Exprimer
4 points
exercice 2
L'évolution du prix d'un article sur le marché est consigné dans le tableau suivant :1. Représenter le nuage des points de la série statistique
2. Quel est le prix moyen de l'article entre 2011 et 2018.
3. Calculer l'écart-type du prix de cet article.
10 points
probleme
On considère la fonction1. Déterminer le domaine de définition de
2. Calculer les limites de
3. Justifier que la droite
4. Calculer
5. Dresser le tableau de variation de
6. Déterminer une équation de la tangente
7. Tracer
Bac 2024 Niger série A4-A8
6 points
exercice 1
On considère la suite1. Nous devons calculer
2. On considère la suite
2. a) Nous devons montrer que la suite
Pour tout entier naturel
Par conséquent, la suite
2. b) Nous devons donner l'expression de
Le terme général de la suite
Donc, pour tout
Nous en déduisons que :
3. Nous devons calculer les limites des deux suites.
D'une part,
D'autre part,
4. On pose
Exprimer
Dès lors, nous obtenons :
De plus,
4 points
exercice 2
L'évolution du prix d'un article sur le marché est consigné dans le tableau suivant :1. Nous devons représenter le nuage des points de la série statistique

2. Nous devons déterminer quel est le prix moyen de l'article entre 2011 et 2018.
Calculons la moyenne
Par conséquent, le prix moyen de l'article entre 2011 et 2018 est de 68,125
3. Nous devons calculer l'écart-type
Rappelons que
Complétons le tableau mentionnant l'évolution du prix d'un article.
Si nécessaire, les valeurs sont arrondies au millième près.
Nous obtenons ainsi :
10 points
probleme
On considère la fonction1. Le domaine de définition de
2. Nous devons calculer les limites de
Pour tout
Nous obtenons alors :
Dès lors,
3. Puisque
4. Nous devons calculer
Pour tout
Déterminons le sens de variation de
Nous observons que pour tout
Dès lors, le signe de
Nous en déduisons que :
D'où, la fonction
5. Nous devons dresser le tableau de variation de
6. Nous devons déterminer une équation de la tangente
Une équation de la tangente
D'où une équation de la tangente
7. Nous devons tracer

ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter

 Voir la correction
Voir la correction forum de terminale
forum de terminale