Fiche de mathématiques
Ile mathématiques > maths bac > BAC 2024 TOUJOURS : DES SUJETS VENUS D'AILLEURS
Baccalauréat Mathématiques 2024 Côte d'Ivoire
Durée : 2 heures
Coefficient : 2
Toute calculatrice scientifique est autorisée.
2 points
1. et
et  sont des nombres réels.
sont des nombres réels.
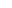 Si
Si ![\lim\limits _ {x\to +\infty}[f(x)-(ax+b)]=0](https://latex.ilemaths.net/latex-0.tex?\lim\limits _ {x\to +\infty}[f(x)-(ax+b)]=0) , alors la droite d'équation
, alors la droite d'équation 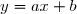 est une
asymptote à la représentation graphique de
est une
asymptote à la représentation graphique de  en
en 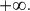
2. Si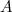 et
et 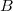 sont deux événements contraires d'un univers
sont deux événements contraires d'un univers 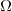 et
et 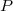 une probabilité sur
une probabilité sur
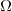 , alors
, alors =1-P(A).)
3. Si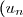_{n\in \textbf N}) est une suite géométrique de premier terme
est une suite géométrique de premier terme 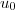 et de raison
et de raison 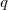 ,
alors
,
alors 
4.=-\infty.)
2 points
5 points) d'inconnue le couple
d'inconnue le couple 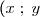) de
de  suivant :
suivant :
\;\left\lbrace\begin{matrix} 3x &+ & y& =&5 \\ x& -& 2y & =& -3 \end{matrix}\right.)
1. Justifier que le couple) est solution du système
est solution du système ) .
.
2. Déduis-en la solution dans du système :
du système :

6 points définie sur
définie sur ![]0\;;\;+\infty[](https://latex.ilemaths.net/latex-0.tex?]0\;;\;+\infty[) par :
par : =5-x+\ln x.)
On note) la représentation graphique de
la représentation graphique de  dans le plan muni d'un repère orthogonal
dans le plan muni d'un repère orthogonal ) d'unités graphiques :
d'unités graphiques : 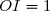 cm et
cm et 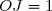 cm.
cm.
1. a. Justifie que :=-\infty.)
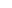 b. Donne une interprétation graphique du résultat précédent.
b. Donne une interprétation graphique du résultat précédent.
2. On suppose que pour tout nombre réel strictement positif,
strictement positif, =x\left(\dfrac 5x -1+\dfrac{\ln x}{x}\right).)
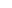 Calcule Calcule
Calcule Calcule . })
3. a. On suppose que est dérivable sur
est dérivable sur ![]0\;;\;+\infty[.](https://latex.ilemaths.net/latex-0.tex?]0\;;\;+\infty[.)
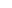 Justifie que pour tout nombre réel
Justifie que pour tout nombre réel  de l'intervalle
de l'intervalle ![]0\;;\;+\infty[\;,\;f'(x)=\dfrac{1-x}{x}](https://latex.ilemaths.net/latex-0.tex?]0\;;\;+\infty[\;,\;f'(x)=\dfrac{1-x}{x}) .
.
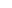 b. Justifie que
b. Justifie que  est croissante sur l'intervalle
est croissante sur l'intervalle ![]0\;;\;1[](https://latex.ilemaths.net/latex-0.tex?]0\;;\;1[) et
décroissante sur
et
décroissante sur ![]1\;;\;+\infty[.](https://latex.ilemaths.net/latex-0.tex?]1\;;\;+\infty[.)
 c. Dresse le tableau de variations de
c. Dresse le tableau de variations de 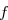 sur l?intervalle de
sur l?intervalle de ![\overset{ { \white{ . } } } {]0\ ;;\ ;+\infty[}](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ . } } } {]0\ ;;\ ;+\infty[})
4. Justifie que l'équation=0) admet une unique solution dans l'intervalle
admet une unique solution dans l'intervalle ![]6,93\;;\;6,94[.](https://latex.ilemaths.net/latex-0.tex?]6,93\;;\;6,94[.)
5 points
Pour cela, le bureau rencontre le proviseur pour connaître les pourcentages des admis au baccalauréat des six dernières années. Les pourcentages sont résumés dans le tableau ci-dessous :

Le président de la promotion soutient que le taux de réussite au BAC de la session 2024 sera d'au moins 90%.
A l'aide d'une production argumentée basée sur les connaissances mathématiques, donne ton avis sur l'affirmation du président.
2 points et
et  sont des nombres réels.
sont des nombres réels.
 Si
Si ![\overset{ { \white{ O. } } } { \lim\limits _ {x\to +\infty}[f(x)-(ax+b)]=0 , }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ O. } } } { \lim\limits _ {x\to +\infty}[f(x)-(ax+b)]=0 , }) alors la droite d'équation
alors la droite d'équation  est une asymptote à la représentation graphique de
est une asymptote à la représentation graphique de 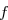 en
en 
Affirmation vraie.
C'est la définition formelle d'une droite asymptote à la courbe représentative d'une fonction.
2. Si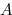 et
et  sont deux événements contraires d'un univers
sont deux événements contraires d'un univers  et
et  une probabilité sur
une probabilité sur  alors
alors =1-P(A). })
Affirmation vraie.
En effet, nous savons que si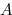 et
et  sont deux événements d'un univers
sont deux événements d'un univers  alors
alors =P(A)+P(B)-P(A\cap B). })
Or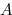 et
et  sont deux événements contraires de l'univers
sont deux événements contraires de l'univers 
Dès lors, soit
soit =1\\ P(A\cap B)=0 \end{matrix}\right. . })
Par conséquent,

=P(A)+P(B)-P(A\cap B)\quad\Longleftrightarrow\quad 1=P(A)+P(B)-0 \\\overset{ { \phantom{ . } } } { \phantom{ P(A\cup B)=P(A)+P(B)-P(A\cap B) } \quad\Longleftrightarrow\quad 1=P(A)+P(B) } \\\overset{ { \phantom{ . } } } { \phantom{ P(A\cup B)=P(A)+P(B)-P(A\cap B) } \quad\Longleftrightarrow\quad \boxed{P(B)=1-P(A) }})
L'affirmation 2 est donc vraie.
3. Si_{n\in \textbf N} }) est une suite géométrique de premier terme
est une suite géométrique de premier terme  et de raison
et de raison  alors
alors 
Affirmation fausse.
L'énoncé correct est le suivant :
 Si
Si _{n\in \textbf N} }) est une suite géométrique de premier terme
est une suite géométrique de premier terme  et de raison
et de raison  alors
alors 
4.=-\infty. })
Affirmation vraie.

![\text{En effet,}\quad\lim\limits_{x\to +\infty}x^2=+\infty\quad\Longrightarrow\quad -\left[\lim\limits_{x\to +\infty}x^2\right]=-\infty \\\overset{ { \phantom{ . } } } { \phantom{\text{En effet,}\quad \lim\limits_{x\to +\infty}x^2=+\infty } \quad\Longrightarrow\quad \boxed{\lim\limits_{x\to +\infty}(-x^2)=-\infty}}](https://latex.ilemaths.net/latex-0.tex?\text{En effet,}\quad\lim\limits_{x\to +\infty}x^2=+\infty\quad\Longrightarrow\quad -\left[\lim\limits_{x\to +\infty}x^2\right]=-\infty \\\overset{ { \phantom{ . } } } { \phantom{\text{En effet,}\quad \lim\limits_{x\to +\infty}x^2=+\infty } \quad\Longrightarrow\quad \boxed{\lim\limits_{x\to +\infty}(-x^2)=-\infty}})
2 points
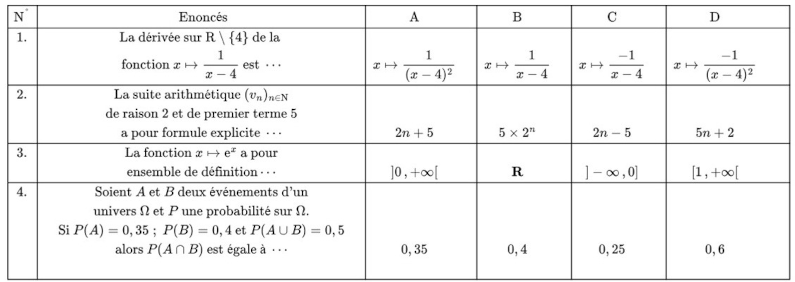
^2} & & x\mapsto \dfrac{1}{x-4} & & x\mapsto \dfrac{-1}{x-4} & & x\mapsto \dfrac{-1}{(x-4)^2} & \\ \hline \end{array})
L'affirmation vraie correspond à la colonne D.
En effet, si=x-4 }) , alors nous obtenons :
, alors nous obtenons :

'=\left(\dfrac{1}{u(x)}\right)' \\\overset{ { \phantom{ . } } } { \phantom{ \left(\dfrac{1}{x-4}\right)'} =\dfrac{-u'(x)}{(u(x))^2}} \\\overset{ { \phantom{ . } } } { \phantom{ \left(\dfrac{1}{x-4}\right)'} =\dfrac{-(x-4)'}{(x-4)^2}} \\\overset{ { \phantom{ . } } } { \phantom{ \left(\dfrac{1}{x-4}\right)'} =\dfrac{-1}{(x-4)^2}} \\\\\Longrightarrow\quad\boxed{\forall\,x\in\R\setminus\lbrace4\rbrace,\quad \left(\dfrac{1}{x-4}\right)'=\dfrac{-1}{(x-4)^2}})
Enoncé n°2
_{n\in \text N}&&&&&&&&&\\&&\text{de raison } 2 \text{ et de premier terme }5&&\phantom{x}2n+5& & \phantom{x}5\times 2^n& & \phantom{x}2n-5& & \phantom{x}5n+2 &\\&&\text{a pour formule explicite }\cdots& && && & & & & \\ \hline \end{array})
L'affirmation vraie correspond à la colonne A.
Rappel : Si) est une suite arithmétique de raison
est une suite arithmétique de raison  dont le premier terme est
dont le premier terme est  alors
alors 
Dans l'énoncé, nous avons : .
.
Dès lors, soit
soit 
Enoncé n°3
![\begin{array} {|c|ccc|cc|cc|cc|cc|} \hline\text N^°&&\text{ Enoncés} & & \text A & & \phantom{xx}\text B & & \text C & & \text D & \\ \hline 3.& & \text{La fonction }x\mapsto \text e ^x\text{ a pour}&&&&&&&&&\\&&\text{ensemble de définition} \cdots & &\phantom{xx}]0\,;+\infty[& & \phantom{xx}\R& & \phantom{xx}]-\infty\,;0]& & \phantom{xx}[1\,;+\infty[ & \\ \hline \end{array}](https://latex.ilemaths.net/latex-0.tex?\begin{array} {|c|ccc|cc|cc|cc|cc|} \hline\text N^°&&\text{ Enoncés} & & \text A & & \phantom{xx}\text B & & \text C & & \text D & \\ \hline 3.& & \text{La fonction }x\mapsto \text e ^x\text{ a pour}&&&&&&&&&\\&&\text{ensemble de définition} \cdots & &\phantom{xx}]0\,;+\infty[& & \phantom{xx}\R& & \phantom{xx}]-\infty\,;0]& & \phantom{xx}[1\,;+\infty[ & \\ \hline \end{array})
L'affirmation vraie correspond à la colonne B.
Enoncé n°4
=0,35\;;\;P(B)=0,4\text{ et }P(A\cup B)=0,5& &\phantom{x}0,35& &\phantom{x}0,4& &\phantom{xx}0,25& &\phantom{xx} 0,6& \\&&\text{alors }P(A\cap B)\text{ est égale à }\cdots &&&&&&&&& \\ \hline \end{array})
L'affirmation vraie correspond à la colonne C.
En effet,

=P(A)+P(B)-P(A\cap B)\quad\Longleftrightarrow\quad0,5=0,35+0,4-P(A\cap B) \\\overset{ { \phantom{ . } } } { \phantom{ P(A\cup B)=P(A)+P(B)-P(A\cap B)} \quad\Longleftrightarrow\quad P(A\cap B)=0,35+0,4-0,5} \\\overset{ { \phantom{ . } } } { \phantom{ P(A\cup B)=P(A)+P(B)-P(A\cap B)} \quad\Longleftrightarrow\quad \boxed{P(A\cap B)=0,25}})
5 points }) d'inconnue le couple
d'inconnue le couple  }) de
de  suivant :
suivant :
\;\left\lbrace\begin{matrix} 3x &+ & y& =&5 \\ x& -& 2y & =& -3 \end{matrix}\right. })
1. Le couple }) est solution du système
est solution du système  })
En effet, si nous remplaçons par 1 et
par 1 et  par 2 dans le système
par 2 dans le système , }) nous obtenons :
nous obtenons :

 }) est bien vérifié par le couple
est bien vérifié par le couple . })
2. Nous devons en déduire la solution dans du système :
du système : 
Posons :
Nous obtenons ainsi :

 \\\\\phantom{\left\lbrace\begin{matrix} 3\text e^x &+ &\text e^y& =&5 \\ \text e^x& -& 2\text e ^y & =& -3 \end{matrix}\right. }\quad\Longleftrightarrow\quad\left\lbrace\begin{matrix} \text e^x & =&1 \\ \text e^y & =& 2 \end{matrix}\right. \\\\\phantom{\left\lbrace\begin{matrix} 3\text e^x &+ &\text e^y& =&5 \\ \text e^x& -& 2\text e ^y & =& -3 \end{matrix}\right. }\quad\Longleftrightarrow\quad\boxed{\left\lbrace\begin{matrix} x & =&0 \\ y & =& \ln 2 \end{matrix}\right. })
Par conséquent, l'ensemble des solutions du système est
est \Big\rbrace}\,. })
6 points définie sur
définie sur ![\overset{ { \white{ . } } } { ]0\;;\;+\infty[ }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ . } } } { ]0\;;\;+\infty[ }) par :
par : =5-x+\ln x. })
1. a) Nous devons justifier que :=-\infty. })
=5\\\overset{ { \white{ . } } } {\lim\limits_{x\to 0}\ln x=-\infty}\end{matrix}\right.\quad\Longrightarrow\quad \lim\limits_{x\to 0}(5-x+\ln x)=-\infty\quad\Longrightarrow\quad \boxed{\lim\limits_{x\to 0}f(x)=-\infty} )
1. b) Interprétation graphique : La courbe }) admet une asymptote verticale d'équation
admet une asymptote verticale d'équation  soit la droite
soit la droite . })
2. On suppose que pour tout nombre réel strictement positif,
strictement positif, =x\left(\dfrac 5x -1+\dfrac{\ln x}{x}\right). })
Nous devons calculer. })
}\end{matrix}\right.\quad\Longrightarrow\quad \lim\limits_{x\to+\infty}\left(\dfrac 5x-1+\dfrac {\ln x}{x}\right)=-1 \\ {\phantom{WWWWWWWWWWWWWWWxWW}}\quad\Longrightarrow\quad \lim\limits_{x\to+\infty}x\left(\dfrac 5x-1+\dfrac {\ln x}{x}\right)=-\infty \\\\ {\white{WWWWWWWWWWWWWWWxWW}}\quad\Longrightarrow\quad \boxed{\lim\limits_{x\to+\infty}f(x)=-\infty})
3. a) On suppose que est dérivable sur
est dérivable sur ![\overset{ { \white{ . } } } { ]0\;;\;+\infty[. }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ . } } } { ]0\;;\;+\infty[. })
Nous devons justifier que pour tout nombre réel de l'intervalle
de l'intervalle ![\overset{ { \white{ . } } } { ]0\;;\;+\infty[\;,\;f'(x)=\dfrac{1-x}{x} . }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ . } } } { ]0\;;\;+\infty[\;,\;f'(x)=\dfrac{1-x}{x} . })
Pour tout nombre réel de l'intervalle
de l'intervalle ![\overset{ { \white{ . } } } { ]0\;;\;+\infty[, }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ . } } } { ]0\;;\;+\infty[, })

=(5-x+\ln x)' \\\overset{ { \phantom{ . } } } { \phantom{ f'(x)} =-1+\dfrac 1x} \\\overset{ { \phantom{ . } } } { \phantom{ f'(x)} =\dfrac {-x}{x}+\dfrac {1}{x}} \\\overset{ { \phantom{ . } } } { \phantom{ f'(x)} =\dfrac {-x+1}{x}} \\\\\Longrightarrow\quad\boxed{\forall\,x>0,\quad f'(x)=\dfrac {1-x}{x}})
3. b) Étudions la croissance de sur l'intervalle
sur l'intervalle ![\overset{ { \white{ . } } } { ]0\;;\;+\infty[. }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ . } } } { ]0\;;\;+\infty[. })
=\frac{1-x}{x} &||&&+&0&-&& \\&||&&&&&&\\\hline &||&&&&&&\\f &||&&\nearrow&&\searrow&& \\&||&&&&&&\\\hline \end{array})
Par conséquent, est croissante sur l'intervalle
est croissante sur l'intervalle ![\overset{ { \white{ . } } } { ]0\;;\;1[ }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ . } } } { ]0\;;\;1[ }) et décroissante sur
et décroissante sur ![\overset{ { \white{ . } } } { ]1\;;\;+\infty[.}](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ . } } } { ]1\;;\;+\infty[.})
3. c) Dressons le tableau de variations de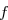 sur l'intervalle
sur l'intervalle ![\overset{ { \white{ . } } } { ]0\;;\;+\infty[. }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ . } } } { ]0\;;\;+\infty[. })
=5-1+\ln 1=5-1+0=4\\\\\\ \begin{array}{|c|ccccccc|}\hline &&&&&&&&x&0&&&1&&&+\infty &&&&&&&& \\\hline &||&&&&&&\\f'(x)&||&&+&0&-&&\\&||&&&&&&\\\hline &||&&&4&&&\\f&||&&\nearrow&&\searrow&&\\&\phantom{XX}||-\infty&&&&&&-\infty\\\hline \end{array})
4. Nous devons justifier que l'équation=0 }) admet une unique solution dans l'intervalle
admet une unique solution dans l'intervalle ![\overset{ { \white{ . } } } { ]6,93\;;\;6,94[. }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ . } } } { ]6,93\;;\;6,94[. })
La fonction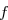 est continue sur l'intervalle
est continue sur l'intervalle ![\overset{ { \white{ . } } } { ]6,93\;;\;6,94[ }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ . } } } { ]6,93\;;\;6,94[ }) car elle est dérivable sur l'intervalle
car elle est dérivable sur l'intervalle ![\overset{ { \white{ . } } } { ]6,93\;;\;6,94[.}](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ . } } } { ]6,93\;;\;6,94[.})
La fonction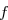 est strictement décroissante sur l'intervalle
est strictement décroissante sur l'intervalle ![\overset{ { \white{ . } } } { ]6,93\;;\;6,94[. }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ . } } } { ]6,93\;;\;6,94[. })
De plus,![\overset{ { \white{ . } } } { \left\lbrace\begin{matrix}f(6,93)\approx0,0059>0\phantom{x}\\f(6,94)\approx-0,0027<0\end{matrix}\right.\quad\Longrightarrow\quad 0\in[f(6,94)\;;f(6,93)] }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ . } } } { \left\lbrace\begin{matrix}f(6,93)\approx0,0059>0\phantom{x}\\f(6,94)\approx-0,0027<0\end{matrix}\right.\quad\Longrightarrow\quad 0\in[f(6,94)\;;f(6,93)] })
Selon le corollaire du théorème des valeurs intermédiaires, nous déduisons l'équation=0 }) admet une unique solution, notée
admet une unique solution, notée  dans l'intervalle
dans l'intervalle ![\overset{ { \white{ . } } } { ]6,93\;;\;6,94[ . }](https://latex.ilemaths.net/latex-0.tex?\overset{ { \white{ . } } } { ]6,93\;;\;6,94[ . })
5 points

Le président de la promotion soutient que le taux de réussite au BAC de la session 2024 sera d'au moins 90%.
Déterminons si le président a tort ou a raison.
Déterminons d'abord s'il y a une bonne corrélation entre les deux variables x et y .
Les moyennes de x et de y sont données par :

Tableau statistique complété.

![\bullet{\phantom{w}}\text{Covariance : }\text{cov}(x;y)=\dfrac{1}{6}\,\sum\limits_{i=1}^6(x_i-\overline{x})(y_i-\overline{y}) \\\\\phantom{ \bullet{\phantom{w}}\text{Covariance : }\text{cov}(x;y)}=\dfrac{1}{6}\,\left[-2,5\times\left(-\dfrac{13}{3}\right)-1,5\times\left(-\dfrac{103}{30}\right)+\cdots+2,5\times\dfrac{287}{30}\right] \\\\\phantom{ \bullet{\phantom{w}}\text{Covariance : }\text{cov}(x;y)}=\dfrac{41,5}{6}=\dfrac{83}{12}](https://latex.ilemaths.net/latex-0.tex?\bullet{\phantom{w}}\text{Covariance : }\text{cov}(x;y)=\dfrac{1}{6}\,\sum\limits_{i=1}^6(x_i-\overline{x})(y_i-\overline{y}) \\\\\phantom{ \bullet{\phantom{w}}\text{Covariance : }\text{cov}(x;y)}=\dfrac{1}{6}\,\left[-2,5\times\left(-\dfrac{13}{3}\right)-1,5\times\left(-\dfrac{103}{30}\right)+\cdots+2,5\times\dfrac{287}{30}\right] \\\\\phantom{ \bullet{\phantom{w}}\text{Covariance : }\text{cov}(x;y)}=\dfrac{41,5}{6}=\dfrac{83}{12})
![\\\\ \bullet{\phantom{w}}\text{Variance : }V(x)=\dfrac{1}{6}\,\sum\limits_{i=1}^6(x_i-\overline{x})^2 \\\\\phantom{ \bullet{\phantom{w}}\text{Variance : }V(x)}=\dfrac{1}{6}\,[(-2,5)^2+(-1,5)^2+\cdots+2,5^2] \\\\\phantom{ \bullet{\phantom{w}}\text{Variance : }V(x)}=\dfrac{17,5}{6}=\dfrac{35}{12} \\\\\phantom{\bullet{\phantom{w}}\text{Variance : }}V(y)=\dfrac{1}{6}\,\sum\limits_{i=1}^6(y_i-\overline{y})^2 \\\\\phantom{ \bullet{\phantom{w}}\text{Variance : }V(y)}=\dfrac{1}{6}\,\left[\left(-\dfrac{13}{3}\right)^2+\left(-\dfrac{103}{30}\right)^2+\cdots+\left(\dfrac{287}{30}\right)^2\right] \\\\\phantom{ \bullet{\phantom{w}}\text{Variance : }V(y)}=\dfrac{9487}{450}](https://latex.ilemaths.net/latex-0.tex?\\\\ \bullet{\phantom{w}}\text{Variance : }V(x)=\dfrac{1}{6}\,\sum\limits_{i=1}^6(x_i-\overline{x})^2 \\\\\phantom{ \bullet{\phantom{w}}\text{Variance : }V(x)}=\dfrac{1}{6}\,[(-2,5)^2+(-1,5)^2+\cdots+2,5^2] \\\\\phantom{ \bullet{\phantom{w}}\text{Variance : }V(x)}=\dfrac{17,5}{6}=\dfrac{35}{12} \\\\\phantom{\bullet{\phantom{w}}\text{Variance : }}V(y)=\dfrac{1}{6}\,\sum\limits_{i=1}^6(y_i-\overline{y})^2 \\\\\phantom{ \bullet{\phantom{w}}\text{Variance : }V(y)}=\dfrac{1}{6}\,\left[\left(-\dfrac{13}{3}\right)^2+\left(-\dfrac{103}{30}\right)^2+\cdots+\left(\dfrac{287}{30}\right)^2\right] \\\\\phantom{ \bullet{\phantom{w}}\text{Variance : }V(y)}=\dfrac{9487}{450})
D'où le coefficient de corrélation est}{\sqrt{V(x)\times V(y)}}=\dfrac{\frac{83}{12}}{\sqrt{\frac{35}{12}\times \frac{9487}{450}}}\approx0,882.})
Puisque les deux variables x et y présentent une bonne corrélation.
les deux variables x et y présentent une bonne corrélation.
Déterminons ensuite par la méthode des moindres carrés une équation de la droite de régression
de régression
de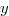 en
en 
Une équation de la droite est de la forme
est de la forme  où
où }{V(x)}}) et
et 
}{V(x)}=\dfrac{\frac{83}{12}}{\frac{35}{12}}=\dfrac{83}{35}\approx2,37\phantom{wwwwwww}\\\\b=\overline{y}-a\overline{x}=\dfrac{498,8}{6}-\dfrac{83}{35}\times3,5=\dfrac{449}{6}\approx74,83\end{matrix}\right.)
Par conséquent, une équation de la droite de régression de
de régression de 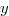 en
en  est :
est : 
Selon ce modèle, donnons une estimation du taux de réussite au BAC de la session 2024.
Le rang de l'année 2024 est 7.
Dans l'équation de , remplaçons
, remplaçons  par 7 et calculons la valeur de
par 7 et calculons la valeur de 

Nous en déduisons qu'une estimation du taux de réussite au BAC de la session 2024 est de 91,43 % , soit un taux supérieur à 90%.
Par conséquent, l'affirmation du président est correcte.
Merci à Hiphigenie et malou pour avoir participé à l'élaboration de cette fiche. Publié par malou
le
Baccalauréat Mathématiques 2024 Côte d'Ivoire
Série A2-H
Coefficient : 2
2 points
exercice 1
Écris le numéro de chaque proposition, suivi de VRAI si la proposition est vraie ou de FAUX si la proposition est fausse.1.
2. Si
3. Si
4.
2 points
exercice 2
Pour chacun des énoncés du tableau ci-dessous, les informations des colonnes A, B, C et D permettent d'obtenir quatre affirmations dont une seule est vraie. Écris le numéro de l'énoncé suivi de la lettre de la colonne qui donne l'affirmation vraie.
5 points
exercice 3
On considère le système d'équations1. Justifier que le couple
2. Déduis-en la solution dans
6 points
exercice 4
On considère la fonctionOn note
1. a. Justifie que :
2. On suppose que pour tout nombre réel
3. a. On suppose que
4. Justifie que l'équation
5 points
exercice 5
Dans le programme d'activités du bureau de la promotion Terminale d'un établissement, est mentionnée : "motivation des candidats pour 100% de réussite au BAC, session 2024".Pour cela, le bureau rencontre le proviseur pour connaître les pourcentages des admis au baccalauréat des six dernières années. Les pourcentages sont résumés dans le tableau ci-dessous :
Le président de la promotion soutient que le taux de réussite au BAC de la session 2024 sera d'au moins 90%.
A l'aide d'une production argumentée basée sur les connaissances mathématiques, donne ton avis sur l'affirmation du président.
Bac Cote d'Ivoire 2024 série A2-H
2 points
exercice 1
1.Affirmation vraie.
C'est la définition formelle d'une droite asymptote à la courbe représentative d'une fonction.
2. Si
Affirmation vraie.
En effet, nous savons que si
Or
Dès lors,
Par conséquent,
L'affirmation 2 est donc vraie.
3. Si
Affirmation fausse.
L'énoncé correct est le suivant :
4.
Affirmation vraie.
2 points
exercice 2
Enoncé n°1L'affirmation vraie correspond à la colonne D.
En effet, si
Enoncé n°2
L'affirmation vraie correspond à la colonne A.
Rappel : Si
Dans l'énoncé, nous avons :
Dès lors,
Enoncé n°3
L'affirmation vraie correspond à la colonne B.
Enoncé n°4
L'affirmation vraie correspond à la colonne C.
En effet,
5 points
exercice 3
On considère le système d'équations1. Le couple
En effet, si nous remplaçons
2. Nous devons en déduire la solution dans
Posons :
Nous obtenons ainsi :
Par conséquent, l'ensemble des solutions du système
6 points
exercice 4
On considère la fonction1. a) Nous devons justifier que :
1. b) Interprétation graphique : La courbe
2. On suppose que pour tout nombre réel
Nous devons calculer
3. a) On suppose que
Nous devons justifier que pour tout nombre réel
Pour tout nombre réel
3. b) Étudions la croissance de
Par conséquent,
3. c) Dressons le tableau de variations de
4. Nous devons justifier que l'équation
La fonction
La fonction
De plus,
Selon le corollaire du théorème des valeurs intermédiaires, nous déduisons l'équation
5 points
exercice 5
Les pourcentages des admis au baccalauréat des six dernières années sont résumés dans le tableau ci-dessous :Le président de la promotion soutient que le taux de réussite au BAC de la session 2024 sera d'au moins 90%.
Déterminons si le président a tort ou a raison.
Déterminons d'abord s'il y a une bonne corrélation entre les deux variables x et y .
Les moyennes de x et de y sont données par :
Tableau statistique complété.
D'où le coefficient de corrélation est
Puisque
Déterminons ensuite par la méthode des moindres carrés une équation de la droite
de
Une équation de la droite
Par conséquent, une équation de la droite
Selon ce modèle, donnons une estimation du taux de réussite au BAC de la session 2024.
Le rang de l'année 2024 est 7.
Dans l'équation de
Nous en déduisons qu'une estimation du taux de réussite au BAC de la session 2024 est de 91,43 % , soit un taux supérieur à 90%.
Par conséquent, l'affirmation du président est correcte.
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter

 Voir la correction
Voir la correction forum de terminale
forum de terminale