Fiche de mathématiques
Ile mathématiques > maths bac > Bac 2020 toujours : des sujets venus d'ailleurs
L'utilisation de la calculatrice non programmable est autorisée.
Le candidat peut traiter les exercices de l'épreuve suivant l'ordre qui lui convient.
L'utilisation de la couleur rouge lors de la rédaction des solutions est à éviter.COEFFICIENT : 7





Publié par malou/relu Panter
le
Bac sciences expérimentales (série SVT et PC) - Maroc 2020
INSTRUCTIONS GENERALES
L'utilisation de la calculatrice non programmable est autorisée.
Le candidat peut traiter les exercices de l'épreuve suivant l'ordre qui lui convient.
L'utilisation de la couleur rouge lors de la rédaction des solutions est à éviter.
COEFFICIENT : 7
DURÉE : 3 HEURES





4 points
On considère la suite définie par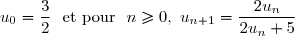
1. On calcule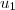 par
par

2. Montrons par récurrence que, pour tout n de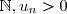
Initialisation: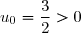 : l'inégalité de l'énoncé est vraie quand n=0
: l'inégalité de l'énoncé est vraie quand n=0
Hérédité: Soit p un entier naturel tel que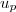 > 0.
> 0.
Alors,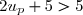 donc 2up+5 est non nul et on peut prendre son inverse,
or l'inverse d'un nombre strictement positif étant strictement positif,
donc 2up+5 est non nul et on peut prendre son inverse,
or l'inverse d'un nombre strictement positif étant strictement positif,
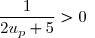 et
et 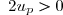 donc en faisant le produit
donc en faisant le produit 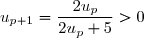
On a montré par récurrence que, pour tout n de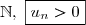
3. a) D'après la question précédente, pour tout n de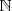 ,
, 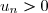 donc
donc 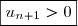 et
et 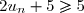 soit
soit
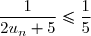 puis
puis 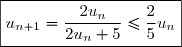
On a donc bien démontré que, pour tout n de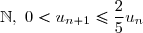
L'inégalité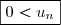 a déjà été démontrée à la question 2.
a déjà été démontrée à la question 2.
Montrons par récurrence que, pour tout n de^n)
initialisation:^0=\dfrac{3}2=u_0) : l'inégalité est donc vraie pour n=0
: l'inégalité est donc vraie pour n=0
hérédité: Soit p un entier naturel tel que^p)
Avec l'inégalité démontrée dans cette même question,
^p = \dfrac{3}2 \left(\dfrac{2}5\right)^{p+1})
On a donc démontré par récurrence que, pour tout n entier naturel,^n})
3. b) Comme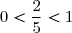 ,
, ^n =0 ) , et à l'aide du théorème des gendarmes, et donc de l'encadrement
, et à l'aide du théorème des gendarmes, et donc de l'encadrement
^n) , vraie pour tout n entier naturel,
, vraie pour tout n entier naturel, 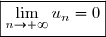
4. On considère à présent la suite définie par, pour tout entier naturel n,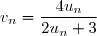
4. a) Exprimons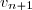 en fonction de
en fonction de 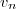
}=\dfrac{8u_n}{10u_n+15}=\dfrac{2}5 \times \dfrac{4u_n}{2u_n+3}= \boxed{\dfrac{2}5 v_n })
On a bien que_{n\in \N) est géométrique de raison
est géométrique de raison 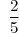
4. b) On en déduit immédiatement que^n\times v_0 \white{o}) avec
avec 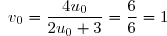
donc pour tout n de^n})
Ensuite, pour tout n de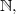
 = 4u_n ~ \iff ~u_n(4-2v_n)=3v_n \quad \left( \text{ on montre facilement que }\left(\dfrac{2}5 \right)^n \neq 2 \right) \\\text{soit encore}~~ u_n= \dfrac{3v_n}{4-2v_n} ~ \iff ~ \boxed{u_n = \dfrac{3 \left(\dfrac{2}5 \right)^n }{4-2 \left(\dfrac{2}5 \right)^n}} )
5 points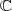 , on considère l'équation (E) :
, on considère l'équation (E) : z+16=0)
1. a) Le discriminant est
\right) ^2 - 4\times 1 \times 16 = -4\left(16-(\sqrt 2 + \sqrt 6\right) ^2)=-4 \left(16-2-2\sqrt{12}-6\right)=-4(8-2\sqrt{12})=-4 \left(6-2\sqrt{12}+2\right)=-4\left(\sqrt{6}^2-2\sqrt{6}\sqrt{2}+\sqrt{2}^2\right))
D'où le résultat^2})
1. b) On a donc deux solutions conjuguées z1 et z2 qu'on détermine par
\right) +i \sqrt{ |\Delta|}}{2\times 1} \text{ et }z_2=\bar{z_1})
ou encore+i\sqrt{4(\sqrt{6}-\sqrt 2)^2}}2 = \dfrac{2(\sqrt 2 + \sqrt 6)+2i(\sqrt{6}-\sqrt 2)}{2}\text{ et } z_2=\bar{z_1} )
donc sont: }z_1=\sqrt{2}+\sqrt 6+i(\sqrt 6 - \sqrt 2) \text{ et } z_2=\sqrt{2}+\sqrt 6-i(\sqrt 6 - \sqrt 2)} )
2. Soient les nombres complexes+i\left(\sqrt 6 - \sqrt 2\right),~~ b = 1+i\sqrt 3 , ~~ c=\sqrt 2 +i\sqrt 2)
2. a) On calcule avec les expressions données :
(\sqrt 2 -i\sqrt 2) = \sqrt 2 -i\sqrt 2 +i \sqrt 2 \sqrt 3 + \sqrt 3 \sqrt 2=\left(\sqrt{2}+\sqrt 6\right)+i\left(\sqrt 6 - \sqrt 2\right) =a)
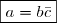
En multipliant cette égalité par , on obtient:
, on obtient: b =4b)
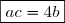
2. b)=\boxed{2\left(\cos\left({\dfrac{\pi}3}\right)+i\sin\left({\dfrac{\pi}3}\right)\right)})
=\boxed{2\left(\cos\left({\dfrac{\pi}4}\right)+i\sin\left({\dfrac{\pi}4}\right)\right)})
2. c) Comme est non nul,
est non nul, 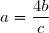 , donc en se servant des formes exponentielles, on obtient:
, donc en se servant des formes exponentielles, on obtient:
}}{2\exp{\left(i\dfrac{\pi}4\right)}}=4\exp\left(i \dfrac{\pi}3-i\dfrac{\pi}4\right)=4e^{i\dfrac{\pi}{12}}=\boxed{4\left(\cos\left({\dfrac{\pi}{12}}\right)+i\sin\left(\dfrac{\pi}{12}\right)\right)})
3. On considère les points B, C et d'affixes respectives b, c et d telle que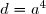 . Soient z l'affixe du point M du plan
. Soient z l'affixe du point M du plan
et z' l'affixe de M' image de M par la rotation R de centre O et d'angle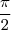
3.a)
Ici,e^{i\dfrac{\pi}{12}} \iff ~ z' = ze^{i\dfrac{\pi}{12}} = \left(\cos\left({\dfrac{\pi}{12}}\right)+i\sin\left(\dfrac{\pi}{12}\right)\right)z \iff \boxed{z'=\dfrac{1}4 az} )
3. b) On applique la formule précédente pour z=c
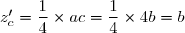
donc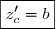
3. c) On a démontré que=b) donc
donc 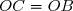 .
.
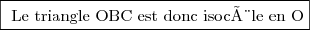
3. d) On a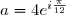
Donc=4^4 \exp \left(i\dfrac{\pi}3\right)=4^4 \left(\dfrac{1}2+i\dfrac{\sqrt 3}2 \right) =4^3\times 2 \times \left(1+i\sqrt 3 \right) = 16 \times 8b ~~ \text{d'où}~~ \boxed{a^4=128b})
Ici,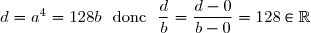 : un de ses arguments est 0, on a bien que
: un de ses arguments est 0, on a bien que  = 0 (\pi))
donc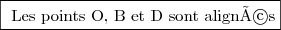 .
.
4 points [ par
[ par =2\sqrt x -2 -\ln(x))
1. a) g est dérivable sur ]0, + [ et pour tout x de ]0, +
[ et pour tout x de ]0, + [,
[, 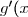=2\times \dfrac{1}{2\sqrt x}-\dfrac{1}{x}=\dfrac{\sqrt x}{ x} - \dfrac{1}x)
Soit![\boxed{\forall x\in ]0,+\infty[\text{ : }g'(x)=\dfrac{\sqrt x -1}{x}}](https://latex.ilemaths.net/latex-0.tex?\boxed{\forall x\in ]0,+\infty[\text{ : }g'(x)=\dfrac{\sqrt x -1}{x}})
1. b) Pour tout de
de 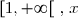 est strictement positif et
est strictement positif et 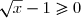
Donc=\dfrac{\sqrt x -1}{x}\geq 0)
D'où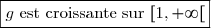
1. c) Puisque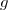 est croissante sur
est croissante sur  \leq g(x))
Donc ) , il s'ensuit que
, il s'ensuit que \leq 2\sqrt{x}-2\leq 2\sqrt{x})
Et comme \geq 0) pour tout
pour tout 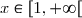
On conclut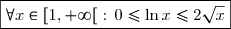
1. d) Notons la fonction définie sur
la fonction définie sur 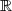 par
par =x^3) .
.
Cette fonction usuelle est croissante sur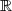 et donc sur
et donc sur 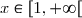 .
.
On a alors:\leq f(\ln x)\leq f(2\sqrt{x}))
On en tire que^3 \leq 2^3 x\sqrt x)
Et comme est non nul, on peut diviser par
est non nul, on peut diviser par 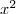
D'où^3}{x^2} \leq \dfrac{8}{\sqrt x}})
Et comme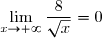
Donc d'après le théorème des gendarmes^3}{x^2}=0 })
2. On considère G:)
2. a) On a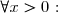
=1 \times \left(-1+\dfrac{4}3 \sqrt x - \ln x \right)+x \times \left(\dfrac{2}{3\sqrt x} - \dfrac{1}x \right)= -1 +\dfrac{4}3\sqrt x -\ln x +\dfrac{2}3 \sqrt x -1 = -2 + \dfrac{6}3 \sqrt x -\ln x =g(x))
Donc![\boxed{G\text{ est bien une primitive de } g \text{ sur } ]0;+\infty[}](https://latex.ilemaths.net/latex-0.tex?\boxed{G\text{ est bien une primitive de } g \text{ sur } ]0;+\infty[} )
2. b) On a
![\begin{aligned}\int_{1}^{4}{g(x)\;\mathrm{d}x\end{aligned}=\left[ G(x)\right]_1^4=4 \left(-1+\dfrac{4}3 \sqrt 4 - \ln 4 \right)- \left( 1\left(-1+\dfrac{4}3 \sqrt 1 - \ln 1 \right) \right)= -4 + \dfrac{32}{3}-4\ln 4 +1 -\dfrac{4}3](https://latex.ilemaths.net/latex-0.tex?\begin{aligned}\int_{1}^{4}{g(x)\;\mathrm{d}x\end{aligned}=\left[ G(x)\right]_1^4=4 \left(-1+\dfrac{4}3 \sqrt 4 - \ln 4 \right)- \left( 1\left(-1+\dfrac{4}3 \sqrt 1 - \ln 1 \right) \right)= -4 + \dfrac{32}{3}-4\ln 4 +1 -\dfrac{4}3)
Or=\ln(2^2)=2\ln(2)) , d'où
, d'où dx}=\dfrac{19}3-8\ln 2})
7 points par
par =-x+\dfrac{5}2-\dfrac{1}2 e^{x-2}\left( e^{x-2}-4\right)) et (C) sa courbe représentative dans un repère orthonormé
et (C) sa courbe représentative dans un repère orthonormé )
1) Lorque x tend vers - , x-2 tend aussi vers -
, x-2 tend aussi vers - et
et =0)
D'où=\lim\limits_{x\to -\infty} -x+\dfrac{5}2 = +\infty})
Lorque x tend vers + , x-2 tend aussi vers +
, x-2 tend aussi vers + et
et =-\infty) ainsi que
ainsi que 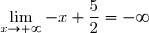
Donc=-\infty})
2. a)
Pour tout x de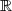 ,
, -\left(-x+\dfrac{5}2\right)=-\dfrac{1}2 e^{x-2}\left( e^{x-2}-4\right))
Et puisque=0)
Alors-\left(-x+\dfrac{5}2\right) = 0) :
:
Ce qui se traduit géométriquement par:
 \text{ d'équation } y=-x+\dfrac{5}{2} \text{ est une asymptote à la courbe } (C) \text{ au voisinage de }-\infty})
2. b) On a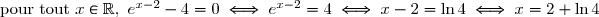
Donc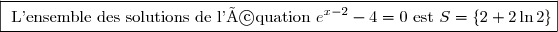
Pour tout réel-\left(-x+\dfrac{5}2\right)= -\dfrac{1}2 e^{x-2}\left( e^{x-2}-4\right) )
Puisque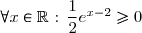 , alors le signe de
, alors le signe de -\left(-x+\dfrac{5}2\right)) est le signe de l'opposé de
est le signe de l'opposé de 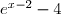
En traçant le tableau de signes:
-(-x+\frac{5}2)&&+&\barre{0}&-&\\\hline\end{tabvar})
On conclut que:
![\boxed{\text{La courbe }(C) \text{ est au-dessus de la droite }(\Delta) \text{ sur } ]-\infty,2+2\ln 2] \text{ et en-dessous de }(\Delta) \text{ sur } [2+2\ln 2 ; +\infty[}](https://latex.ilemaths.net/latex-0.tex? \boxed{\text{La courbe }(C) \text{ est au-dessus de la droite }(\Delta) \text{ sur } ]-\infty,2+2\ln 2] \text{ et en-dessous de }(\Delta) \text{ sur } [2+2\ln 2 ; +\infty[})
3. Pour tout réel non nul, on a:
non nul, on a: }x=-1+\dfrac{5}{2x}-\dfrac{1}{2e^2}\dfrac{e^x}{x}\left(e^{x-2}-4\right))
De plus, on a: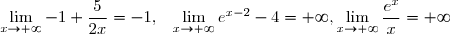
On déduit par opérations élémentaires sur les limites que}x=-\infty})
Interprétation géométrique:\text{ admet l'axe des ordonnées comme direction asymptotique au voisinage de }~+\infty})
4. a) est dérivable sur
est dérivable sur 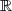 en tant que somme de fonctions dérivables sur
en tant que somme de fonctions dérivables sur 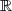 .
.
Donc, pour tout réel :
:
=\left(-x+\dfrac{5}2-\dfrac{1}2 e^{x-2}\left( e^{x-2}-4\right)\right)^{'}=\left(-x+\dfrac{5}2-\dfrac{1}2 e^{2x-4} +2e^{x-2}\right)^{'}=-1-e^{2x-4}+2e^{x-2}=-\left( \left(e^{x-2}\right)^2-2e^{x-2}+1\right))
On a donc bien=-\left( e^{x-2}-1\right)^2})
4. b) Pour tout de
de \leq 0) donc on peut dresser le tableau de variations de
donc on peut dresser le tableau de variations de 
 & &- &\\\hline\niveau{2}{3} f& +\infty& \decroit& -\infty\\\hline\end{tabvar})
5. est deux fois dérivable sur
est deux fois dérivable sur 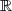 , donc pour tout réel
, donc pour tout réel  , on a :
, on a :
![f''(x)=\left[-\left( e^{x-2}-1\right)^2\right]^{'}=-2(\left( e^{x-2}-1\right)^{'}\left(e^{x-2}-1\right)](https://latex.ilemaths.net/latex-0.tex?f''(x)=\left[-\left( e^{x-2}-1\right)^2\right]^{'}=-2(\left( e^{x-2}-1\right)^{'}\left(e^{x-2}-1\right))
Donc:=-2 e^{x-2} \left(e^{x-2}-1\right)})
Or, on sait que pour tout réel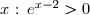 , donc le signe de
, donc le signe de ) est le signe de
est le signe de ) :
:
Et enfin, on a:
On peut tracer le tableau de signes:
 & ~ &+&~ ~&\barre{0}&~~ &- &~ \\\hline\end{tabvar})
On en tire que s'annule en
s'annule en 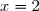 en changeant de signe, donc le point
en changeant de signe, donc le point )) est un point d'inflexion de
est un point d'inflexion de 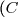)
Or=2)
 \text{ est donc un point d'inflexion de }(C)})
6. D'après le tableau de variations de la question 4.b), est continue et strictement décroissante sur
est continue et strictement décroissante sur 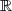
Et comme =+\infty, \lim\limits_{x\to + \infty}f(x)=-\infty ) (question 1)
(question 1)
Donc, d'après le théorème des valeurs intermédiaires , il existe un réel unique tel que
tel que =0) .
.
De plus:
=-2-\ln 3 +\dfrac{5}2 - \dfrac{1}2 e^{2+\ln 3 -2} \left( e^{2+\ln 3 -2}-4\right)= \dfrac{1}2-\ln 3 -\dfrac{1}2 \times 3\times(3-4)=2-\ln 3 > 0)
=\dfrac{1}2-\ln 4 < 0) (d'une manière analogue)
(d'une manière analogue)
On en déduit que: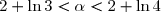
Conclusion:=0 \text{ admet une solution unique }\alpha\text{ telle que } 2+\ln 3 < \alpha < 2+\ln 4})
7.
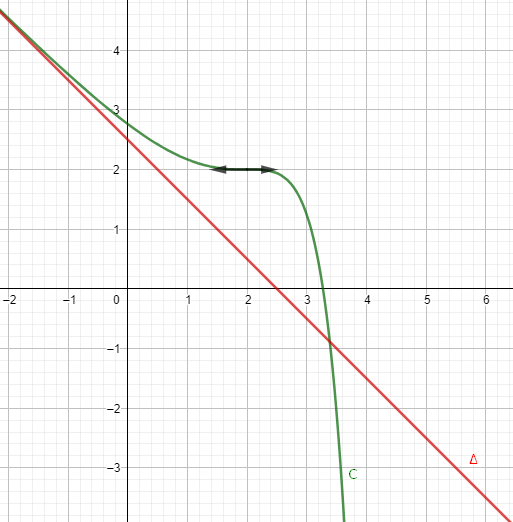
8. a)
Puisque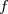 est continue et strictement décroissante sur
est continue et strictement décroissante sur 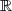 , donc
, donc  est bijective et admet une fonction réciproque
est bijective et admet une fonction réciproque 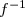 définie sur
définie sur ![f(\mathbb{R})=]\lim\limits_{x\to -\infty} f(x) ;\lim\limits_{x\to +\infty} f(x)[=]-\infty,+\infty[=\R](https://latex.ilemaths.net/latex-0.tex?f(\mathbb{R})=]\lim\limits_{x\to -\infty} f(x) ;\lim\limits_{x\to +\infty} f(x)[=]-\infty,+\infty[=\R )
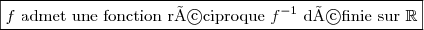
8.b) Pour tracer la courbe de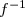 que l'on note
que l'on note ) , il suffit de tracer le symétrique de
, il suffit de tracer le symétrique de 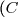) par rapport à la droite d'équation
par rapport à la droite d'équation 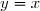 pour obtenir :
pour obtenir :
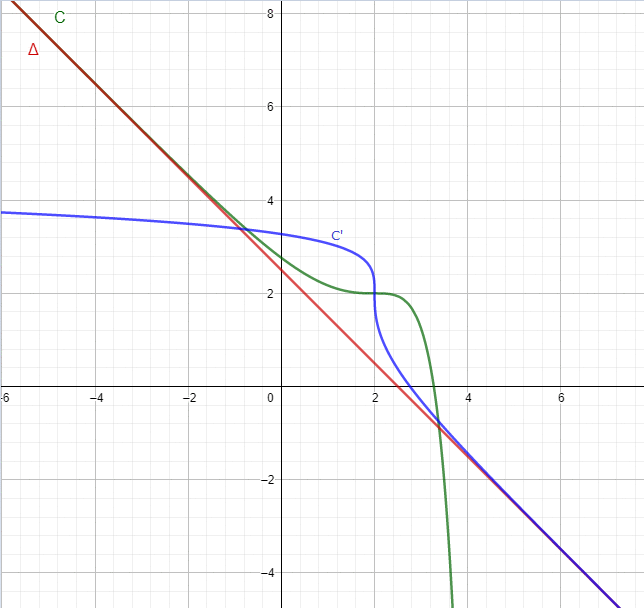
9. Rappel:
Puisque=2-\ln 3) , alors
, alors =2+\ln 3 )
De plus,=-\left(e^{2+\ln 3 -2}-1\right)^2=-4 \neq 0 ) , il s'ensuit que
, il s'ensuit que 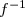 est dérivable en
est dérivable en 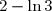 et
et '(2-\ln 3)=\dfrac{1}{f'(2+\ln 3)})
Donc'(2-\ln 3)=-\dfrac{1}4})
exercice 1
On considère la suite définie par
1. On calcule
2. Montrons par récurrence que, pour tout n de
Initialisation:
Hérédité: Soit p un entier naturel tel que
Alors,
On a montré par récurrence que, pour tout n de
3. a) D'après la question précédente, pour tout n de
On a donc bien démontré que, pour tout n de
L'inégalité
Montrons par récurrence que, pour tout n de
initialisation:
hérédité: Soit p un entier naturel tel que
Avec l'inégalité démontrée dans cette même question,
On a donc démontré par récurrence que, pour tout n entier naturel,
3. b) Comme
4. On considère à présent la suite définie par, pour tout entier naturel n,
4. a) Exprimons
On a bien que
4. b) On en déduit immédiatement que
donc pour tout n de
Ensuite, pour tout n de
5 points
exercice 2
Dans l'ensemble des complexes1. a) Le discriminant est
D'où le résultat
1. b) On a donc deux solutions conjuguées z1 et z2 qu'on détermine par
ou encore
donc
2. Soient les nombres complexes
2. a) On calcule avec les expressions données :
En multipliant cette égalité par
2. b)
2. c) Comme
3. On considère les points B, C et d'affixes respectives b, c et d telle que
et z' l'affixe de M' image de M par la rotation R de centre O et d'angle
3.a)
Pour une rotation R de centre P, d'affixe zp, et d'angle 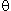 , l'affixe z' de M' image de M d'affixe z par la rotation R est
, l'affixe z' de M' image de M d'affixe z par la rotation R est e^{i\theta})
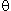 , l'affixe z' de M' image de M d'affixe z par la rotation R est
, l'affixe z' de M' image de M d'affixe z par la rotation R est Ici,
3. b) On applique la formule précédente pour z=c
donc
3. c) On a démontré que
3. d) On a
Donc
Trois points A, B, C d'affixes respectives a, b,et c sont alignés si =\arg\left( \dfrac{c-a}{b-a}\right) = 0 (\pi))
Ici,
donc
4 points
exercice 3
On considère la fonction numérique g définie sur ]0, + [ par
[ par 1. a) g est dérivable sur ]0, +
 [ et pour tout x de ]0, +
[ et pour tout x de ]0, + [,
[, Soit
1. b) Pour tout
Donc
D'où
1. c) Puisque
Donc
Et comme
On conclut
1. d) Notons
Cette fonction usuelle est croissante sur
On a alors:
On en tire que
Et comme
D'où
Et comme
Donc d'après le théorème des gendarmes
2. On considère G:
2. a) On a
Donc
2. b) On a
Or
7 points
probleme
On considère f la fonction numérique définie sur par
par 1) Lorque x tend vers -
 , x-2 tend aussi vers -
, x-2 tend aussi vers - et
et D'où
Lorque x tend vers +
 , x-2 tend aussi vers +
, x-2 tend aussi vers + et
et Donc
2. a)
Pour tout x de
Et puisque
Alors
Ce qui se traduit géométriquement par:
2. b) On a
Donc
Pour tout réel
Puisque
En traçant le tableau de signes:
On conclut que:
3. Pour tout réel
De plus, on a:
On déduit par opérations élémentaires sur les limites que
Interprétation géométrique:
4. a)
Donc, pour tout réel
On a donc bien
4. b) Pour tout
5.
Donc:
Or, on sait que pour tout réel
Et enfin, on a:
On peut tracer le tableau de signes:
On en tire que
Or
6. D'après le tableau de variations de la question 4.b),
Et comme
Donc, d'après le théorème des valeurs intermédiaires , il existe un réel unique
De plus:
On en déduit que:
Conclusion:
7.

8. a)
Puisque
8.b) Pour tracer la courbe de

9. Rappel:
Pour tout point 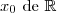 tel que
tel que  \neq 0) ,
, 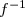 est dérivable en
est dérivable en , ~~\text{et}~~(f^{-1})'(y_0)=\dfrac{1}{f'(x_0)}=\dfrac{1}{(f'of^{-1})(y_0)})
Puisque
De plus,
Donc
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter

 Voir la correction
Voir la correction forum de terminale
forum de terminale