Bonjour,

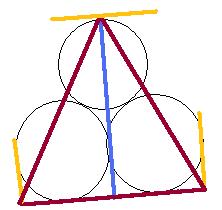
Imagine (ou dessine!) une pyramide de base triangulaire (un triangle équilatéral dont les sommets sont le centre des boules rose, bleue et mauve)
le sommet de la pyramide : le centre de la boule jaune

calcule la hauteur de cette pyramide
et ajoute 2 fois le rayon (au-dessus et en-dessous)

un schéma t'aidera peut-être

Je ne suis pas sur d'avoir compris. Tu veux dire multiplier simplement le diamètre par 2 ? Ce qui ferait 40 cm
Si c'est ce que tu veux dire je pense que non, j'ai fais un dessin (raté) qui montre que ça ne peut pas être 40 cm
La hauteur serait donc 40 - "?"

Si j'ai mal compris ta réponse peut tu me ré expliquer ? merci ^^

Je comprend le schéma que tu m'a donné mais cela revient quand même au final à 40 cm de hauteur.

ton schéma ne correspond pas au mien
Je te parle (cf mon post de 17:01) du centre des boules
en joignant les centres des trois boules du bas, tu obtiens un triangle équilatéral qui se trouve dans un plan "horizontal", au sol à hauteur des 3 centres (donc à hauteur d'un rayon)

la pyramide à imaginer, celle qui est en rouge sur mon schéma, a une hauteur (représentée en vert) qu'il faut calculer
la hauteur serait 40 si ta boule jaune était posée sur la ligne supérieure que tu as tracée

la hauteur à calculer est en vert

Ah ok je pensais que le triangle en question été :

mais ce triangle n'a pas une hauteur de 40 !!

c'est effectivement la hauteur finale à calculer, mais comme ça tu ne peux pas la calculer, il faut prendre les centres pour repères

tu dois calculer AH

Alors c'est un triangle équilatéral, est ce que la méthode pour calculer sa hauteur est la suivante ?

(10 * racine carré de 3) / 2
=(5 * racine carré de 3)
=8.66 cm (environ)

du centre A de la boule du dessus au centre C d'une boule du dessous, donc AC, il y a 2 rayons  (on suppose les boules rigides et qui ne s'aplatissent pas l'une sur l'autre !)
et BC aussi et AB aussi
AH est à la fois hauteur et médiatrice         CH = un rayon

calcule AH par Pythagore dans AHC

AC² = AH² + HC²
20² = AH² + 10²
400 = AH² + 200

AH²= 400 - 200
AH² = 200
AH = 14.14 cm (environ)

Je m'étais bien planté

Et après on multiplie le résultat par 2 ?

Je fais vraiment que des fautes..

AH²= 400 - 100
AH² = 300
AH = 17.32 cm (environ)

Donc après on fait :  17.32 + 20 = 37.32 cm ?

Hallelujah !
Sur ma copie est ce que je dois faire la figure de ton message de 19h27 ?
Merci de ton aide et te ta patiente surtout

oui, ou celui-là
ou mieux celui de 17:49 qui est plus explicite de la démarche, en rajoutant les lettres au besoin

de rien

C'est re moi ^^
J'ai demandé à mon professeur si cette méthode été bonne il m'a répondus que ce n'était pas exactement le bon résultat en faisant en fonction de la figure de 19:27.
Est ce qu'il y a une autre formule pour calculer la hauteur d'une pyramide triangulaire dont les côté valent tous 20 cm, c'est à dire en fonction du schéma de 17:49 ?
Merci

oui, je te refais le schéma de 17:49 avec des lettres
j'avoue avoir laissé passer ton résultat erroné de AH ( mon dessin de 19:27 était destiné à te faire comprendre que la hauteur n'était pas 40 cm.)

Voilà

BDC est un triangle équilatéral (imagine-le horizontal)
AH : la hauteur du centre A de la boule jaune au plan du triangle BDC
H est équidistant de B, D et C (c'est ce qui nous intéresse : intersection des médiatrices),
mais H est aussi intersection des médianes (et hauteurs) en violet du triangle équilatéral BDC
Or les médianes se coupent au tiers de leur longueur en partant du milieu d'un coté --> HI = 1/3 BI

Calcul de BI :
Pythagore dans BID rectangle en I (avec ID = 1/2 DC)

Calcul de AH :
Pythagore dans AHI rectangle en H  (avec HI = 1/3 BI)

n'oublie pas de rajouter les 2 rayons : celui de A au haut de la boule jaune et celui du plan du triangle BDC (et donc de H) au bas des autres boules

dis-moi ce que tu trouves

Ok alors,

BD² = BI² + ID²
20² = BI² + 10 ²
400 = BI² + 100

BI² = 400 - 100
BI² = 300
BI = 17.32

BI = AI = 17.32
HI = 17.32 / 3 = 5.77

AI² = AH² + HI ²
17.32² = AH² + 5.77²
299.98 = AH² + 33.29

AH² = 299.98 - 33.29
AH² = 266.69
AH = 16.33

La hauteur est égale à 16.33+20 = 36.33cm   alors qu'avec l'autre méthode elle est de 37.32 cm
Je pense que c'est bon mais je ne sais pas comment le présenter sur ma copie :/

je pense aussi que c'est bon, pour la démarche en tous cas c'est ça (je n'ai pas refait les calculs à la calculette!)

refais ce dessin (le dernier avec les lettres)
précise que A,B,C,D : centre des boules
que AB = BC = CD = DB = 2  fois le rayon =....
et puis reprends mon post de 14:53 en n'oubliant pas de préciser Pythagore ... dans le triangle ... rectangle en ....  et en intercalant tes calculs

Encore merci pour ton aide