Inscription / Connexion Nouveau Sujet
Aide maths, niveau 2nde, triangles semblables
On mène aux extrémités A et B du segment AB les perpendiculaires Ax et By d´un même coté de AB.
Soit C un point de AB, on porte sur Ax et By deux segments variables AM et BN tels que
AM.BN=AC.CB
En gros la figure ressemble a ca
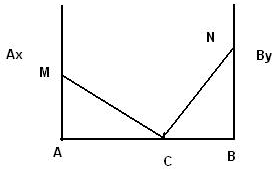
1)Comparer les triangles MAC et CBN
2)Quelle est la valeur de l´angle MCN, et quelle ligne est décrite par le centre du cercle CMN?
3)Soit CP la hauteur issue de C du triangle MCN, Comparer APB et MCN
Montrer que le point P décrit un demi cercle de diamètre AB
Voila c´est niveau seconde, mais je lutte vraiment
pour la 1) je dirai qu´ils sont semblables mais je ne sais pas pourquoi
2)90° mais j´ignore la raison
3) Je seche . . .. Surement montrer que P=90° avec un diamètre [AB] mais peu sur
Merci davance !
Pour une lisibilité directe, j'ai attachée l'image ^^
Après avoir + réfléchi,
1)Semblables car la relation est donnée (mais c'est très tiré par les cheveux)
2)MCN=90° mais la démonstration je l'ignore toujours
La ligne décrite est le diamètre je crois
3)Comme ils sont semblables(la démonstration me fait défaut), on aura P=90° donc ca décrit un demi cercle
Merci(encore) de me corriger, voire m'aider a trouver ce que j'ignore


SVP j'ai vraiment besoin de votre aide
Derniere tentative, je vous en prie aidez moi ^^
Bonsoir Tequila!
Je donne un petit nom aux longueurs de ton image comme suit:
x1=AC, x2=CB, y1=AM et y2=BN.
La donnée nous dit que . Comme C est fixé, x1 et x2 le sont aussi. Si je fixe M (et donc y1) N est automatiquement fixé et
. Les triangles MAC et CBN sont rectangles. Je compare maintenant le rapport de leur catètes:
Et là tu as la justification que ces triangles sont semblables. Les angles bleus sur mon dessin sont donc égaux, de même que les angles rouges. Comme l'angle bleu + l'angle rouhe donne 90 (somme des angles dans le triangle rectangle), si tu fais le bilan des angles en C tu verras que MCN ne peut être que 90.
J'espère t'avoir donné des idées.
 Isis
Isis




