Inscription / Connexion Nouveau Sujet
Aire d un demi-cercle et Théorème de Bijection.
Bonjour, j'ai commencé un exercice, mais je me trouves bloqué à la Question 1°b). Pourriez-vous m'aider, me donner des pistes ?
Voici l'exercice :
On considère le demi-cercle C de diamètre [AB], de centre O et de rayon 1 représenté ci dessous.
On veut placer, avec une bonne précision, un point M sur ce demi-cercle de façon que la droite (AM) partage le demi-disque limité par [AB] et C en deux surfaces de même aire.
Puisque je n'peux pas représenter le schéma :
- M est situé sur l'arc de cercle en 
/4.
(Si vous pouvez m'aider ou si vous allez tenter, vaut mieux faire un petit croquis de la situation).
On note 
la mesure en radians de l'angle BÔM, étant comprise entre 0 et .
1°a) Quelle est l'aire du demi-disque limité par [AB] et C ?
Calculer l'aire A1() du triangle AOM et l'aire A2() du secteur circulaire BÔM.
1°b)En déduire que l'aire A() de la partie du demi-disque située sous la droite (AM) est égale à :
1/2 ( + sin )
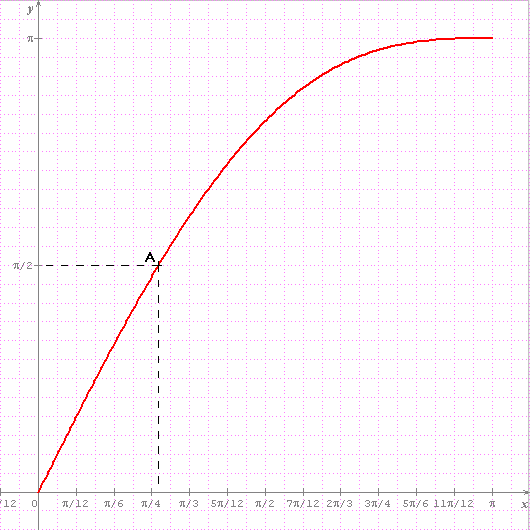
2°. Soit f la fonction : x 
x + sin x.
2°a) Dresser le tableau de variations de f sur [0 ; ].
2°b) Démontrer qu'il existe un réel 0 et un seul de [0 ; ] tel que :
f(0) = /2
A l'aide de la calculatrice, donner une valeur approchée de 0 et de sin 0 à 10-2 près.
3°. Conclure.
On considère le demi-cercle C de diamètre [AB], de centre O et de rayon 1 représenté ci dessous.
On veut placer, avec une bonne précision, un point M sur ce demi-cercle de façon que la droite (AM) partage le demi-disque limité par [AB] et C en deux surfaces de même aire.
Puisque je n'peux pas représenter le schéma :
- M est situé sur l'arc de cercle en pi/4.
(Si vous pouvez m'aider ou si vous allez tenter, vaut mieux faire un petit croquis de la situation).
On note a la mesure en radians de l'angle BÔM, a étant comprise entre 0 et pi .
1°a) Quelle est l'aire du demi-disque limité par [AB] et C ?
Calculer l'aire A1(a) du triangle AOM et l'aire A2(a) du secteur circulaire BÔM.
1a)pir²/2=pi/2
Si A est bien à gauche avec H projeté de M sur AB
A1(a) = AHM - OHM = (1+cosa)(sina)/2 - cosa.sina/2 = (sina)/2
A2(a)=(a/2).r²=a/2
d'où A(a)=A1+A2=(a+sina)/2
Vérifies
Philoux
oups
désolé Nicolas
Philoux
>tu devrais trouver ceci avec un alpha_zéro = 0,83 radian (48° env)
soit un petit peu plus des 45° de ton dessin 
Salut Nicolas
Philoux
En 1°a), Aire du demi-disque : /2 
R².
Puisqu'ici R = 1, L'aire du demi disque est de /2 ?
AOM est un riangle isocèle, mais je ne me souviens plus de la formule pour calculer l'aire d'un triangle quelconque ? (Ll)/2 ?
Après, d'après la somme des angles d'un triangle égale à , je trouves que AÔM = (3)/2
Puisqu'on a AO = OM = 1, ... Je n'arrives plus à poursuivre pour trouver l'aire.
Quant à BÔM, Aire = /2 R²
Soit l'Aire de BÔM = (/4)/2 1²
= /8 ?
Sinon, pour la suite, qu'est ce que H ?
Annuler
connectez vous