Inscription / Connexion Nouveau Sujet
aire sous la courbe
Voila l'exercice:
Les deux première question on va dire que je sais l'expliquer! mais je ne comprend pas et je ne vois pas comment on peut faire pour la question 3. Pouvez vous m'aider? merci d'avance!
Le but de l'exercice est d'établir dans un cas particulier le lien existant entre aire sous la courbe et primitive. On prendra comme requis la définition suivante : H est une primitive de h sur [a ;b] si et seulement si H est dérivable sur [a ;b] et si pour tout x de [a ;b] on a H'(x)=h(x)
Dans la suite, on note f la fonction définie sur |R par f(t)=ln(t²+1)
1.Expliquer pourquoi f est continue sur [0 ; + l'infini[.
2.Montrer que f est croissante sur [0 ; + l'infini[
Pour £>ou=0, on note A(£) l'aire de la portion de plan limitée par l'axe des abscisses, la courbe représentative de f et la droite d'équation x=£.
J'ai en anexe le dessin de la courbe
3.a. Soit les réels x0>0 et h>0. En utilisant un rectangle convenablement choisi, établir l'encadrement :
ln(1+x0²)<ou= [A(x0+h)-A(x0)]/h<ou=ln[1+(x0+h)²]
b. Quel encadrement peut on obtenir de la même manière pour h<0 et h>ou=-x0 ?
c. Démontrer que A est dérivable en xo. Quel est le nombre dérivé de A en xo?
4.Expliquer pourquoi ln(2)<ou=A(2)<ou=2ln(5)
ABCD -> 3.75 unité d'aire soit 3.75 cm²
ABEF -> 4.25 cm²
mais c'est une aproximation
enfait c deux aire encadre l'air qu'on cherche non?
sur mon dessin j'ai comme unité 1=5 petits careaux.
on cherche l'encadrement de A(x0+h)-a(x0)/h mais je ne comprend pas bien d'ou elle sort... elle illustre l'air de ABED?
mais ou va t'on cherche les ln?
Il fallait prendre x0 et non pas 4 comme abscisse du point A.
Dans ces conditions :
A(x0, 0)
B(x0+h, 0)
C(x0+h, f(x0)) ou bien C(x0+h, ln(x02+1))
D(x0, f(x0)) ou bien D(x0, ln(x02+1))
E(x0+h, f(x0+h)) ou bien ...
F(x0, f(x0+h)) ou bien ...
Il faut alors dire que :
Aire(ABCD) < < Aire(ABEF)
je cherche je cherche!
mais pour les aires des deux rectangle il fo que je fasse aussi l'integrale? je vais voir je vais me pancher sur ma feuille et je reviens
nan j'ai rien dis!!! comme c'est un rectangle japplique la formule!!!
mais puis je dire que:
xo+h xo f(x).dx = A(xo+h)-A(xo)
comment le prouver?
Non,
L'aire du rectangle ABCD est égale à AB
BC=hf(x0))=hln(1+x02)
Celle du rectangle ABEF est égale à ABBE=hf(x0+h))=hln(1+(x0+h)2)
Enfin l'aire comprise entre la courbe et l'axe Ox est égale à : .
Il suffit alors d'écrire les choses ...
oui oui pour les rectangle c ce que j'ai fait.
Mais je vois pas comment on peux passer de l'integrale a A(xo+h)-A(xo) pour avoir la formule du centre de l'inequation.
ensuite je divise par h ...
Oups, le coup est parti tout seul !
Je voulais dire
Sur les figures ci-dessous, on voit ce que représente A(x0+h) puis A(x0)...
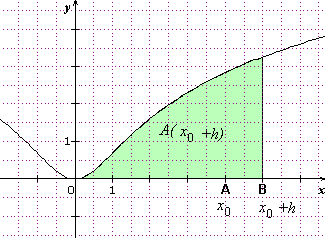
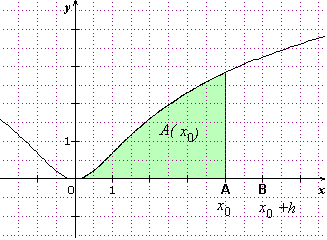
oui d'accord c'est par definition!! d'accord!! le dessin sont bien explicite!! merci!!
j'ai continue l'exercice.
Pour la question b quand h est strictement negatif lorsque l'on divise par h qui est neg cela change les signe nous avons donc:
ln(1+xo²)
A(xo+h)-Axo/hln(1+(xo+h)²)
je pense...
mais h-xo je ne la comprend pas trop...
Annuler
connectez vous