Inscription / Connexion Nouveau Sujet
Algorithme
Bonjour,
Soient A, B et H trois points non alignés.
Ecrire un algorithme permettant de construire le point C tel que H soit l'orthocentre du triangle ABC.
Quelqu'un aurait-il une idée ?
Tu es bien en seconde ?
intersection de :
- la droite passant par A et de vecteur directeur le vecteur normal à (BH)
- la droite passant par B et de vecteur directeur le vecteur normal à (AH)
Oui j'ai fais une figure, l'orthocentre c'est le point d'intersection des hauteurs d'un triangle, une hauteur étant une droite passant par un sommet et qui est perpandiculaire au coté opposé à ce sommet
si "une hauteur étant une droite passant par un sommet et qui est perpendiculaire au coté opposé à ce sommet"
alors :
- la droite passant par A et de vecteur directeur  à BH
à BH
est la droite du coté AC;
- la droite passant par B et de vecteur directeur  à AH
à AH
est la droite du coté BC;
et l'intersection des deux donne le point C.
Essaye de visualiser sur la figure.
j'ai commencer à ecrire un algorithme dites moi si ça peut etre bon ou pas :
placer les points a b et h non alignés
tracer le segment [BA]
tracer une droite (AH)
tracer une droite (BH)
puis tracer une droite (HC) perpendiculaire au segment [BH]
vecteur directeur = vecteur qui donne la direction de la droite.
Mais peut-être ne connais-tu que le terme de coefficient directeur.
Méprise de ma part, peut-être..
On te demande un algorithme de construction géométrique
et non un algorithme de résolution numérique ? c'est ça ?
Si c'est le cas, on va faire autrement.
je ne connais aucun de ces deux termes à vrai dire 
Mais avec l'explication que vous m'avez donné je vois ce que sait. Aucune méprise de votre part !!
Oui c'est un bien algorithme de construction
Dans ce cas :
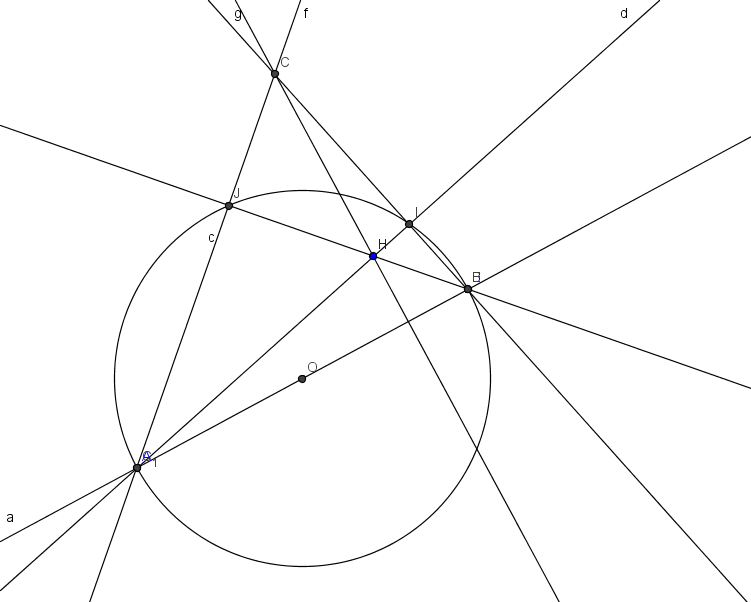
(1) - construire la droite passant par H  (AB)
(AB)
(2) - construire le cercle de diamètre [AB]
(3) - construire la droite (AH);
elle coupe le cercle (2) en I;
puis construire la droite (BI)
(4) - construire la droite (BH);
elle coupe le cercle (2) en J;
puis construire la droite (AJ)
(5) - le point C est obtenu comme l'intersection de deux des
trois droites construites en (1), (3) et (4)
Merci beaucoup , mais le probleme c'est que votre algorithme ne répond pas à la consigne car là ça fait triangle ABH avec C orthocentre alors qu'il faut que ça soit triangle ABC avec H comme orhocentre :s
non, non. pas du tout.
on cherche bien le sommet C du triangle ABC tel que H soit l'orthcentre.
suit l'algorithme et fais les constructions indiquées.
J'ai suivis toutes les étapes et à la fin l'intersection de deux des trois droites construites me donnent H 
les consignes sont bonnes.
l'intersection de (BI) et de (AJ) ne peut pas donner
le point H; elle donne bien le point C.
en (5), je te réécris différemment la consigne :
(5) - le point C est obtenu comme l'intersection de
(BI), de (AJ) et de la droite construite en (1)