Bonjour, fais un dessin (je t'ai fait un exemple avec n = 5 puis n = 10) :

geogebra donne les sommes dans les deux cas, ça permettra de vérifier si l'algorithme calcule bien.

Avant de faire un algorithme il faut que tu trouves comment tu calculerais ces deux aires à la main (et avec n rectangles, pas 5 ou 10 )?

Bonjour,

pour joindre une figure lire et appliquer la FAQ (bouton "?" en haut)
vu que la figure tu l'as, ça nous éviterait d'en refaire une (fastidieux de dessiner 2n rectangles)

l'aire des rectangles :

quelle est leur largeur ? (en fonction de n)
ils ont un sommet sur la courbe
quelle est son abscisses ? comment varie cette abscisse x en fonction du numéro du rectangle ?
quelle est son ordonnée (facile c'est f(x) !)
et donc quelle est son aire ?

l'algorithme découle directement de ces considérations

initialiser S = 0
pour chaque valeur de x abscisse d'un coin
calculer l'aire du rectangle correspondant
ajouter cette aire à S
passer à la valeur de x suivante

faire pareil pour les rectangles inférieurs et pour les rectangles supérieurs (mais c'est pas les même coins !)
pour calculer deux sommes : Sinf la somme des rectangles inférieurs
Ssup la somme des rectangle supérieurs

afficher à la fin : l'aire est comprise entre Sinf et Ssup

à détailler pour en faire un algorithme prêt à être codé.

bonjour Glapion, je n'avais pa svu ton message
le roi des séquences sur Geogébra

Bonjour Glapion merci beaucoup de m'aider!

Mais comment je peux calculer l'aire rouge par example, sachant que je ne connais pas le nombre de rectangle ?

Bonjour mathafou, tu lui a expliqué de façon très pédagogique comment structurer cet algorithme.
on va voir s'il trouve les formules qui donnent les aires des n ième rectangles (d'habitude, ils ont toujours un peu de mal à concrétiser des formules justes, surtout en seconde)

edenrose, le nombre de rectangles, tu le laisses égal à n. il sera demandé au début de l'algorithme, c'est une variable, peu importe que l'on ne connaisse pas sa valeur, il faut écrire des formules qui marchent pour tout n.

Mais il faut que tu cherches un peu :
A quelle abscisse commence le n ième rectangle ?
Quel est sa largeur ? quelle est sa longueur ?

la largeur d'un rectangle serai
1/ n
Mais la longeur se serai quoi ducoup ?

j' ai essayer de répondre aux question que vous m'avez posé x étant le numéraux du rectangle
la largeur serai : (1/n)x
l' abscisse du dernier rectangle serai 1 on le calculerai comme cela (1/n)x
en revanche je bloque sur la longueur et l'ordonné, comme c'est une fonction carré j'ai pensé faire : racine carré de(1/n)x
mais je ne suis pas dutout sure de moi

ne pas confondre x une abscisse
et le numéro du rectangle !
ni le nombre de rectangles

la largeur sera : (1/n)x
non 1/n fois la largeur totale (qui est 1 ici, qui sera 2 à la question 3b)
donc la largeur de chaque rectangle est 1/n

1er rectangle supérieur : quel coin de ce rectangle est sur la courbe ?
quelle est son abscisse (de ce coin) ?
quelle est son ordonnée (il est sur la courbe !!)
et donc quelle est la hauteur de ce rectangle
et donc son aire

2ème rectangle supérieur : mêmes questions
3ème rectangle supérieur : "" ""
...
rectangle supérieur de numéro k : mêmes questions
...
dernier rectangle supérieur : "" ""


faire pareil avec les rectangles inférieurs.

ducoup d'après ce que j'ai compris l'algo donnerais inferieur

Etrée:  S, l, Longueur, x et n sont des variables

Traitement : s=0
                           l= (1/n)x
                            Longueur = 0
     pour x allant de 1 à n
                  s= ( ( l*Longueur)n)

sortie:  afficher s

ahh je viens de comprendre mon erreur je vais réessayer

avant d'écrire un algo il faut déterminer les formules qui seront utilisées dans l'algo !!
erreur classique de débutant : se précipiter sur l'écriture de l'algo (voire sur son clavier de calculette pour taper directement un programme) avant d'avoir étudié formellement le problème.

l'algo c'est à la fin
pas au début.

1er rectangle supérieur :
le coin de ce rectangle sur la courbe est le coin supérieur droit
l'abscisse de ce point est (1/n)1
l'ordonné  c'est f((1/n)1)
la hauteur est égale à l'ordonné donc c'est f((1/n)1)
et l'aire c'est (1/n)*((1/n)1)

rectangle k
le coin supérieur droit est sur la courbe
l'abscisse es (1/n)k
l'ordonné f((1/n)k)
hauteur f((1/n)k)
aire (1/n)*((1/n)k)

dernier rectangle
le coin suérieur droit est sur la courbe
abscisse est 1
ordonné 1
hauteur1
aire 1

presque

et l'aire c'est (1/n)*((1/n)1)
bein non !!!
l'aire c'ets largeur*hauteur
et la hauteur c'est f((1/n)1) (tu l'as écrit sur la ligne juste au sdessus !!)

donc l'aire c'est (1/n)*f((1/n)1)
pareil pour tous

et en plus : le dernier est doublement faux car sa largeur est aussi 1/n

es que ce que j'ai écris c'est juste ?

ce que tu as écrit est faux (c'est bien ce que j'ai dit, j'ai écrit "non" et "faux")
et je t'ai montré où étaient tes erreurs.

ENTREE: ssup, sinf,x ,l, h, n  sont du type nombre

TRAITEMENT:
ssup prend la valeur 0
sinf prend la valeur 0
l prend la valeur 1/n
h prend la valeur f((1/n)x)

Pour x allant de 1 à n
ssup =((1/n)*f((1/n)x))x
sinf= ((1/n)*f((1/n)x))x
Fin Pour

SORTIE: Afficher ssup
                     Afficher sinf

es que sa c'est juste du cou ?

PS: je sais que je ne l'ai pas écrit de manière conventionnelle

h prend la valeur f((1/n)x) ne sert à rien du tout (d'ailleurs nulle part tu n'utilies h dans la suite)

ssup =((1/n)*f((1/n)x))x

faux pour de multiples raisons :

- c'est quoi ce "x" qui traine à la fin ??

- on veut faire la somme des rectangles

pour cela on remplace l'ancienne valeur de cette somme (ssup, initialisée au départ à 0)
par la somme de cette ancienne valeur et de l'aire de ce rectangle qui est juste (1/n)*f((1/n)x)

sinf= ((1/n)*f((1/n)x))x
est faux pour une raison supplémentaire :
il est évident que à la fin tu obtiendrais la même chose que ssup !!
c'est visiblement faux

tu n'as pas pris en compte que le coin qui est sur la courbe n'est pas le même que celui pour les rectangles supérieurs
son abscisse n'est donc pas (1/n)x
et sa hauteur par conséquent pas f((1/n)x))

ENTREE: ssup, sinf,x ,l, h, n  sont du type nombre

TRAITEMENT:
ssup prend la valeur 0
sinf prend la valeur 0
l prend la valeur 1/n  

Pour x allant de 1 à n
h prend la valeur f((1/n)x)
ssup =((1/n)*(h)) +x((1/n)*(h))

SORTIE: Afficher ssup
                     Afficher sinf

c'est mieux comme sa ? en revanche je n'ai pas compris ce que je devais mettre pour  sinf , désoler si je suis longue à la détente mais j'essaye de comprendre vos commentaire et de les prendres en compte mais  pour moi les algo c'est vraiment très compliqué donc je suis vraiment désoler si je vous fait rabaché les choses

pour que tu compennes bien ce que l'on doit faire vraiment, je te rajoute une variable

variables: ssup, sinf,x ,l, h, n, rectsup sont du type nombre

TRAITEMENT:
ssup prend la valeur 0
sinf prend la valeur 0
l prend la valeur 1/n

Pour x allant de 1 à n
h prend la valeur f((1/n)x)
rectsup = h*l // aire de ce rectangle
ssup = ssup + rectsup // je cumule ce rectangle avec l'aire totale en cours de calcul dans ssup

évidemment cette variable est inutile si on écrit directement :

ssup = ssup + l*h (lettre l)

h elle même est inutile si on écrit directement :

ssup = ssup + l*f(l*x) (lettres l pas des chiffres 1)

ah bein oui 1/n (chiffre 1) c'est l (lettre l), inutile de le recalculer à chaque fois !

ça c'était pour ce que tu avais déja écrit concernant ssup

passons à sinf

reprends les schémas de Glapion :
je te dessine juste un rectangle sup et un rectangle inf, tous deux de même rang (rang que tu as appelé x, choix malheureux de nom mais passons)



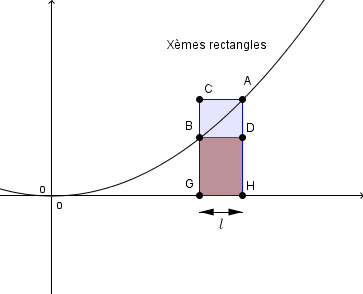
tu as calculé l'aire du Xème rectangle "sup" ACGH en calculant sa hauteur AH
le point A ayant pour abscisse l*x et pour ordonnée AH = f(l*x) (lettres l)

maintenant on veut calculer l'aire du rectangle inf (rouge) DBGH
le coin de ce rectangle qui est sur la courbe est B
quelle est son abscisse ?
son ordonnée ? et donc la hauteur BG de ce rectangle et son aire

Merci beaucoup mathafou , maintenant j'ai bien compris comment calculer l'aire des rectangles supérieurs ;P
Je pense que le rectangle DBGH a comme:
abscisse (1/n)x
Ordonnées f((1/n)x-1) ce qui donne aussi la hauteur puisse qu'ils sont égaux
par conséqant l'air serai :
h*l ce qui en toute écriture donne
f((1/n)x-1) * (1/n)

et en algo sa donnerai
TRAITEMENT ssup= 0
                                  sinf=0
                                  l=1/n
Pour x allant de 1 à n

h prend la valeur f((1/n)x-1)
rectsinf = h*l
sinf = sinf + rectsinf

pour le rectangle inférieur, l'abscisse de B n'est pas (1/n)x mais c'est "le point d'avant" donc (1/n)(x-1)
(chiffre 1)
parenthèses obligatoires

Ordonnées f((1/n)(x-1)) tout à fait mais parenthèses obligatoires (remarque précédente)

on peut écrire aussi l'abscisse de B comme (1/n)x - l (lettre l) vu que en développant (1/n)(x-1) = (1/n)x - 1/n et que 1/n = l

le reste me semble bon si on corrige cette absence de parenthèses obligatoires (ou certains chiffres 1 en lettres l)

il ne reste plus qu'à écrire le plus proprement possible l'algorithme complet en entier (les deux calculs d'un coup)

D'accord je vais faire sa meri beaucoup mathafou

citation inutile.
il suffisait de citer b) et c)

quand la question a) sera réellement terminée :

pareil pour b) sauf que la fonction f(x) n'est pas la même et les bornes pas les mêmes.

un programme général permettrait des paramètres variables :
la valeur de départ de l'abscisse a (au lieu de 0, c'est ça qu'il faut changer)
la valeur d'arrivée b (au lieu de 1, et ça)
le nombre n de rectangles
la fonction f (dans Algobox, la fonction f serait définie dans l'onglet "utiliser une fonction numérique")

pour la question c on "remarque" que la courbe de la question b) est un demi-cercle de rayon 1
et donc l'aire devrait être /2
la valeur approchée obtenue par la question b est donc une valeur approchée de /2, d'où la question c
il faut choisir le nombre de rectangles (n) pour avoir la précision demandée.
(et prouver que c'est un demi-cercle)

Bonjour je n'ai pas compris pourquoi dans le b)  je devais remplacer la valeur de départ de l'abscisse par a et la valeur d'arrivé par b

le but de mettre des variables au lieu de constantes "en dur" pour les bornes est de rendre le programme plus général

dans la question a) c'est pour l'abscisse de 0 à 1
dans la question b) c'est pour l'abscisse de -1 à 1 (mais en vrai de -1 à 0 voir plus loin)

ces valeurs interviennent à plusieurs endroit (le "0" de 0 à 1 intervient réellement plusieurs fois)

donc tant qu'à faire noter de façon absolument générale ces bornes sur l'abscisse comme étant [a; b] explicitement dans deux variables a et b initialisées
dans la question a) comme a = 0, b = 1
dans la question b) comme a = -1, b = 0

je ne vais pas discuter plus avant sur le choix des noms de variables mais pour rendre le programme plus clair et lisible je renomme
l (confusion avec le chiffre 1) en d
et x en k (un rang est un nombre entier, alors que x est plutôt réservé pour une abscisse, un nombre réel)

le programme "général" devient alors :

entrées ou paramètres :
n = 10 (pour 10 rectangles par exemple)
a = 0 (pour la question a)
b = 1
fonction f(x)
traitement :
d = (b-a)/n // largeur d'un rectangle = largeur totale b-a divisée par le nombre n de rectangles
Sinf = 0
Ssup = 0
pour k de 1 à n
Ssup = Ssup + d*f(a+d*k)
Sinf = Sinf + d*f(a+d*(k-1))
fin pour
afficher Sinf "< S <" Ssup

il y a alors vraiment très peu de modifications à faire pour que ce programme qui marche exactement aussi bien (et est plus lisible) pour la question a)
et soit réutilisable presque sans modification pour les questions b) et c)

en fait en analysant plus finement ce qu'il se passe réellement comme différence entre la question a) (bornes de 0 à 1)
et la question b) (bornes de -1 à +1) on remarquerait un piège bien méchant :

il ne faut pas faire la somme de -1 à +1 pour la question b) !!!
mais de -1 à 0 et multiplier le résultat par 2

parce que notre méthode de calcul pour identifier quel rectangle est "inférieur" et quel rectangle est "supérieur" nécessite que la fonction soit croissante sur tout l'intervalle considéré

or dans la question b) la fonction est croissante dans [-1; 0] et décroissante dans [0; 1] !!
faire la somme sur l'intervalle [-1; 1] donnerait un résultat faux. (les deux sortes de rectangle étant inversées dans la deuxième partie de l'intervalle, dans [0, 1])

on peut s'assurer éventuellement, par un message d'avertissement ou par un test explicite dans le programme, que l'utilisateur ne donne pas des âneries en guise de données, en imposant b > a et que la fonction soit définie et croissante pour tout x de [a; b]
on ne va pas se lancer dans une telle complication ici, c'est à l'utilisateur de faire gaffe.

la question b) se borne donc à modifier
la définition de la fonction f
les bornes a = -1 et b = 0 au lieu de a = 0 et b = 1
à multiplier le résultat par 2 (le deux moitiés identiques de l'intervalle)
sans toucher au "coeur" de l'algorithme.

et la question c) est identique à la question b) en multipliant par 4 au lieu de 2 le résultat.

D'accord merci, juste la nouvelle fonction c'est quoi du coup ?

Je veux dire comment elle s'écrit dans l'algo du b)

Une autre question quand tu dis multiplié par 2 le résultat, c'est multiplier le résultat de ssup et sinf c'est sa ?

c'est écrit dans l'énoncé :

a) la fonction c'est f(x) = x²
question b) f(x) = racine(1-x²)
question c) : la même (racine(1-x²) : "en déduire", mais il faut le justifier)

un algorithme c'est une simple écriture de la suite des opérations (mathématiques et logiques), de leur enchainement.
écrire f(x)=racine(1-x²) ou ou n'importe quelle façon "mathématique" d'écrire ça.

ne pas confondre avec la traduction d'un algorithme en un programme
dans un langage déterminé, pour une machine déterminée

ça ne s'écrira pas pareil selon qu'on écrit ça :
en C
sur Algobox
sur calculette de chez TI
sur calculette de chez Casio
sur Scratch (c'est à la mode en collège "ça")
etc

il ne me semble pas avoir lu dans l'énoncé de consignes pour imposer de faire ça sur une machine particulière ...
on peut donc le faire aussi bien sur une calculette, ou sur Algobox, ou en Python etc etc
et "les détails" de traduction ne seront pas écrits pareil.


"le résultat" c'est le couple de deux valeurs Ssup et Sinf
donc oui, multiplier par 2 c'est multiplier par 2 Ssup et multiplier par 2 Sinf. (tout à la fin, une fois le calcul fait)
parce que chaque rectangle est une fois à gauche et le même à droite par symétrie,
donc la somme de tous les rectangles "inf" c'est deux fois la somme de tous les rectangles inf de gauche seulement
et pareil pour les rectangles "sup"
on ne calcule que la moitié de l'aire : la moitié de gauche, puis à la fin on multiplie tout par 2