- Arithmétique dans Z - supérieur
- Exercice : le petit théorème de Fermat
- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Licence Maths 1e ann ArithmétiqueTopics traitant de arithmétique [tout]Lister tous les topics de mathématiques
Niveau Licence Maths 1e ann
algorithme d'euclide étendu
Posté par help123
Bonsoir,
J'aimerai comprendre les détails du calcul pour trouver l'inverse de 79 modulo 3220, surtout pour la colonne A
En effet j'ai une correction qui me présente ceci sous forme de tableau :
Merci
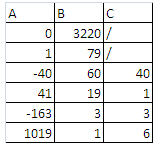
Et comme ça, tu comprends mieux?
| Qn | Rn | Un | Vn |
| 3220 | 1 | 0 | |
| 79 | 0 | 1 | |
| 40 | 60 | 1 | -40 |
| 1 | 19 | -1 | 41 |
| 3 | 3 | 4 | -163 |
| 6 | 1 | -25 | 1019 |
avec
Bonjour,
Toujours sur le sujet de la cryptographie en utilisant le système RSA, j'ai compris les valeurs de la colonne A et B. En revanche pour la colonne C je ne comprends pas comment on trouve la valeur 2842 et les suivantes.
Merci d'avance !
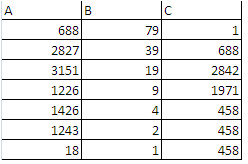



 arithmétique en post-bac
arithmétique en post-bac