Inscription / Connexion Nouveau Sujet
Algorithme de dichotomie
Bonjour.
Voila j'ai un exercise à rendre pour mardi 13 octobre. Voici mon problème:
F est une fonction définie sur un intervelle [a;b] représentée ci-contre. On suppose que l'équation f(x)=0 admet une solution unique x0 dans l'intervalle [a;b]. On considère l'algorithme suivant:
Entrées
Saisir
a,b:bornes de l'intervalle de définition
f:fonction étudiée
N:entier naturel, N 1
1
Traitement
Pour k de 1 jusqu'à N
m prend la valeur a+b
2
Si f(m) et f(a) sont de même signe alors
a prend la valeur m
sinon
b prend la valeur m
FinSi
FinPour
Sorties
Afficher a,b
a)On applique cet algorithme à la fonction f définie sur l'intervalle [0;1] par f(x)=x3+2x-2. Prendre N=4 et compléter le tableau suivant:
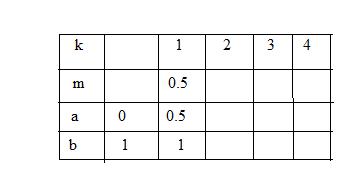
b)Quel est le rôle de cet algorithme? Expliquer en particulier la fonction de la variable N.
c)Traduire cet algorithme dans un language de programmation et tester le programme obtenu.
Merci de votre aide. Au revoir
Edit Coll : forum modifié ; élève de seconde
Bonjour,
Lorsque k=2 :
m prend la valeur (a+b)/2=(0,5+1)/2=0,75
f(m)=-0,08 environ et f(a)=-0,88 donc f(m) et f(a) sont de même signe
donc a prend la valeur 0,75 et b reste inchangé (b garde la valeur 1)
Lorsque k=3 :
m prend la valeur (a+b)/2=(0,75+1)/2=0,875
f(m)=0,42 environ et f(a)=-0,08 donc f(m) et f(a) ne sont pas de même signe
donc a reste inchangé (a garde la valeur 0,75) et b prend la valeur de m, c'est à dire 0,875
Lorsque k=4 ...
bonjour à tous
mon fils a un dm a faire et je suis incapable de lui expliquer
j ai bien compris le systeme pour remplir le tableau
mais je ne comprends pas bien a quoi cet cet algorithme que represente k et à quoi sert n
si je dois faire une representation graphique de la fonction quelle fonction doit-on prendre?
merci de m aider çà fais 25 ans qu j etais en seconde
Bonjour,
que represente k et à quoi sert n
k est une variable entière qui sert de compteur de boucles dans la structure "pour k de 1 jusqu'à n"
La valeur de k ne sert à rien d'autre qu'à compter le nombre d'itération au fur et à mesure du déroulement de l'algorithme.
n est aussi un entier et permet à l'utilisateur de choisir le nombre de boucles à faire (et donc d'augmenter la précision des calculs).
re bonjour
merci de cette precision mais c est bien ce que j avais deduis
pour le représentation graphique dois-je prendre
f(x)=x3+2x-2
merci de me donner cette precision
Bonjour à tous,
j'ai le même exercice sachant que j'ai bien compris l'exrcice je beug avec la caculatrice !
pouvez vous me donner le programme de lA TI82 SVPP
Je vous remercie d'avance...
Bonjour,
Merci pour le lien je beug toujours un peu savez vous comment traduire "de même signe" avec la calculatrive SVP
J'ai a rendre ce devoir pour le vendredi qui vient
et j'ai du mal pour la question b : Quel est le rôle de cet algorithme? Expliquer en particulier la fonction de la variable N.
Pouvez vous m'aider svp !
Bonjours a tous & a toutes.
J'ai un DM de Mathématique a rendre pour DEMAIN ! '--
Et je ne comprend toujours pas ma maniere de proceder dans le tableau...
Je n'arrive pas non plus à expliquer avec mes propres mots ce qu'est un Algorithme de Dichotomie & quel est le rôle particulier de N.
Voici ma fonction et le tableau que je dois remplir : f(x)= 3x²-2x-2 .
K _?_ 1 2 3 4
M _?_ ...
A 1 _?_ ...
B 2 _?_ ...
Aidez moi au plus vite SVP 
 (((
(((
bonjour,
je cherche a installer le programme de dichotomie sur ma calculatrice ti 83 plus mais je ne le trouve
pas !
pouvez vous m'aider?
merci
bonjour,
je cherche a installer le programme de dichotomie sur ma calculatrice ti 83 plus mais je ne le trouve
pas !
pouvez vous m'aider?
merci
Bonjour 
cet algorithme est tjs d'actualité
le rôle de la variable N: voir réponse de P. Rabiller du 01.11.09 à 12.39
rôle de l'algoritmme : donner un encadrement de x pour lequel f(x)=0; x  [a;b]?
[a;b]?


