- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
Algorithme linéarisation d'une courbe
Bonjour,
Pouvez-vous me donner une piste pour me lancer dans la résolution de ce problème, je n'arrive vraiment pas à me lancer...
Voici l'énoncé : Proposer un algorithme qui permet de linéariser une courbe dans le but d'améliorer la précision d'une capteur de mesure X. On recherche l'ordonnée MesLinX pour toute mesure (MesX).
Principe : On relève les diverses coordonnées des points de la courbe, extrémités de 11 segments de droite. On note dans un tableau TabX les xi et dans un autre TabY les yi, qui permettront de calculer les coefficients ai et bi caractérisant le segment ( Y=aX+b ).
Image énonce ici : 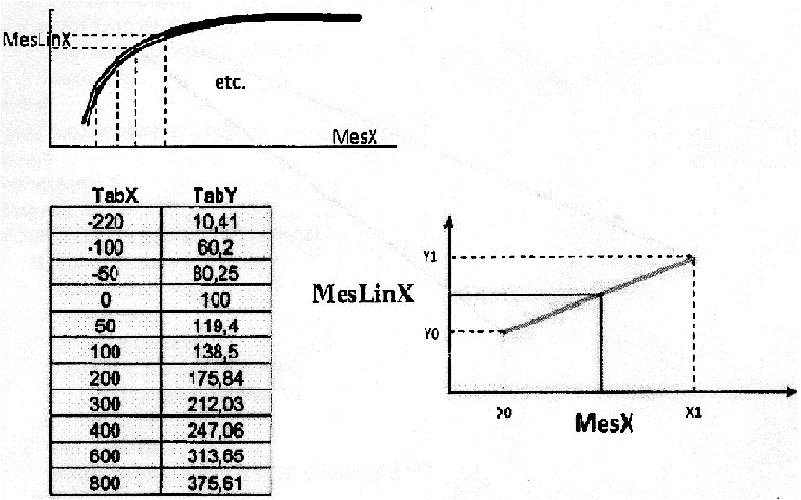
* Tom_Pascal > image placée sur le serveur de l' , merci d'en faire autant la prochaine fois Francoise... *
, merci d'en faire autant la prochaine fois Francoise... *
Je vous remercie par avance pour votre aide.
Cordialement.
Tu écris un programme comportant une boucle
i parcourant indice_début ... indice_fin
a reçoit (y(i+1) - y(i))/(x(i+1) - x(i))
b reçoit y(i) - ax(i)
MesLink(i) reçoit a*MesX(i) + b
Bonjour,
Déjà merci pour votre réponse.
Cependant,vu mon niveau assez faible en algo je ne comprends vraiment pas votre raisonnement, pourriez-vous développer svp?
Je vous remercie par avance,
Cordialement,
On parcourt le tableau que tu as reproduis.
A chaque étape, on considère deux lignes successives du tableau: il faut une origine et une extrémité pour calculer le segement.
On commence par les deux premières lignes, puis on prendra la deuxième et la troisième, puis la troisième et la quatrième, ...
L'extrémité du segment qu'on vient de calculer devient l'origine du segment suivant.
A l'intérieur de la boucle:
- on calcule le coefficient directeur a du segment (formule de math)
- on calcule la constante b de l'équation y = ax + b de la droite qui porte le segment
- MesX est,si je comprends bien, fournie par un capteur. On calcule alors l'ordonnée correspondante.
Ensuite tout dépend de la spécification du problème et de la façon d'acquérir les données par le capteur.
Il peut s'avérer nécessaire de mémoriser les coefficients a et b dans deux tableaux a[i] et b[i].
A l'arrivée d'une mesure MesX fournie par le capteur, il faudra peut-être faire une recherche de l'indice i de la zone d'abscisses correspondante pour pouvoir calculer MesLink.
Bonsoir.
Merci pour vos explications , je comprends déjà beaucoup mieux la logique.
Voici comment j'ai commencé :
Procédure linéariser
Tableau réel Tab X
Tableau entier Tab Y
Var réel a,b
Var entier nb-mesure
Début
Lire (« Entrez nombre de mesure » ;nb-mesure)
Faire ....
Le but serait de faire calculer le coefficient directeur et l'ordonnée à l'origine pour chaque ligne.
Cette opération est a effectuer en fonction du nombre de mesure que l'on possède, c'est bien cela?
Comment commencer a programmer ma boucle?
Désolé je suis un peu lente mais c'est la première que j'utilise ces notions....
Merci pour votre aide !
Cordialement
Le problème est aussi que l'énoncé n'est pas très précis. On ne dit pas quand sont fournies les valeurs MesX. A l'avance ? En sachant qu'on est dans l'intervalle x(i), x(i+1) ? ou plutôt, ce qui correspondrait mieux à un processus expérimental, en temps réel, auquel cas, le capteur ayant fournit la valeur, on doit trouver dans quel intervalle on est pour x, donc trouver la valeur de i (algorithme de recherche). Une spécification précise du problème posé est indispensable en informatique.
La figure suggère qu'on commence à x(0). Il est dit explicitement qu'il y a 11 segments. Sauf que l'énoncé est faux, il fournit bien 11 coordonnées, mais cela ne définit que 10 segments ... Les problèmes d'intervalles niveau école élémentaire ... On s'arrête donc à x(10). Il y a par conséquent 10 valeurs des coefficients a et b. Je suggère donc de commencer par calculer et mémoriser ces valeurs dans deux tableaux:
Procédure linéariser
Tableau réel x {de 0 à 10}
Tableau réel y {de 0 à 10}
Tableaux réels a,b {de 1 à 10}
Var entier nb-mesure
Var réels, MesX, MesLink
{calcul et mémorisation des coefficients des segments}
i parcourant 0 ... 10
a(i) reçoit (y(i+1) - y(i))/(x(i+1) - x(i))
b(i) reçoit y(i) - a(i)x(i)
{traitement des mesures}
Lire (« Entrez nombre de mesure » ;nb-mesure)
j parcourant 1 ... nb-mesure
Acquérir_Capteur(MesX)
{recherche de l'intervalle contenant MesX, on suppose que le capteur ne mesure que dans l'un des 10 intervalles}
k reçoit 0
tant que MesX > x(k) : k reçoit k+1
{MesX est dans x(k-1), x(k)}
p reçoit k-1
MesLink reçoit a(p)*MesX + b(p)
Bonsoir,
Désolé pour ma réponse tardive.
J'ai bien compris la démarche que vous me proposez, cependant j'ai encore quelques questions :
Pour écrire mon programme en pseudo-code, j'ai appris que la variable tableau se déclaré de la maniàre suivante Tab (l, n ) avec l=ligne et n=colonne.
Soit est-il possible d'écrire au début de mon pseudo-code :
Procédure linéariser
Tab Réel x,y (10,2)
Tab Réel a,b (9,2) (pour le nombre de colonne, faut-il compter le 0 ? )
Ensuite, dans le cas ou nos mesures sont déjà données ( on ne fait pas l'acquisition au fur et à mesure mais bien à partir de données que l'on possède déjà, ici donc 11points) est -il necessaire de déclarer une variable nb-mesures?
Enfin, est-il possible de mettre en place ce programme a travers un seul pseudo code (sans phase de mémorisation des segments)?
Je vous remercie d'avance pour votre aide...
Cordialement,
Pour le pseudo-code, je suis incompétent 
Je veux dire, ensuite, code, pseudo-code, c'est de la syntaxe, je ne connais pas celle du pseudo-code que vous utilisez. Mais il faut bien sûr compter le 0, donc ça me semble être plutôt:
Tab Réel x,y (11,2)
Tab Réel a,b (10,2)
Si les mesures pour MesX sont fournies à l'avance (un autre tableau, peut-être, ou une lecture pour chaque intervalle, en sachant que la mesure est entre x(i) et x(i+1)), on peut effectivement tout rassembler en une seule boucle (programme proposé dans ma toute première réponse).
Bonsoir,
Voici , enfin ^^, le pseudo code :
Procédure Linéariser
Var réel tabX (i)
Var réel tabY (i)
Var entier nb-mesure
Début
Afficher("entrez le nombre de mesures")
Lire nb-mesure
i=0
Faire
a(i) = (TabY(i+1)-TabY(i))/(TabX(i+1)-TabX(i))
b(i) = TabY(i)-a(i)TabX(i)
Afficher ( "MeslinX"(i) "=" a(i)"MesX"(i) "+" b(i) )
Ligne suivante
Jusqu'à i= nb-mesure - 1
Fin
Voila qu'en pensez-vous?
Merci encore pour votre aide. Bonne soirée
Cordialement



 autre en post-bac
autre en post-bac