Bonjour,

Une bonne idée pour commencer : jeter un coup d'œil à ce que dit Sine qua non



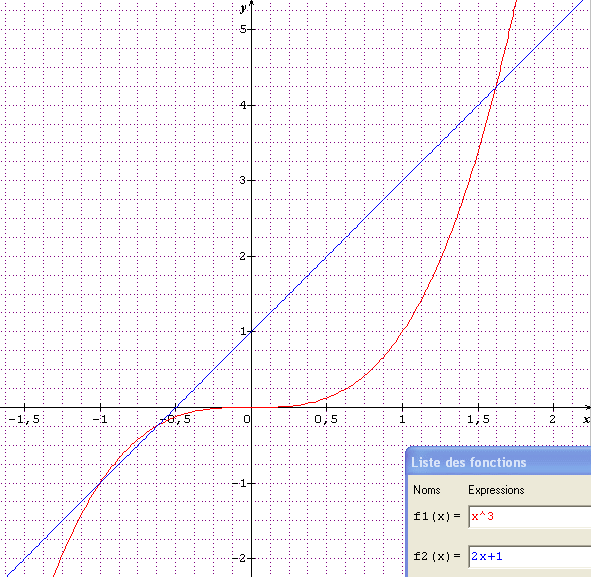
Cela donne déjà quelques réponses...

vous ne pouvez pas m'en dire un peu plus...car là effectivement représentation graphique des fonctions mais mon interprétation nulle!!!

Je peux en effet poser des questions.

Si x³ = 2x + 1 alors les courbes représentatives des fonctions
y = x³
et
y = 2x + 1
se coupent (pour une même valeur de l'abscisse x les ordonnées sont égales)

Donc... combien y a-t-il de solutions ?
Quelles sont les valeurs approchées de ces solutions ?

Cela aurait été bien de poster tout l'énoncé.
On ne devrait jamais commencer un problème sans l'avoir bien lu et relu plusieurs fois en entier. Cela aide beaucoup à la compréhension et à la recherche de la résolution.

donc je commence par le début énoncé du problème
avec un tableur
a) réaliser cette feuille de calcul et donner un encadrement d'une solution au problème (feuille de calcul comme expliqué auparavant valeur de x pour 0,1,2,3,4,5 et compléter les valeurs pour x3, 2x+1 et x3-(2x+1)
b) modifier la feuille de calcul de façon à donner une valeur approchée de la solution à 0.1 près puis à 0.01 et 0.001 près.
En quoi cette méthode est elle algorithmique

avec la calculatrice (ti 82)
a) utiliser la calculatrice pour conjecturer le nombre de solutions positives de l'équation x3=2x+1 (ajuster éventuellement la fenêtre graphique)
b) lire une valeur approchée de chaque solution.

je laisse le calcul formel...et le calcul algébrique ce serait trop long! merci

As-tu fait les quatre petits tableaux avec le tableur ?
Où en es-tu ? Tu as écrit en effet :

Pour le tableau je l'ai fait mais je n'ai pas utilisé de formule pour x3 et 2x +1 mais j'ai trouvé les valeurs (facile lol) et pour x3 - (2x+1) j'ai mis la formule correspondante qui est bien sûr colone x3 - colone 2x+1...
Quant aux valeurs approchées, j'ai mon idée mais elle me paraît trop simple, utiliser format cellule et modifier le nbre décimal...ça doit pas être ça!
Je ne comprends pas la démarche certainement!

Il y a toujours de très nombreuses manières de faire.

Voici ce que j'ai fait faire à mon tableur :



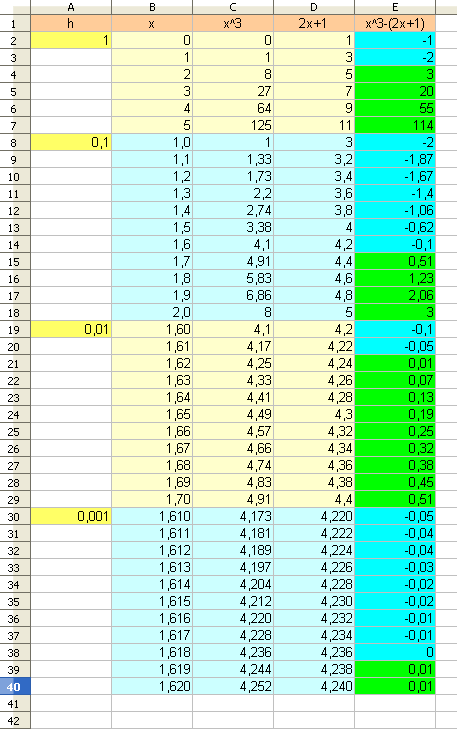
Dans la colonne E j'ai demandé que les valeurs négatives ou nulles soient sur un fond bleu et que les valeurs positives soient sur un fond vert. Cela aide bien à répondre aux questions.

Mais tu ne réponds à aucune de mes questions...

je ne réponds pas aux questions...parce que je n'ai pas de réponse ...que des questions et pour cause, je ne comprends pas le but de l'algorithme.... d'ailleurs en quoi cette méthode est-elle agorithmique?
Merci quand même de votre aide, je ne voudrais pas abuser de votre patience.

Avec
. ce que j'ai déjà écrit
. le graphique
. le tableau

il est très facile de répondre à plusieurs questions de l'exercice.

A toi !

A la question "peut-on trouver un réel positif etc...." par rapport au tableau pour x = 1.618 ....par contre graphiquement nous avons 3 points d'intersection...est ce que cela prouve que c'est algorithmique?

Il y a trois solutions, deux négatives et une positive qui vaut en effet environ 1,618

Procédé algorithmique : démarche mathématique et logique, régulière et mécanisable.

Il ne serait pas trop difficile de rédiger une "macro" pour que le tableur trouve tout seul la solution à une approximation donnée.
Il serait facile (je le ferai peut-être ce soir) de programmer par exemple Algobox avec un petit programme qui trouverait lui aussi la solution automatiquement.

Or mon ordinateur n'a jamais été à l'école et n'a jamais appris l'algèbre. Mais il peut trouver la solution grâce à un procédé algorithmique !

oui j'ai bien vu qu'il y avait ce logiciel de dispo à télécharger...mais l'exercice ne précise pas quel tableur utilisé est ce qu'avec open office (je n'ai que celui ci à disposition et en plus par aussi top qu'excel) on peut effectuer ce genre de calcul?
je n'ai pas dû "à mon époque" faire de l'algorithme et heureusement car je n'avais pas d'ordi! autant jusqu'ici j'arrivais à suivre mais là ça commence à devenir difficile!
merci pour tout...mon fils va prendre le relais et essayer de comprendre en fonction de vos infos très utiles.

Je n'ai pas non plus Excel. Ce que j'ai posté à 15 h 20 a été fait avec Calc d'Open Office.

Voici, sans prétention, un petit programme fait avec Algobox (excellent petit logiciel gratuit) :

1   VARIABLES
2     i EST_DU_TYPE NOMBRE
3     h EST_DU_TYPE NOMBRE
4     x EST_DU_TYPE NOMBRE
5   DEBUT_ALGORITHME
6     x PREND_LA_VALEUR 0
7     h PREND_LA_VALEUR 1
8     POUR i ALLANT_DE 1 A 4
9       DEBUT_POUR
10      TANT_QUE (x*x*x<2*x+1) FAIRE
11        DEBUT_TANT_QUE
12        x PREND_LA_VALEUR x+h
13        FIN_TANT_QUE
14      x PREND_LA_VALEUR x-h
15      AFFICHER x
16      h PREND_LA_VALEUR h/10
17      FIN_POUR
18  FIN_ALGORITHME

et voici, quand on le lance, ce qu'affiche l'écran :



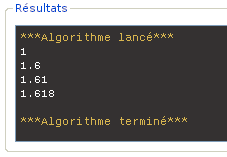
La méthode proposée est donc bien un procédé algorithmique...

Bonjour,
Désolé de vous déranger encore pour ce DM, mais aujourd'hui je dois faire le même devoir maison avec juste quelque questions en moins. J'ai quelque point qu'il faudrait m'éclaircire.
Comme:

"donner un encadrement d'une solution au problème"

Je ne comprends pas le sens de la phrase, pourriez vous me l'expliquer avant demain ???! Merci beaucoup !

:?

Pourriez-vous aussi faire une fiche de mathématiques sur les algorithmes ???! Je vous en serait très reconnaissante.