Inscription / Connexion Nouveau Sujet
Amortissement d’une dette
Bonsoir,
Pouvez vous m'aider à faire cet exercice s'il vous plaît :
Pour financer l'achat d'une voiture, un couple emprunte un capital de 20.000 €,
avec des mensualités de remboursement constantes égales à 500 €
Sa banque lui propose un taux annuel d'emprunt de 3,84 %, soit un taux mensuel de 0 32 %.
Chaque mois, la mensualité de 500 € se répartit entre des intérêts (0,32 % du capital restant dû en début de
mois) et un remboursement du capital.
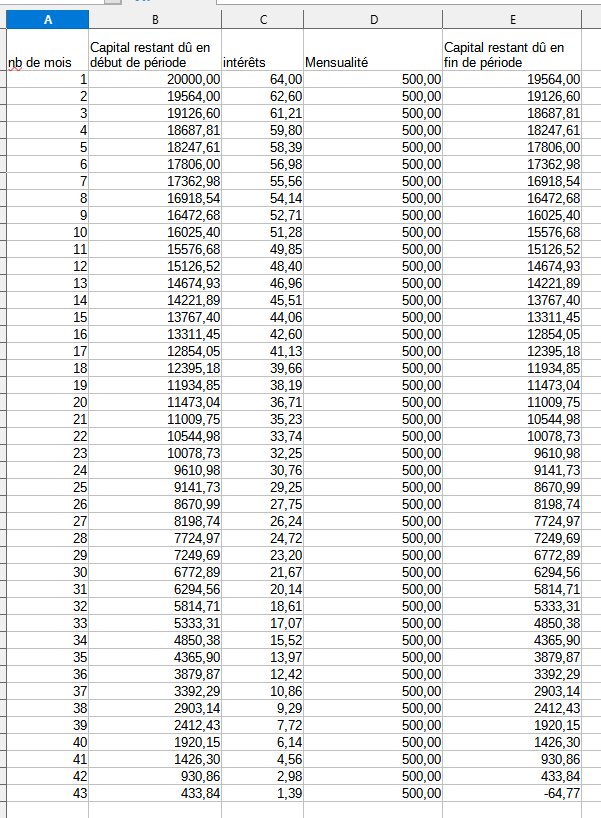
1) Justifier que les intérêts du premier mois s'élèvent à 64 € et que le capital restant dû à l'issue du premier mois est égal à 19 564 €
2) Calculer les intérêts du 2e mois et le capital restant dû à l'issue de deux mois de remboursement.
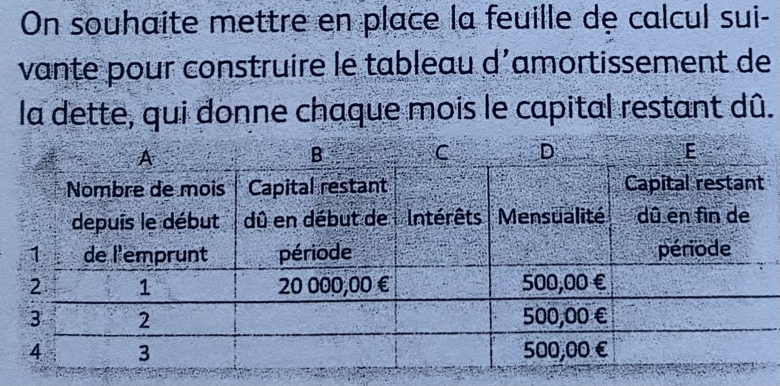
3) Proposer des formules à entrer dans les cellules €2, E2 et B3, à recopier vers le bas, de façon à construire le tableau d'amortissement.
4) 4. a. Après combien de mois sera remboursé le prêt ?
Quel sera le montant de la dernière mensualité ?
b. À l'aide du tableur, calculer le coût du prêt, c'est-
à-dire le montant que le couple verse à sa banque
en plus du montant emprunté. Quelle proportion du
montant emprunté celui-ci reprêsente-il?
Merci beaucoup
Bonjour à vous deux,
en attendant le retour de malou :
la question 1 ne devrait pas te gêner : "justifier que les interets s'elèvent à 64 euros...
"
taux d'interet de 0,32%,
le capital restant dû au départ = 20000 euros
il faut poser un calcul...
tu me poses la question ?
Oui, bien sûr, c'est ça.
appliquer un pourcentage à une somme, tu le fais depuis la 5ème, n'est ce pas ?
quel est alors le capital restant dû à l'issue de ce premier mois ?
oui, mais comprends tu ce que tu écris ?
nouveau capital = 20000 - (500 - 64) correspond à
nouveau capital = ancien capital - (echeance - interets).
on enlève au capital la part de l'échéance qui correspond au remboursement de capital.
Echéance = 500 si les interets sont de 64, on rembourse (500-64)=436 euros de capital.
OK ?
A présent, réponds à la question 2.
Ok!
Alors pour la 2) je fais 19 564*0,32 = 62 60,48/100 = 62 6048 €
Et pour le capital : 19 564-500+62,6048 = 19 126,6048 ?
oui,
mais ce sont des euros ! 62,6048 euros, c'est impossible. IL faut arrondir au centième d'euros.
interets = 62,60 euros
capital restant dû = 19 126,60 euros
question 3 :
que vas tu mettre comme formule de calcul ?
C2 : OK
E2 : capital - echeance + interets
tu ne peux pas mettre 64 puisque tu as vu qu'en période 2, les interets ne valent pas 64, ils sont recalculés à chaque ligne.
Les interets ne sont pas constants.
B3 : le capital en début de mois, c'est le capital à la fin du mois précedent..
E2 : ne mets pas de montant dans tes formules !
Si demain on te dit "que serait l'impact si la mensualité passe à 600 euros ?" par exemple, tes formules ne sont plus bonnes.
en E2 : = B2 - D2 + C2 ( tu as mis les interets en C2, pourquoi les recalculer ?).
Ainsi, en E2, on a le capital à la fin de la période, qu'on veut reporter comme capital restant dû en début de période suivante ==> .
en B3 : =E2
NB : Quand tu décides de ne plus répondre, comme hier soir, dis le, ça évite de t'attendre. OK ?
Pour la prochaine question, je compte utiliser un tableur vers 16h car je finirai les cours à ce moment là
J'ai mis toute mes données sur un tableur. Mais je ne sais pas où regarder pour voir à quel moment est remboursé le prêt…
tu as rempli la première ligne avec ce que tu avais dans l'énoncé ?
tu as mis une colonne avec le n° d'échéance ?
tu as placé les bonnes formules en C2, E2, B3 ?
tu as tout tiré vers le bas ?
ton tableau calcule tous les capitaux restant dûs ?
montre moi !
Oui j'ai tout mis sauf que quand je décide de vous envoyer la taille du fichier ça affiche qu'elle est trop grosse…
Je vous enverrai cela ce soir car je n'ai actuellement pas mon ordinateur, je l'ai prêté à un de mes camarades.
Si vous le voulez bien, on verra donc la question 3 et 4 tout à l'heure.
Pouvez vous maintenant, si vous le voulez, m'aider pour la parti B
Je vous donne l'énoncé :
Pour tout entier n>0, on note C, le capital restant
dû à la fin du nième mois de remboursement du prêt
et I. les intérêts du nième mois de remboursement.
Ainsi C, = 20000 ; C, =19564 ; I = O et I,=64.
1. Justifier que, pour tout entier naturel n, on a :
Cn+1 =1,0032x C,-500
2. a. Montrer que la suite (un) définie sur N par
Un =Cn- 156 250 est géométrique. Préciser sa raison.
b. En déduire l'expression de Cn en fonction de n.
c. À l'aide de la calculatrice, résoudre dans N l'inéquation Cn ≤0. Interpréter le résultat obtenu.
3. «. Justifier que, pour tout entier n > 1, on a :
In=0,0032 x Cn-1
b. En déduire que, pour tout entier n >1:
In= 500-436 × 1,00321n-1
4. Calculer la somme I1+ I2 +… + I44. Interpréter |e résultat obtenu
Pour l'instant j'ai fait la question 1 : une augmentation de 0,32% se traduit par une
multiplication par 1,0032*C et un remboursement de 500euros par mois par une soustraction de 500, soit le mois suivant Cn+1=1,0032*Cn-500.
Je bloque pour la suivante
messages croisés.
A l'avenir, présente ton énoncé complet dès le départ.
"C, = 20000 ; C, =19564 ; I = O et I,=64".
que sont les virgules ?
n'est ce pas plutôt
C0 = 20000 ; C1 =19564 ; I0 = O et I1=64 ??
Q1 : Cn+1=1,0032*Cn-500 oui
Q2 : Un =Cn- 156 250
Si la suite (Un) est géométrique, elle s'écrit Un+1 = q* Un
exprime Un+1 ...
Promis je répondrais !! On finit ce soir même s'il faut rester jusqu'à 00h
Moi, je n'ai pas prévu de rester sur ce devoir jusque minuit !!
"Un+1 = (Cn+1)+q " : ??
Un =Cn - 156 250
Un+1 =Cn+1 - 156 250
remplace Cn+1 par son expression en fonction de Cn
andredilute78, en terminale, tu devrais faire plus attention !
quand tu divises 156750 par 1,0032, tu trouves 500 ?
OK pour le tableau.
Sur la dernière échéance, en ligne 43, tu ne dois pas payer 500,
il reste moins que ça.
La derniere échéance vaut 435,23 euros, et le capital est alors totalement remboursé.
43 433,84 € 1,39 € 435,23 € 0,00 €
Merci @heckla !
Ah d'accord, je n'avais pas trop compris vos explications. Bien évidement il faut que je développe
Un+1 = 1,0032(Cn-157 251,6)
C'est ça?
il n'y a rien à comprendre.. tu le fais depuis la 4ème.
8x - 24 = 8 ( x - 3) pour trouver 3, on a divisé 24 par 8
ainsi, quand on re-développe, on a bien 8*x - 8*3
si je mets 8 en facteur, je divise chaque terme par 8
8x / 8 donne x
24/8 donne 3
d'ou 8(x-3)
ici tu mets 1,0032 en facteur, donc...
ouf !
donc Un+1 = 1,0032( Cn - 156250)
et Cn - 156250 c'est Un
donc
Un+1 = 1,0032 Un ==> suite géométrique de raison q=1,0032
je te laisse calculer U0, dont on va avoir besoin
U0 = C0 - 156250 ...
b. En déduire l'expression de Cn en fonction de n.
écris d'abord l'expression de Un en fonction de n
Un= Uo*q^n
Un= -136 250*1,0032^n ?
OK, tu sais que Un = Cn -156250
donc Cn = Un + 156250
et maintenant tu as Un en fonction de n, donc Cn = ?
en effet, je t'ai écrit que Cn= Un+ 156 250
tu sais que Un = -136 250*1,0032^n
donc Cn = -136 250*1,0032^n + 156250
c. À l'aide de la calculatrice, résoudre dans N l'inéquation Cn ≤0. Interpréter le résultat obtenu.
Cn <= 0
-136 250*1,0032^n + 156250 <= 0
-136 250*1,0032^n <= - 156250
1, 0032 ^n >= 156250/136250
comment fais tu pour trouver n, à ce stade ?
soit, tu passes par les logarithmes (Ln), mais si tu ne les as pas vus, tu fais des essais avec ta calculatrice.
Aide toi de ton tableau :
Cn >=0 correspond à "le capital restant dû n'est plus positif".
On a vu sur le tableau que ça correspond à n=43.
Q3 : justifier que Justifier que In=0,0032 x Cn-1
c'est évident : pour calculer les interets d'une période, on multiplie le capital restant dû en fin de période précédente par le taux.
b. En déduire que, pour tout entier n >1:
In= 500-436 × 1,00321n-1
corrige ton énoncé, et vas y !
C'est encore une fois la même démarche :
In=0,0032 x Cn-1
remplace Cn-1 par son expression en fonction de n