Niveau école ingénieur

Analyse à composante principal (ACP)

Posté par
toureissa 13-06-21 à 01:20

Bonsoir à tous,

J'ai un souci avec l'analyse à composante principal et j'aurais besoin de votre aide.

On a p variables quantitatives observées sur n individus. On cherche à représenter le nuage des points des individus. À chaque individu on peut associer un point de R^p . Il est impossible de visualiser le nuage dès que p>3.

On cherche alors une représentation des n individus dans un sous-espace F_k de R^p de dimension k (par exemple un plan). Autrement, on cherche à définir k nouvelles variables combinaison linéaires des p variables initiales qui ferons perdre le moins d'information possibles.
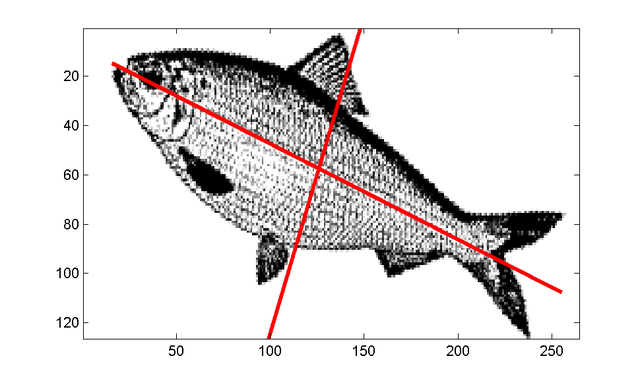
L'image ci-dessous de la poisson résume l'objectif de l'ACP.

Cependant je n'arrive pas à comprendre ceci:

Fk devra être «ajustee» le mieux possible au nuage des individus :la Somme des carrés des distances des individus à Fk doit être minimale

équivalent à :

Fk est le sous-espace tel que le nuage projeté ait une inertie (dispersion) maximale.

Analyse à composante principal (ACP)

Posté par re : Analyse à composante principal (ACP) 18-06-21 à 18:41

Je vous livre une explication dans le plan mais ceci est généralisable en dimension $d$ . En espérant que
ceci apporte un éclairage utile.

Les   $N$ pixels de l'image sont distribués dans le plan $\mathbb R^2$ . A chaque pixel $(i)$ est associé
une position   $(x_i,y_i)$ rapportée aux axes coordonnés.
On peut estimer le centroïde (ou l'espérance) de cette distribution comme la position moyenne (\bar x, \bar y).

$\bar x = 1/N \sum_i x_i$    $\bar y = 1/N \sum_i x_i$

On peut estimer la matrice carrée de variance-covariance encore appelée tenseur d'inertie de cette distribution de taille 2x2 ,  symétrique de la forme,

$\begin{pmatrix}I_xx &Ixy \\ Iyx=Ixy & I_yy\end{pmatrix}$

avec

$I_{xx} =1/N \sum_{i=1}^{N} (x_i - \bar x)(x_i-\bar x)$

$I_{yy} =1/N \sum_{i=1} ^{N}(y_i - \bar y)(y_i-\bar y)$

$I_{xx} =1/N \sum_{i=1}^{N}\n (x_i - \bar x)(x_i-\bar x)$

$I_{xy} =1/N \sum_{i=1}^{N}\n (x_i - \bar x)(y_i-\bar y)$

L'analyse ACP n'est rien d'autre que la diagonalisation de cette matrice.  Un vecteur propre issu de cette diagonalisation oriente un axe principal du tenseur d'inertie c'est à dire le sous-espace propre du plan qui maximise la dispersion des points de la distribution  relativement à son sous-espace orthogonal complémentaire (c'est à dire la somme des carrés de la projection orthogonale des points sur ce sous-espace complémentaire) ce qui revient à dire qu'un axe propre donné représente aux mieux  la direction selon  laquelle la dispersion des points relativement au sous-espace propre qui lui est orthogonal est maximal.

En passant de la base initiale dans  la base propre ACP, le tenseur d'inertie admet une représentation diagonale de la forme,

$\begin{pmatrix}\lambda_1 & 0\\ 0 & \lambda_2\end{pmatrix} \\$
où les valeurs propres   $\lambda_1$   et $\lambda_2$   mesurent chacune la dispersion de la distribution de points relativement au sous-espace orthogonal à l' espace propre qui leur est associée .

En dimension 2 elles déterminent les demi-grands axes d'une ellipse de dispersion centrée sur le centroïde. Leur somme c'est à dire la trace du tenseur d'inertie $I_xx+I_yy$ mesure la dispersion totale.  Elle est  conservée dans l'analyse  PCA. donc égale à $\lambda_1 +\lambda_2$ mais le couple $\lambda_1 +\lambda_2$   maximise, nous l'avons vu, les dispersions des points sur relativement à leur sous-espace orthogonal.

Les relations linéaires évoquées sont simplement celle du changement de la base orthogonal unitaire (i.e. de la rotation)
menant de la base initiale à la base PCA.