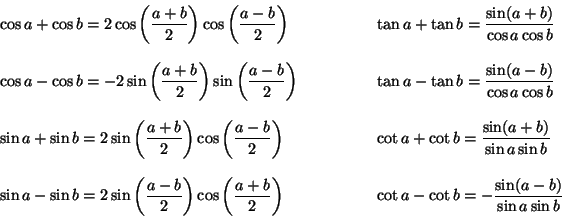
Bonsoir,

ça en fait des formules!!

commence par diviser ton équation par 2
et remplace alors 1/2 par cos(/3 et (3)/2 par sin(/3)

ensuite utilise la formule de cos(a+b)

BONSOIR,
Je divise toute l'équation par deux?
  cosx - 3 sinx = 2 cos ( x+ /3) donc ça donne si je ne me trompe pas :

  1/2cosx - (sin/3) sinx = 1/2 cos x. ?
  

euh...

  cos ( x + 1/2) plutot, pour le second membre?

en divisant tout par 2 on a :

(1/2)cosx - (3/2)sinx = cos(x + /3)

tu obtiens  :

cos(/3)cosx - sin(/3)sinx = cos(x + /3)

A donc je touche pas au second membre, enfin sauf (pour la division par 2)
Je travaille que sur le premier ...
Mais cos(a+b)= cos a x cos b - sin a x sin b.
Tu fais pas l'inverse la, ou c'est pas grave?
mais je commence à comprendre ... merci

Ah oui si c la même chose c'est une multiplication ... j'ai un peu de mal. Merci beaucoup

cos(/3)cosx - sin(/3)sinx = cos(x + /3)

le 1er membre est bien de la forme cos(a+b)

En déduire les solutions de cosx- 3 sin x = 1

Donc on trouve quand on divise par deux que ça équivaut à :

cos (/3) cos x - sin(/3 sinx = 1/2

cos ( /3 + x ) = 1/2 ?

cos 1/2 = /3

{cos ( x + /3) = /3 [2]
ou x= 2/3 [2].

et je fais la même chose pour cos -1/2 = 2/3)
On aura deux solutions?
c'est bon?

cos(/3+x) = cos(/3)

donc /3+x = /3 + 2k, k
/3+x = -/3 + 2k', k'

et tu résous

donc si je résous, j'en arrive à :

  x = 2k et x= -2/3 + 2k' ?

maintenant tu dois donner toutes les solutions dans l'intervalle qu'on t'as fixé pour la résolution

Ah ok ok ... et bin heureusement qu'il y a ce site. Merci ça m'a beaucoup aidé. Je vais retravailler sur ce genre d'exercice. Bonne soirée et encore merci.
A biento surement!!